Понятие о деформациях и напряжениях
Воздействие на тело внешних сил изменяет его внутренние силы. Деформация тела вызывает изменение расстояний между атомами, при этом возникающие дополнительные внутренние силы стремятся вернуть тело в первоначальное положение. Если неограниченно увеличивать действие внешних сил, то при определенном возрастании внутренних сил происходит разрушение тела. Чтобы произвести расчет на прочность, надо уметь определять внутренние силы, зная внешние. Для определения внутренних сил (или внутренних силовых факторов) используют метод сечения. Мысленно рассекаем твердое тело и отбрасываем одну из частей. Оставшаяся часть тела находится в положении равновесия под действием приложенных внешних сил и сил, приложенных к сечению (заменяющих воздействие отброшенной части тела). Теперь при помощи теоретической физики можно определить главный вектор действия внутренних сил по сечению (закон распределения этих сил установить сложно). Совмещая плоскость сечения с системой координат, имеем в сечении шесть силовых факторов: продольная сила Nz, пара поперечных сил Qx,Qy, изгибающие моменты Mx,My, крутящий момент Mz.
Соответственно видам внутренних силовых факторов различают четыре вида деформаций тела:
– если в сечении имеется только продольная сила – растяжение или сжатие;
– если в сечении возникают только поперечные силы – сдвиг;
– если в сечении возникают только изгибающие моменты – чистый изгиб, если кроме изгибающих моментов возникают поперечные силы – поперечный изгиб;
– если в сечении возникает крутящий момент – кручение.
Если в сечении действуют несколько силовых факторов, то возникает сложный вид деформации.
Как уже было сказано, при определении внутренних сил методом сечения считаем эти силы приложенными к центру тяжести сечения. На самом деле они распределены по всей поверхности сечения, и интенсивность внутренних силовых факторов может быть различной. Увеличение внешней нагрузки приводит к увеличению внутренней, заставляет возрастать интенсивность во всех точках сечения и может привести к разрушению элемента или возникновению остаточных деформаций. Таким образом, говоря о прочности тела, рассматривать надо не значение внутренних сил, а их интенсивность. Меру интенсивности внутренних сил характеризует напряжение. Для удобства математического и физического анализа напряжение рассматривают как совокупность двух компонент: вектора нормального напряжения и вектора касательно напряжения, являющихся соответственно его составляющими по нормали к сечению и касательно к его плоскости.
Нагрузки (наружные силы).
Если повнимательнее присмотреться к рисунку 1, то можно увидеть, что линейка немного прогнулась посредине. Если взять более длинную 40-сантиметровую линейку и опереть ее на книги, то прогиб посредине линейки будет еще более заметным, но все равно пока не очень явным.
Почему же это случилось?
Оказывается, на линейку действует нагрузка — собственный вес линейки и под действием этой нагрузки линейка прогибается, при этом наибольший прогиб мы можем видеть посредине. Причем, чем больше расстояние между опорами — l, тем меньше несущая способность балки при одном и том же сечении и получается, что расчетная длина балки — очень важный фактор при расчетах. Так как линейка имеет простую параллелепипедную форму и плотность материала, из которого изготовлена линейка приблизительно одинаковая, то такая нагрузка считается равномерно распределенной и на расчетных схемах изображается так:
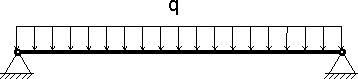
Рисунок 5.
2.1. Распределенная нагрузка может быть равномерной, как показано на рисунке 5, так и неравномерно распределенной, при этом значение распределенной нагрузки может изменяться линейно и не линейно, кроме того распределенная нагрузка может действовать не на всю длину балки, а на один или несколько участков. Если на балку действует несколько равномерно распределенных нагрузок, например: собственный вес, вес от кирпичной кладки, опирающейся на балку, и нагрузка от плит перекрытия то такие распределенные нагрузки можно суммировать, что в дальнейшем значительно облегчает расчеты. Подобный подход называется принципом суперпозиции.
2.2. Если у Вас есть палец, а я думаю, таковых у Вас имеется немало, то при надавливании пальцем на середину линейки линейка прогнется уже значительно заметнее. В этом случае на линейку действует кроме равномерно распределенной нагрузки еще и сосредоточенная (точечная) нагрузка (на рисунке 6 распределенная нагрузка не показана):

Рисунок 6.
Само собой точечных нагрузок может быть сколь угодно много и прикладываться они могут в любом месте балки и не только перпендикулярно оси балки, но и параллельно. Если сосредоточенная нагрузка приложена перпендикулярно на опоре, то на балку это никак не повлияет, просто возникнет реакция опоры численно равная нагрузке и направленная противоположно. Вы можете это легко проверить сами, надавив пальцем на линейку в месте опоры на одну из книг, если уж очень сильно давить, то Вы скорее промнете книгу, но линейка все равно не прогнется.
Почему так происходит?
Оказывается нагрузка, действуя на балку, создает изгибающий момент, т.е. хочет повернуть балку вокруг опор. При этом значение изгибающего момента напрямую зависит не только от величины нагрузки, но и от плеча действия силы. Нетрудно догадаться, что максимальный изгибающий возникает тогда, когда сосредоточенная нагрузка действует на балку посредине.
Конечно же действует этот момент на балку не просто так, а в рассматриваемом поперечном сечении балки и возникает он в данном случае от действия опорной реакции, которую еще следует определить, но об этом разговор пойдет дальше.
Иногда при расчетах вводится понятие вращающего момента, действующего на балку:
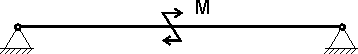
Рисунок 7.
Все, больше никаких вариантов нагрузок, действующих на балку, при решении задач по расчету строительных конструкций не рассматривается. Впрочем, классификация нагрузок — наружных сил — это отдельная большая тема.
Ну и теперь непосредственно сам сопромат, потому как до этого описывались термины и понятия теоретической механики.
Треугольное сечение
z
h 0 y
z
A b B
На рисунке показано треугольное сечение, для которого требуется определить момент инерции относительно оси АВ, совмещенной с основанием треугольника.
По определению
(1)
Из чертежа находим:
Подставляя значения dF в выражение (1) получим :
Окончательно
(2)
Устойчивость стержней (продольный изгиб)
Если стержень,( показанный на рис.1 ) сжимать силой, то при некоторой величине этой силы стержень из устойчивой прямолинейной формы перейдет в неустойчивую криволинейную (см. пунктир). Сила, при которой стержень начинает искривляться (деформироваться), называют критической или эйлеровой силой .
Pэ Р Рэ
Рис.1
Положение равновесия тела называют устойчивым, если, представленное самому себе после отклонения от этого положения, тело стремится вернуться в исходное положение (рис. 2)
Рис. 2
Положение тела называется неустойчивым, если тело, отклоненное от равновесного и предоставлено самому себе, откланяется от этого положения (рис. 3).
Рис. 3
Положение тел называется безразличным, если оно, откланяется от равновесного положения и представлено самому себе, остается на месте (рис. 4).
Рис. 4
Рассмотрим стержень, показанный на рисунке, и будем считать, что сила доведена до такой величины, что стержень искривляется (см. пунктир)
y
z
y
P z
l
В этом случае изгибающий момент в текущем сечении запишется в виде
. (1)
В дальнейшем (для простоты записи) будем считать:
, .
тогда:
. (1)
Дифференцируя дважды уравнение (1), получим:
Бизнес и финансы
БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством
Классификация сил
Любой элемент конструкции можно рассматривать как самостоятельный, если воздействие остальных элементов считать силами внешнего воздействия. К внешним силам относят как силы, действующие со стороны других элементов, так и реакции связей (опор). Действующую на тело систему сил принято называть нагрузкой.
Внешние силы принято делить на объемные, т. е. распределенные по всему объему, и поверхностные, действующие только на поверхность рассматриваемого элемента. Поверхностные силы в свою очередь подразделяются на сосредоточенные и распределенные по поверхности элемента или по длине элемента. Если сила передается на деталь по площадке, размеры которой пренебрежимо малы в сравнении с площадью всего элемента конструкции, силу считают сосредоточенной. Это упрощение служит для облегчения расчетов. Распределенные по поверхности нагрузки характеризуются давлением, т. е. отношением силы, действующей на элемент нормально к нему, к площади данного элемента. Распределенная по длине нагрузка характеризуется интенсивностью, выражаемой единицей силы, отнесенной к единице длины.
Сосредоточенные силы измеряются в ньютонах (H), распределенные по поверхности (давление) – в паскалях, распределенные по длине (интенсивность нагрузки q) – в ньютонах на метр (Н/м).
Также нагрузки подразделяются по характеру изменения во времени.
Статические нагрузки характеризуются постоянством во времени.
Динамические нагрузки, абсолютное значение, направление и место приложения которых изменяются во времени. Такие нагрузки могут быть кратковременными или действующими продолжительно и изменяющимися по какому-либо закону.
Укажем самые распространенные типы связи.
Односвязная опора (шарнирно-подвижная) изображена на Рис. 1.1. Реакция такой опоры всегда перпендикулярна опорной поверхности.
Двухсвязная опора (шарнирно-неподвижная) схематически изображена на Рис. 1.2.
Реакция этой опоры проходит через центр шарнира, ее направление зависит от действующих сил. Вместо отыскания числового значения и направления этой реакции удобнее найти две ее составляющие.
В трехсвязной опоре (жесткой заделке), изображенной на Рис. 1.3 возникают реактивная пара сил (момент) и реактивная сила, последнюю удобнее представлять в виде двух ее составляющих.
Рис. 1.1
Рис. 1.2
Рис. 1.3
Момент инерции
При исследовании вращения твердого тела физики часто пользуются понятием момента инерции.
Определение 2
Моментом инерции системы (материального тела) относительно оси вращения называется физическая величина, которая равна сумме произведений показателей точек системы на квадраты их расстояний до рассматриваемого вектора.
Суммирование производится по всем движущимся элементарным массам, на которые разбивается физическое тело. Если изначально известен момент инерции исследуемого предмета относительно проходящей через его центр масс оси, то весь процесс относительно любой другой параллельной линии определяется теоремой Штейнера.
Теорема Штейнера гласит: момент инерции вещества относительно вектора вращения равен моменту его изменения относительно параллельной оси, которая проходит через центр масс системы, полученному посредством произведения масс тела на квадрат расстояния между линиями.
При вращении абсолютно твердого тела вокруг неподвижного вектора каждая отдельная точка движется по окружности постоянного радиуса с определенной скоростью и внутренний импульс перпендикулярны этому радиусу.
.
Экспериментально установлено, что касательные напряжения, возникающие под действием внешних нагрузок в поперечных сечениях, при кручении круглого вала распределяются неравномерно. В центре вала значение касательного напряжения равно нулю. Двигаясь от центра по радиусу окружности к поверхности вала, значения касательных напряжений начинают возрастать и достигают свойх максимальных значений на его переферии (рис.1).
y
rmax
r=0
D z
Рис.1
Характер распределения касательных напряжений позволяет сделать вывод, что в центральной части круглого вала их значения пренебрежимо малы и целесообразно применять валы кольцевого сечения (трубчатые или полые) с удаленной сердцевиной.
y
rmax
rp
D d r=0 z
Для расчета максимальных касательных, значений допускаемых касательных напряжений справедливы выше приведенные формулы. Следует лишь вместо значений и для сплошного вала подставить их значения для кольцевого сечения:
;
,
где :
,
d — внутренний диаметр сечения, в см;
D — наружный диаметр сечения, в см.
Разность характеризует поправку к значениям для сплошного круглого сечения, вызванную наличием отверстия.
Кроме проверки валов при кручении на прочность в ответственных узлах машин и аппаратов необходимо проверить работу вала на жесткость при кручении. Жесткость вала при кручении оценивается по наибольшему относительному углу закручивания на единицу его длины. При этом значение угла закручивания не должно превышать допускаемой величины:
(2)
или
(3)
где :
— допускаемый относительный угол закручивания, рад/cм;
— допускаемый относительный угол закручивания, град/м.
рад/см;
град/м.
G — модуль сдвига; для стали 8,0 Мн/.
полярный момент инерции;
Л и т е р а т у р а
1.Федосьев материалов. — М.: Наука, 1986.
2.Кинасошвили материалов. — М.: Наука, 1975.
3., , Маслов механика. — М.: Высшая школа, 1989.
4.Ковалев механика. — М.: Высшая школа, !982.
5.Сборник задач по сопротивлению материалов. Под редакцией — М.: Наука, 1984.
В В Е Д Е Н И Е………………………………………………………………………………………………
Краткая история развития науки о сопротивлении материалов
Задачи и методы сопротивления материалов………………………….
Реальный объект и расчетная схема…………………………………………….
Элементы конструкций и машин……………………………………………………
Внешние силы…………………………………………………………………………………………
Понятие о деформациях, внутренних усилиях и упругости
Основные допущения, принимаемые в сопротивлении материалов
Моменты инерции плоских фигур. Общие положения и понятия
Моменты инерции и моменты сопротивления простейших фигур
Прямоугольное сечение……………………………………………………………………
Круглое сечение……………………………………………………………………………………
Устойчивость стержней (продольный изгиб)…………………………..
Вывод основного дифференциального уравнения продольного изгиба
Интегрирование дифференциального уравнения продольного изгиба
Пример: Определение критической нагрузки (силы) для балки, показанной на рис.1
Сложное сопротивление…………………………………………………………………..
Основные понятия………………………………………………………………………………
Совместное действие изгиба и растяжения (сжатия)…………..
Совместное действие изгиба и кручения…………………………………..
Косой изгиб…………………………………………………………………………………………….
Расчет на прочность и жесткость при кручении сплошных и полых валов
Л и т е р а т у р а……………………………………………………………………………………..
История развития[править]
Зарождение науки о сопротивлении материалов связано с именами Леонардо да Винчи и Галилео Галилея.
В г. английский ученый Р. Гук (—) установил закон деформирования упругих тел. Этот закон является основным в сопротивлении материалов. Быстрое развитие науки о сопротивлении материалов началось в конце XVIII века в связи с бурным развитием промышленности и транспорта. Значительный вклад в развитие науки о сопротивлении материалов сделан выдающимися учеными Бернулли, Сен-Венаном, Коши, Ламе и др., которые сформулировали основные допущения и дали некоторые расчетные уравнения.
Особо следует отметить замечательные исследования знаменитого ученого Л. Эйлера (XVIII в.), члена Петербургской Академии наук. Его работа, посвященная расчету сжатых стержней на устойчивость, актуальна и в настоящее время.
В XIX в. мировую известность приобрели работы русских ученых Д. И. Журавского, Х. С. Головина и др. Формулой Журавского для определения касательных напряжений при изгибе пользуются и современные инженеры. Важные и интересные исследования по расчету сжатых стержней на устойчивость выполнены в конце XIX в. Ф. С. Ясинским.
С начала XX в. роль русских ученых в науке о сопротивлении материалов ещё более возросла. Появились замечательные работы профессора И. Г. Бубнова, академика А. Н. Крылова и др. Метод Бубнова для решения сложных задач сопротивления материалов пользуется мировой известностью. Весьма большой вклад в развитие науки о сопротивлении материалов внес С. П. Тимошенко, автор первоклассных учебников и многочисленных научных работ по вопросам расчета сооружений на прочность, устойчивость и колебания.
В настоящее время работниками научно-исследовательских институтов и высшей школы созданы новые эффективные методы расчета деталей сложной формы, находящихся под воздействием различных нагрузок. Это работы Н. Н. Давиденкова по теории прочности, академика С. В. Серенсена по изучению прочности деталей, работающих при переменных нагрузках, академика А. Н. Динника — по устойчивости, В. З. Власова — по расчету тонкостенных стержней и оболочек. Важные исследования выполнены Ю. Н. Работновым, А. А. Ильюшиным, Э. И. Григолюком, В. В. Болотиным, А. Ф. Смирновым, В. И. Феодосьевым, Н. И. Безуховым, А. Р. Ржаницыным, С. Д. Пономаревым, И. И. Трапезиным и др.
Задачи сопротивления материалов
Твердые тела при воздействии на них с какой-либо силой могут изменять свою форму и размеры, т. е. деформироваться. Если после снятия нагрузки тело возвращает свое первоначальное состояние, то деформацию называют упругой. Если после снятия нагрузки тело остается деформированным, то говорят о пластической (остаточной) деформации.
На практике остаточные деформации, возникающие в элементах, говорят о нарушении нормальной работы конструкции. При создании машин и сооружений необходимо выбрать материал и размеры деталей таким образом, чтобы при воздействии внешних сил сооружения не подвергались разрушению и остаточной деформации, т. е. были достаточно прочными. Прочностью называют способность тел выдерживать воздействие внешних сил без разрушения и возникновения опасных последствий.
На практике все конструкции и сооружения испытывают на себе упругие деформации. Если при достижении некоторого критического значения внешних воздействий конструкция перестает нормально функционировать, хоть и обладает необходимой прочностью, то говорят о недостаточной жесткости такой конструкции. Следовательно, жесткость – это способность тела сопротивляться влиянию упругой деформации.
Также под воздействием внешних воздействий тела могут изменять свою форму и оставаться в таком положении. При проектировании необходимо подбирать размеры так, чтобы возникающие в элементах упругие перемещения не нарушали общей работы конструкции или сооружения. Способность тел сохранять устойчивое равновесие называют упругостью. Поэтому можно сказать, что основной задачей предмета «Сопротивление материалов» является расчет элементов конструкций и сооружений, обеспечивающий им прочность, жесткость и устойчивость.
Сопротивление материалов – расчетно-теоретическая дисциплина. Для определения внешних сил, действующих на элементы конструкций и детали машин в эксплуатации, используют методы теоретической механики, в основном статики, в которых рассматривается равновесие абсолютно твердого тела. Составляя уравнения равновесия, допустимо заменять одну систему сил другой, эквивалентной ей, переносить силы вдоль линии их действия или заменять силы их равнодействующими, но в некоторых случаях такие упрощения могут быть причиной ошибочных расчетов. Поэтому все основные положения сопротивления материалов подвергаются многократным экспериментальным исследованиям и дополнениям.
В некоторых случаях теоретический расчет оказывается настолько сложным, что приходится изготавливать модель проектируемой конструкции и подвергать ее испытаниям, чтобы получить данные о характере и величине деформаций.
Презентация на тему: » Лекция 1 Основные положения. Сопротивление материалов Сопротивление материалов – наука об инженерных методах расчета на прочность, жесткость и устойчивость.» — Транскрипт:
1
Лекция 1 Основные положения

2
Сопротивление материалов Сопротивление материалов – наука об инженерных методах расчета на прочность, жесткость и устойчивость деталей машин и элементов конструкций. Сопротивление материалов Математика Теоретическая механика Физика Математика Теоретическая механика Физика База расчетных методов. Теоретические основы эксперимента Теоретические основы гипотез Теоретические основы расчетов Теории- упругости, пластичности, ползучести Теории- упругости, пластичности, ползучести Детали машин Расчет конструкций Детали машин Расчет конструкций Теоретические дисциплины Научные дисциплины Инженерные дисциплины
3
Классификация элементов конструкций l d d
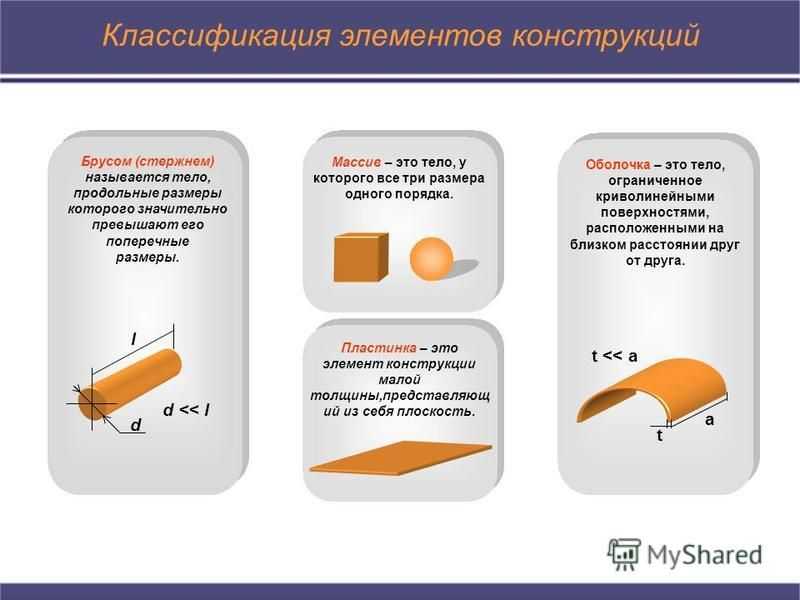
4
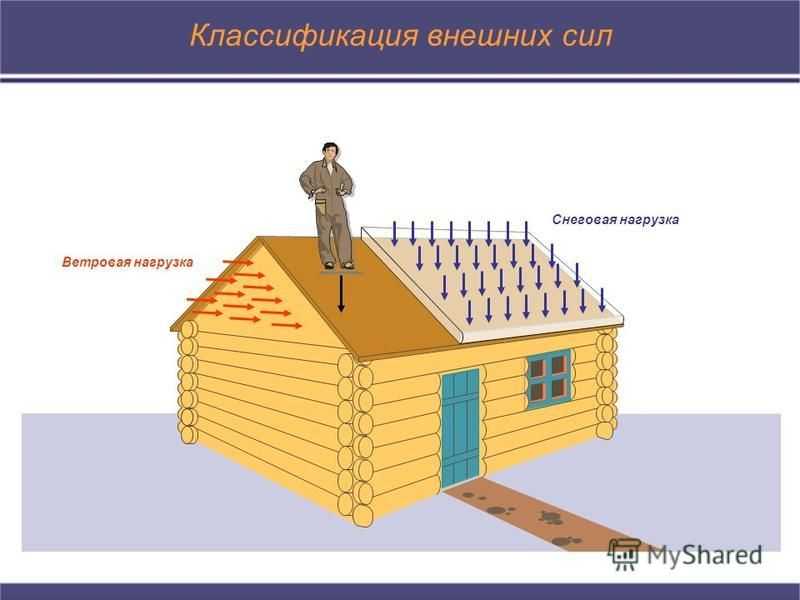
Классификация внешних сил Снеговая нагрузка Ветровая нагрузка
5
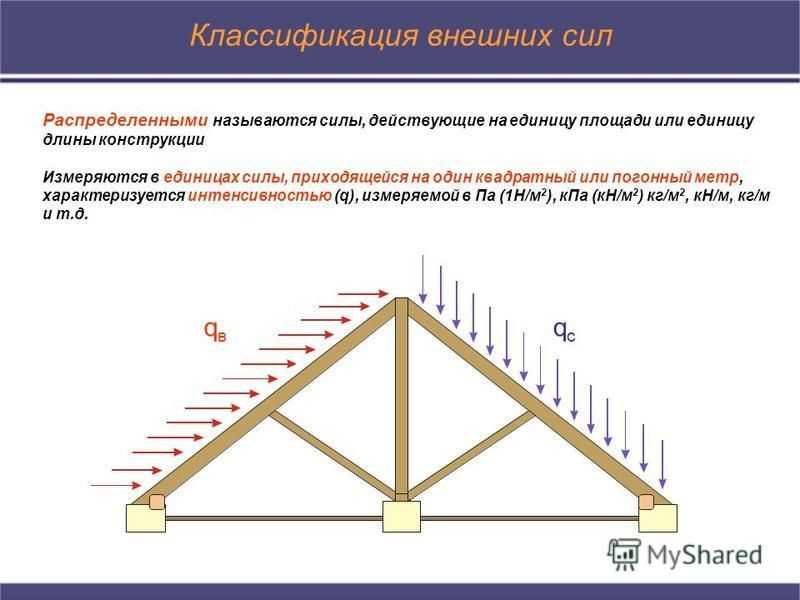
Классификация внешних сил Распределенными называются силы, действующие на единицу площади или единицу длины конструкции Измеряются в единицах силы, приходящейся на один квадратный или погонный метр, характеризуется интенсивностью (q), измеряемой в Па (1Н/м 2 ), к Па (кН/м 2 ) кг/м 2, кН/м, кг/м и т.д. qвqв qсqс
6
Понятие о деформациях. Виды деформации Изменение размеров и формы элементов конструкции при действии на них внешних сил называется деформацией. Упругими деформациями называют такие изменения размеров и формы, которые исчезают после удаления внешних сил. Деформация, не исчезающая после снятия внешней нагрузки, называется пластической или остаточной. Существует 4 вида деформации: 1. Растяжение или сжатие – возникает при работе канатов, тросов, колонн и др. 2. Сдвиг (перерезывание) – эту деформацию испытывают заклепки, сварные швы, шпонки, и др. 3. Кручение – эту деформацию испытывают валы, передающие мощность при вращательном движении. 4. Изгиб – на изгиб работают различные балки, оси, зубья, зубчатых колес и др.

7
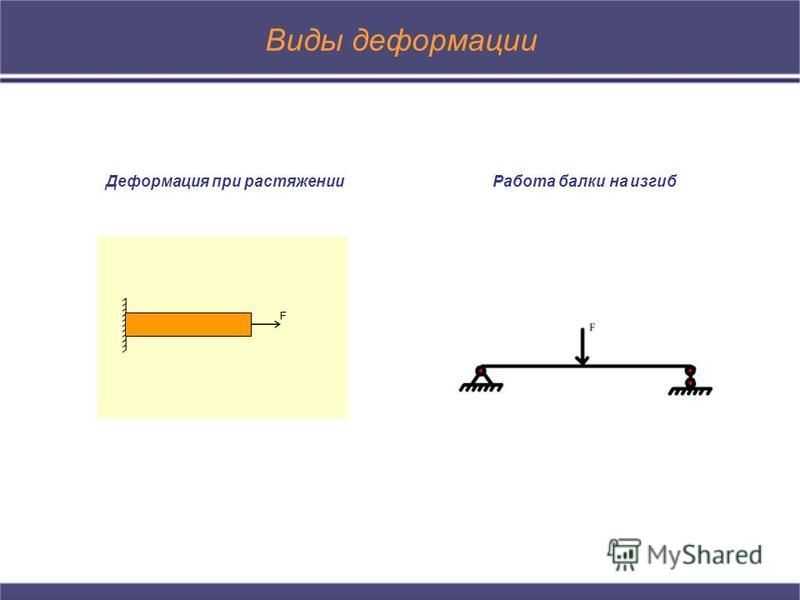
Виды деформации Деформация при растяжении Работа балки на изгиб
8
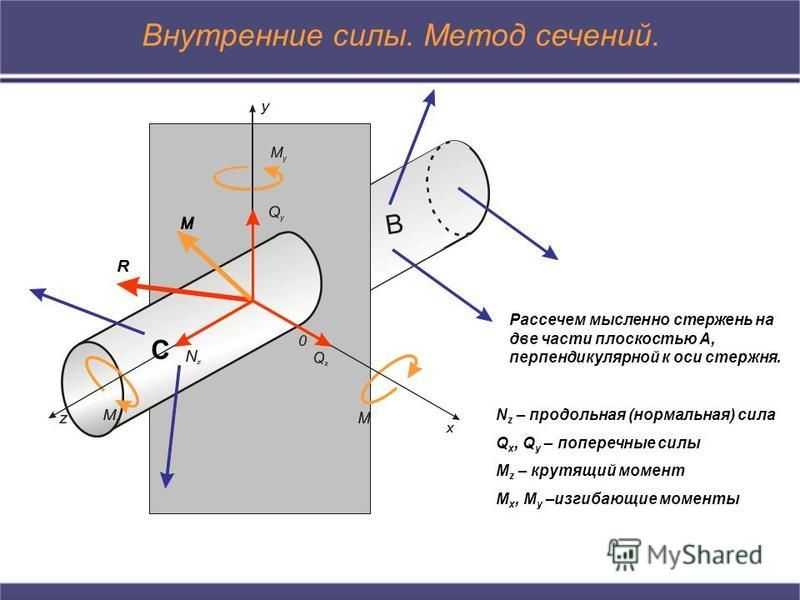
С Внутренние силы. Метод сечений. Рассечем мысленно стержень на две части плоскостью А, перпендикулярной к оси стержня. N z – продольная (нормальная) сила Q x, Q y – поперечные силы M z – крутящий момент M x, M y –изгибающие моменты
9
Понятие о напряжении Мера интенсивности внутренних сил, распределенных по площади сечения, называется напряжением Единица измерения Паскаль (1Па=1Н/м 2 ) Мегапаскаль (1Мпа=10 6 =Па) σ (сигма) – нормальное напряжение τ (тау) – касательное напряжение
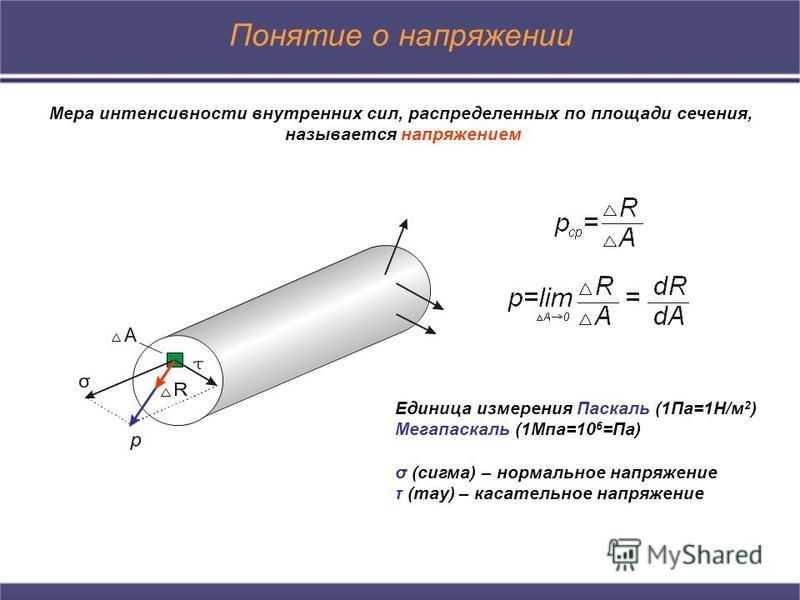
10
Основные гипотезы о деформируемом теле 1. Гипотеза о сплошности материала. Предполагается, что материал сплошь заполняет форму тела. 2. Гипотеза об однородности и изотропности. В любом объеме и в любом направлении свойства материала считаются одинаковыми. 3. Гипотеза о малости деформаций. Деформации малы по сравнению с размерами тела. 4. Гипотеза об идеальной упругости материала. Это означает, что сразу же после снятия нагрузки тело восстанавливает свои первоначальные размеры и форму. 5. Принцип независимости действия сил. Результат действия на тело системы внешних нагрузок равен сумме результатов от действия каждой из этих нагрузок в отдельности. 6. Гипотеза плоских сечений. Поперечные сечения, плоские и перпендикулярные оси тела до деформации, остаются плоскими и после деформации.

Особенности механики твердого тела
Твердое тело, которое систематически принимает разнообразные ориентации в любом пространстве, можно считать состоящим из огромного количества материальных точек. Это просто математический метод, помогающий расширить применимость теорий движения частиц, но не имеющий ничего общего с теорией атомного строения реального вещества. Поскольку материальные точки исследуемого тела будут направляться в разных направлениях с различными скоростями, приходится применять процедуру суммирования.
В этом случае, нетрудно определить кинетическую энергию цилиндра, если заранее известен вращающегося вокруг неподвижного вектора с угловой скоростью параметр. Момент инерции можно вычислить посредством интегрирования, и для однородного предмета равновесие всех сил возможно, если пластина не двигалась, следовательно, компоненты среды удовлетворяют условию векторной стабильности. В результате выполняется выведенное на изначальном этапе проектирования соотношение. Оба эти принципа составляют базу теории строительной механики и необходимы при возведении мостов и зданий.
Изложенное возможно обобщить на тот случай, когда отсутствуют неподвижные линии и физическое тело свободно вращается в любом пространстве. При таком процессе имеются три момента инерции, относящиеся к «ключевым осям». Проводившиеся постулаты в механике твердого вещества упрощаются, если пользоваться существующими обозначениями математического анализа, в которых предполагается предельный переход $(t → t0)$, так что нет надобности все время думать, как решить этот вопрос.
Интересно, что Ньютон первым применил принципы интегрального и дифференциального исчисления при решении сложных физических задач, а последующее становление механики как комплексной науки было делом таких выдающихся математиков, как Ж.Лагранж, Л.Эйлер, П.Лаплас и К.Якоби. Каждый из указанных исследователей находил в ньютоновском учении источник вдохновения для своих универсальных математических изысканий.
Почему sopromato.ru – лучший сайт о сопромате?
sopromato.ru не перегружен лишней информацией, содержит только важные сведения по сопромату, имеет удобную навигацию, содержит много справочной информации, полезной студентам технических ВУЗов:
- лекции по сопромату
- примеры решения задач по сопромату
- книги по сопромату
- сортамент фасонных профилей: уголок, швеллер, сортамент двутаврового профиля(используется в расчетах на прочность и жесткость)
- шпаргалки по сопромату
- вопросы к экзамену по сопромату
Кто ищет, тот всегда находит, а sopromato.ru поможет получить быстрый результат и оказать помощь тем, кто изучает сопромат
Таблица сравнения свойств материалов
| Свойство | Определение | Примеры материалов |
|---|---|---|
| Прочность | Способность материала сопротивляться разрушению под воздействием нагрузки | Сталь, бетон, дерево |
| Упругость | Способность материала возвращаться в исходное состояние после удаления нагрузки | Резина, сталь |
| Пластичность | Способность материала деформироваться без разрушения под воздействием нагрузки | Алюминий, медь, пластик |
| Твердость | Способность материала сопротивляться проникновению других твердых тел | Алмаз, стекло, керамика |
| Износостойкость | Способность материала сохранять свои свойства при трении и износе | Сталь, титан, карбид вольфрама |
Предисловие
Механика деформируемого твердого тела, как представляется автору, должна рассматриваться как единая наука, объединяющая те научные дисциплины, которые по традиции излагаются и изучаются раздельно. С другой стороны, это именно глава механики сплошной среды, т. е. феноменологическая теория, стремящаяся найти адекватное математическое описание совокупности опытных фактов, устанавливаемых макроэкспериментом. Для механика недостаточно написать определяющие уравнения, нужно уметь их решать при данных граничных условиях и решать возможно точно. Поэтому та картина, которую строит механик, может иногда показаться чрезмерно упрощенной. Но механик вынужден блуждать между Сциллой и Харибдой; с одной стороны, его уравнения должны достаточно точно отражать действительность, с другой — быть доступными для интегрирования.
Содержание предлагаемой читателю книги состоит из глав, материал которых практически весь излагался автором в лекциях на механико-математическом факультете МГУ и в других университетах. Она разбита на три части. Первая из них написана на вполне элементарном уровне. На примере простейших стержневых систем автор стремился изложить основные идеи общей теории упругих и пластических сред. Вторая часть посвящена теории упругости и ее приложениям. Наконец третья, последняя часть относится к проявлениям неупругости — теории пластичности, ползучести, механике разрушения.
Автор приносит глубокую благодарность В.В. Болотину и И.В. Гольденблатту, просмотревшим рукопись.































