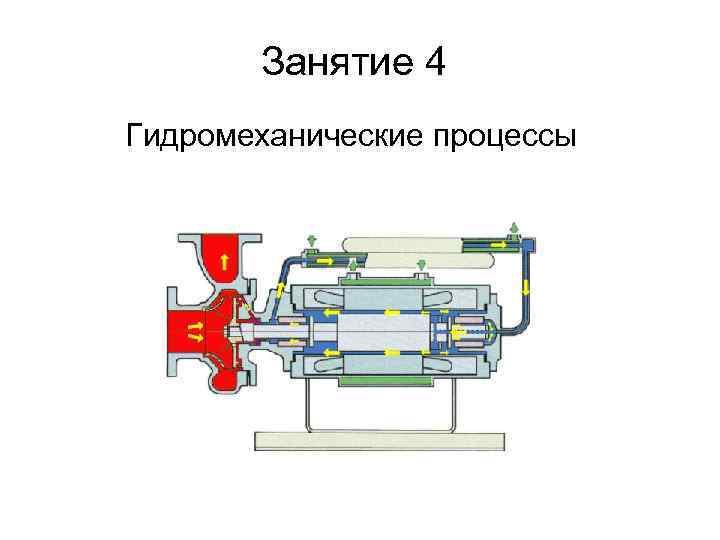
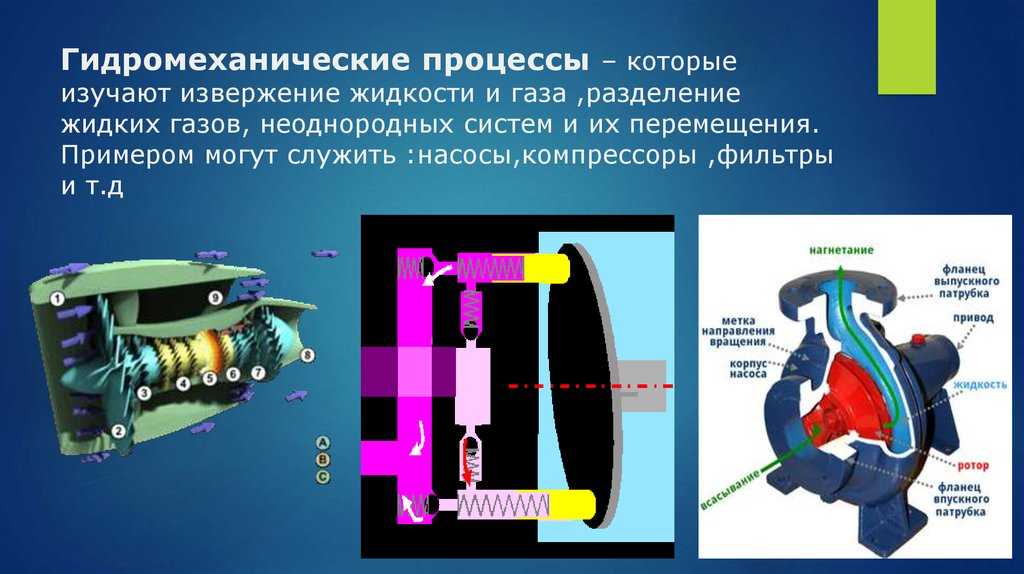
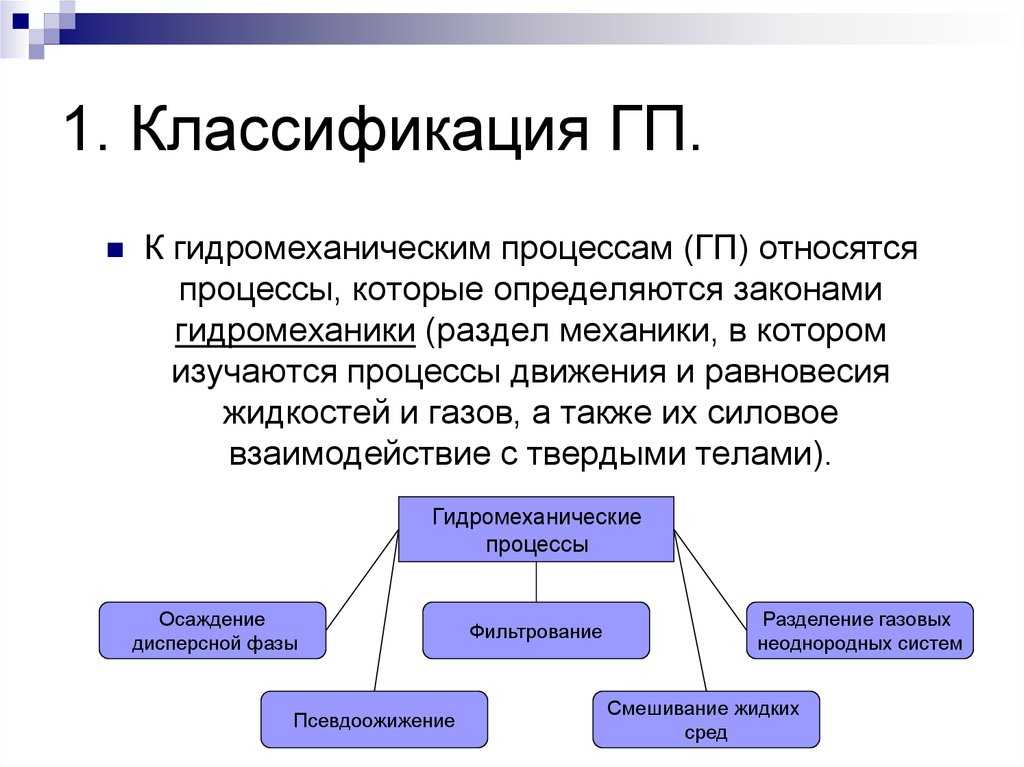
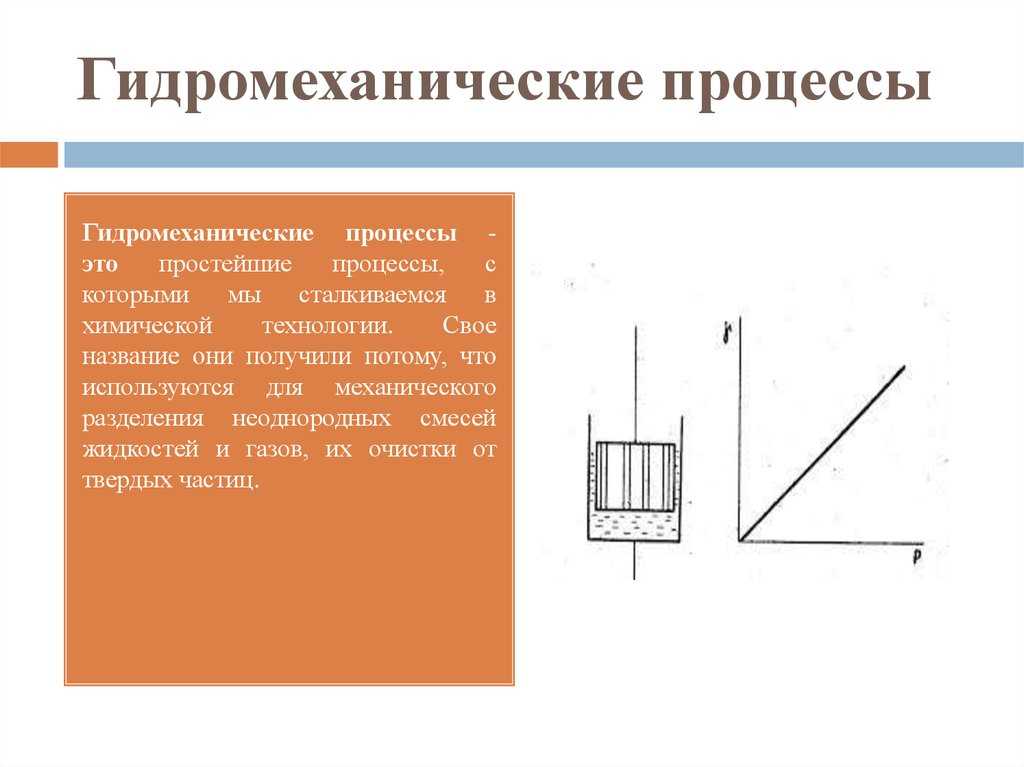
Поток жидкости и его параметры
Поток жидкости характеризуется такими параметрами как площадь живого сечения S, расход жидкости Q(G), средняя скорость движения v.
Живое сечение потока — это сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.
Векторы скорости частиц имеют некоторое расхождение в потоке жидкости.
Живым сечением потока жидкости называется сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.
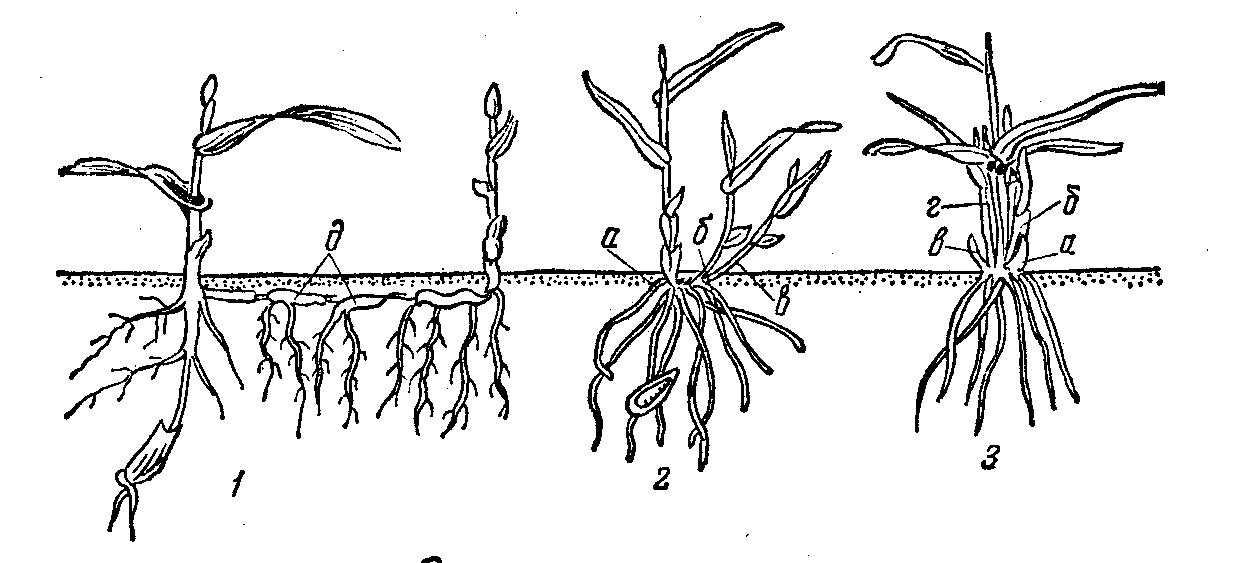
Поэтому живое сечение потока — криволинейная плоскость (рис. а, линия I—I) В виду незначительного расхождения векторов скорости в гидродинамике за живое сечение принимается плоскость, расположенная перпендикулярно скорости движения жидкости в средней точке потока.
Расход жидкости — это количество жидкости, протекающей через живое сечение потока в единицу времени. Расход может определяться в массовых долях G и объемных Q.
Средняя скорость движения жидкости — это средняя скорость частиц в живом сечении потока.
Если в живом сечении потока, движущегося, например, в трубе, построить векторы скорости частиц и соединить концы этих векторов, то получится график изменения скоростей (эпюра скоростей).
Если площадь такой эпюры разделить на диаметр данной трубы, то получится значение средней скорости движения жидкости в данном сечении:
Объемный расход жидкости рассчитывается по формуле:
Параметры потока жидкости определяют характер движения жидкости. При этом оно может быть установившимся и неустановившимся, равномерным и неравномерным, неразрывным и кавитационным, ламинарным и турбулентным.
Если параметры потока жидкости не изменяются во времени, то ее движение называется установившимся.
Равномерным называется движение, при котором параметры потока не изменяются по длине трубопровода или канала. Например, движение жидкости по трубе постоянного диаметра является равномерным.
Неразрывным называется движение жидкости, при котором она перемещается сплошным потоком, заполняющим весь объем трубопровода.
Отрыв потока от стенок трубопровода или от обтекаемого предмета приводит к возникновению кавитации.
Кавитацией называется образование в жидкости пустот, заполненных газом, паром или их смесью.
Кавитация возникает в результате местного уменьшения давления ниже критического значения pкр при данной температуре (для воды ркр= 101,3 кПа при Т= 373 К или ркр= 12,18 кПа при Т= 323 К и т. д.). При попадании таких пузырьков в зону, где давление выше критического, в эти пустоты устремляются частицы жидкости, что приводит к резкому возрастанию давления и температуры. Поэтому кавитация неблагоприятно отражается на работе гидротурбин, жидкостных насосов и других элементов гидравлических устройств.
Ламинарное движение — это упорядоченное движение жидкости без перемешивания между ее соседними слоями. При ламинарном течении скорость и силы инерции, как правило, невелики, а силы трения значительны. При увеличении скорости до некоторого порогового значения ламинарный режим течения переходит в турбулентный.
Турбулентное движение — это течение жидкости, при котором ее частицы совершают неустановившееся беспорядочное движение по сложным траекториям. При турбулентном течении скорость жидкости и ее давление в каждой точке потока хаотически изменяется, при этом происходит интенсивное перемешивание движущейся жидкости.
Для определения режима движения жидкости существуют условия, согласно которым скорость потока может быть больше или меньше той критической скорости, когда ламинарное движение переходит в турбулентное и наоборот.
Однако установлен и более универсальный критерий, который называют критерием или числом Рейнольдса:
Опытами было установлено, что в момент перехода ламинарного режима движения жидкости в турбулентный Re = 2320.
Число Рейнольдса, при котором ламинарный режим переходит в турбулентный, называется критическим. Следовательно, при Re 2320 — турбулентное. Отсюда критическая скорость для любой жидкости:
Поток жидкости через поверхность
Как и при изучении криволинейных интегралов, начнём с физической задачи. Пусть через объём $\mathbf > $ течёт поток жидкости, имеющий скорость $\bar (M)$ в точке $\mathbf > $. Пусть в $\mathbf > $ размещена проницаемая поверхность $\sigma $. Требуется найти количество $\Pi $ жидкости, протекающей через $\sigma $ за единицу времени. В дальнейшем мы будем называть это количество потоком через поверхность.
В случае, когда $\sigma $ — ограниченная плоская область и $\bar (M)= \overline $, решение очевидно. Это количество равно объёму, ограниченному цилиндрической поверхностью с основанием $\sigma $ и боковой стороной $\bar (M)$. Площадь основания объёма равна $\sigma $ , высота $h=\mbox _ > \bar =\vert \bar \vert \cos \varphi =\bar \cdot \bar $, т.е. равна скалярному произведению вектора скорости на единичный вектор нормали. Итак, $\Pi =\bar \bar \sigma $. Заметим, что изобразив на рисунке единичный вектор нормали, мы ввели на поверхности ориентацию. Так, применительно к рисунку справа, мы выбрали верхнюю сторону поверхности; если бы выбрали противоположную нормаль, поток изменил бы знак.
Возможны два способа представления этой величины.
- Обозначив $f=(\bar \cdot \bar )$, получим $\prod = f\cdot\sigma$
- Если в некоторой координатной системе $\bar (M)$ имеет координаты $\mathbf > $, $\mathbf > $, $\mathbf > $, единичный вектор $\bar (M)$ имеет координаты — направляющие косинусы $\cos \alpha ,\cos \beta ,\cos \gamma $, то $\Pi =\bar \bar \sigma =(P\cos \alpha +Q\cos \beta +R\cos \gamma )\sigma =P(\cos \alpha \cdot \sigma )+Q(\cos \beta \cdot \sigma )+R(\cos \gamma \cdot \sigma )$.
Чему равно произведение $\cos \gamma \cdot \sigma $? Произведение $\vert \cos \gamma \vert \cdot \sigma $ равно площади $s(D_ )$ проекции $D_ $ поверхности $\sigma $ на плоскость $\mathbf > $ .
Следовательно, $\cos \gamma \cdot \sigma $ равно $s(D_ )$, если $\cos \gamma \geqslant 0$ (M)$ на орт $\bar $ оси $\mathbf > $ положительна > . Этот случай соответствует верхнему рисунка.
Соответственно, $\cos \gamma \cdot \sigma $ равно $-s(D_ )$, если $\cos \gamma Огравление $\Rightarrow $
на ход технологических процессов
Протекание многих технологических
процессов зависит от поверхностной
энергии жидкостей. К таким процессам
относят процессы, предназначенные в той
или иной степени организовать структуру
строительного материала (приготовление
формовочных смесей, формование изделий,
создание газонаполненных пористых или
ячеистых структур и др.) или, наоборот,
разрушить ее (тонкое измельчение).
Изменяя величину поверхностного
натяжения жидкостей, можно управлять
этими процессами. Управление непосредственно
сказывается на ходе таких явлений,
как адсорбция, смачивание жидкостью
поверхности твердой фазы, формирование
избыточного давления в пленке жидкости
, покрывающей твердую частицу материала,
формирование пониженного давления в
тонких капиллярах, заполненных жидкостью,
формирование внутрипузырькового давления
в пенобетоне.
4.2.2 Дисперсные системы и неньютоновские жидкости
Дисперсными называют гетерогенные системы,
состоящие из двух (или более) фаз; обязательными
из которых являются дисперсная фаза
и дисперсионная среда.
Дисперсные системы являются
предметом изучения самостоятельной
науки – коллоидной химии.
В коллоидной химии понятие дисперсности
простирается на широкую область размеров:
от больших, чем простые молекулы, до видимых
невооруженным глазом частиц с размерами
от 10-9 до 10-4 м (от 1 нм до 100 мкм).
Дисперсность, то есть тонкая
раздробленность вещества, предопределяет
особые свойства дисперсных систем, обусловленные
значительной суммарной поверхностью
дисперсных частиц и, соответственно,
их высокой избыточной
поверхностной энергией.
Истинно коллоидными считают
частицы с размерами от 1 нм до
1 мкм – это высокодисперсные
системы. Но современная коллоидная
химия изучает и более грубодисперсные
системы с размерами частиц, превышающими
1 мкм, так как в таких системах в большей
или меньшей степени, но все же проявляются
коллоидные свойства.
Большинство строительных композиционных
материалов в своем исходном составе практически
в обязательном порядке содержат тонкодисперсную
составляющую (цемент, известь, гипс, измельченные
глина, песок и т.п.), что дает нам основание
относить их к дисперсным системам и распространять
на них законы коллоидной химии.
Это в свое время хорошо
показал во многих своих работах
академик П.А. Ребиндер, обосновавший самостоятельный
раздел науки – физикохимическую
механику дисперсных систем.
В зависимости от агрегатного
состояния и в соответствии с
классификацией коллоидной химии для
технологии строительных материалов характерны
следующие (таблица 3) типы дисперсных
систем.
Только по агрегатному
состоянию дисперсные системы, представленные
в таблице 3, можно разделить на жидкообразные
(в том числе и газообразные) и твердообразные
Мы сосредоточим свое внимание на первой
группе дисперсных систем, то есть на типах
1, 2, 3, 7. Выделенные системы мы вправе называть структурированными
жидкостями, так как между частицами
дисперсной фазы существуют силовые связи
Дисперсные системы по мере увеличения
концентрации дисперсной фазы и формирования
внутренних связей проходят обычно широкий
спектр состояний – от истинно жидких
(золи, суспензии) через структурированные
жидкости (различные формовочные смеси)
к твердообразным системам (цементный
камень, бетон).
Возникновение и развитие
пространственных структур, обладающих
фазовой устойчивостью, происходит
путем сцепления или срастания
частиц дисперсной фазы и приводит в системах
с жидкой средой к изменению характера
течения или к полному отверждению (переход
«золь→гель»). В зависимости от природы
действующих сил сцепления различают
(по Ребиндеру) два основных типа структур: коагуляционные
и конденсационные с фазовыми контактами.
Таблица 3 – Типы дисперсныхсистем
|
№ типа системы |
Дисперсная фаза |
Диспер-сионная среда |
Обозна-чение системы |
Тип системы по классификации коллоидной химии |
Технологические примеры |
|
Твердая |
Жидкая |
Т/Ж |
Золи, суспензии |
Разбавленные цементное, глиняное тесто; бетонная смесь; строительный раствор |
|
|
Жидкая |
Жидкая |
Ж/Ж |
Эмульсии |
Смазочный состав: эмульсия масла в воде |
|
|
Газообразная |
Жидкая |
Г/Ж |
Газовые жидкости, пены |
Пенобетонная смесь |
|
|
Твердая |
Твердая |
Т/Т |
Твердые коллоидные растворы |
Диабаз, базальт |
|
|
Жидкая |
Твердая |
Ж/Т |
Пористые капиллярные тела |
Отформованное бетонное изделие |
|
|
Газообразная |
Твердая |
Г/Т |
Пористые и капиллярные системы |
Ячеистый бетон |
|
|
Твердая |
Газообразная |
Г/Г |
Аэрозоли |
Цементновоздушная смесь при пневмотранспорте |
Коагуляционные
структуры образуются путем сцепления
частиц вандерваальсовыми силами в звенья,
цепочки, пространственные каркасы.
Структуры с фазовыми
контактами (конденсационные структуры)
образуются в результате срастания частиц
при спекании, гидратационном твердении
и т.п.
В гидродинамике наше внимание
будет сконцентрировано преимущественно
на структуре первого типа
значение
Гидромеханика – часть общей механики, в которой
изучается движение и равновесие жидкостей
и газов и механические воздействия жидкостей
и газов на находящиеся в них тела и ограничивающие
их стенки. Подразделяется на гидростатику
и гидродинамику.
Гидростатика рассматривает равновесие жидкостей
и газов в состоянии покоя, а также их воздействие
на находящиеся в них тела и ограждающие
стенки.
Гидродинамика – наука о движении несжимаемых
жидкостей и газов и воздействии жидкостей
и газов на обтекаемые ими твердые тела.
На специальности «Строительство»
основные положения гидродинамики изучаются
в дисциплине общепрофессионального цикла,
которая называется «Гидравлика». Однако
объем и содержание этой дисциплины совершенно
недостаточны для того, чтобы раскрыть
гидромеханическую сущность большинства
технологических процессов, в которых
гидромеханическая составляющая зачастую
играет определяющую роль.
Речь идет о таких процессах,
как перемешивание жидких и жидкообразных
масс с приготовлением формовочных и других
технологических смесей; фильтрация газов
через слои кусковых и зернистых материалов
при их обжиге; фильтрация жидкостей и
газов в процессах очистки; осаждение
и устойчивость твердых частиц в технологических
суспензиях, шламах, шликерах, растворных
и бетонных смесях; устойчивость или всплытие
пузырьков газа в технологии ячеистого
бетона; транспортирование по трубам в
газовой или жидкой среде зернистых и
кусковых материалов; формование бетонных
изделий и конструкций; создание требуемой
гидродинамической обстановки в печах
и сушилах и др. Это задачи о движении тел
в жидкостях, об образовании и движении
газовых пузырьков, о движении жидкостей
через неподвижные и пористые слои, о псевдоожиженном
состоянии порошковых и зернистых материалов,
о движении двухфазных потоков, о процессах
перемешивания и виброуплотнения.
Сложность гидромеханических
процессов строительных технологий
заключается и в том, что многие
технологические жидкости и жидкообразные
массы по своим реологическим свойствам
существенно отличаются от так называемых
ньютоновских (вязких) жидкостей, на которые
ориентирована классическая гидравлика.
Технологические жидкости и жидкообразные
массы по сравнению с неньютоновскими
жидкостями обладают рядом специфических
свойств таких, как пластичность, изменяющаяся
в процессе течения вязкость. Совершенно
не вписываются в классическое определение
«гидродинамики» такие моменты, как сжимаемость
жидкости (ячеистобетонные смеси), отсутствие
сплошности потока. Практическая технология
рассматривает задачи гидромеханики,
как правило, не в чистом виде, а в сочетании
с другими процессами, прежде всего –
тепловыми и массообменными, которые,
создавая температурную, барометрическую,
концентрационную неравновесность, существенно
влияют на ход гидродинамических процессов.
Это приходится учитывать в расчетах,
например, тепловых аппаратов.
4.2.1 Общие понятия
В гидромеханике термин «жидкость»
носит универсальный характер. Его
применяют к истинным жидкостям,
которые могут также называться
капельными, несжимаемыми, и к газам
и парам (сжимаемые жидкости). В
технологии строительных материалов и
изделий капельные жидкости бывают
представлены чистой водой, например,
для затворения бетонных и растворных
смесей; водными растворами различных
солей и полимерных веществ (ускорители
твердения бетона, пластификаторы, противоморозные
добавки и т.п.); маслами и им подобными
веществами (смазочные, пропиточные составы
и т.п.), другими истинными жидкостями.
Сжимаемые жидкости наиболее
часто бывают представлены атмосферным
воздухом (компрессорные установки, пневмоприводы
к технологическому оборудованию, воздуходутье
к печам и сушилам, пневмотранспорт); водяным
паром для тепловой обработки бетонных
и железобетонных изделий; природным горючим
газом как источником тепловой энергии
к обжиговым печам, сушильным установкам;
дымовыми газами, получаемыми при сгорании
топлива.
Именно на представленные
выше вещества распространяются теоретические
и практические положения классической
гидромеханики.
Однако строительная технология
не ограничивается только этими, так
называемыми ньютоновскими жидкостями.
Большинство наиболее сложных технологических
процессов связано с неньютоновскими
жидкостями в виде, например, шламов, шликеров,
глиняного и цементного теста, бетонов,
растворов, цементно-воздушных смесей
и т.п. Их течение происходит намного сложнее
того, чему посвящена классическая гидродинамика.
Поэтому прежде, чем приступит к изучению
процессов течения таких жидкостей, необходимо
проанализировать их состав, структуру,
реологические свойства, определить научные
подходы к изучению столь сложных систем.
4.2.3.1 Сущность поверхностного натяжения
Поверхностное натяжение
можно рассматривать как явление
нескомпенсированности межмолекулярных
сил (сил Ван-дер-Ваальса) на границе жидкой
фазы с несмачивающейся жидкостью, газом,
паром, стенкой сосуда. Наглядным примером
действия поверхностного натяжения является
шарообразная форма капель многих жидкостей
как следствие стремления этих жидкостей
понизить уровень поверхностной избыточной
энергии (в данном случае за счет сокращения
площади поверхности, которая для капли
оказывается самой малой по сравнению
с другими геометрическими формами при
фиксированной массе жидкости).
При диспергировании жидкости
(а равно – и других веществ)
образуется дополнительная поверхность
и, соответственно, избыточная энергия.
Исходя из этого поверхностное натяжение
(δ) можно представить как работу (А), затрачиваемую
на образование единицы новой поверхности
(S):
(15)
Из (15) вытекает следующая размерность поверхностного натяжения (в системе СИ): = [Дж/м2]. Поверхностное натяжение, представленное в виде (6.1), называют свободной поверхностной энергией.