Решение дифференциального уравнения колебаний
Решением дифференциального уравнения затухающих колебаний (3) является соотношение вида:
Уравнение (4) называется уравнением затухающих колебаний. В уравнении (4) видно, что амплитуда затухающих колебаний зависит от времени. Константы A и определяются начальными условиями. Амплитуда колебаний убывает и они в целом выглядят так, как представлено на рис. 1
рис. 1.
Период затухающих колебаний вычисляется по формуле (5):
Физический коэффициента затухания смысл состоит в том, что коэффициент затухания – величина, обратная времени релаксации. А время релаксации – это время, за которое амплитуда уменьшается в e раз. Однако коэффициент затухания не вполне характеризует затухание. Обычно затухание колебаний характеризуется декрементом затухания. Последний показывает, во сколько раз уменьшается амплитуда колебаний за время, равное периоду колебаний. То есть декремент затухания определяется так:
Логарифм декремента затухания называется логарифмическим декрементом, он, очевидно, равен:
Если колебательная система подвергается воздействию внешней периодической силы, то возникают так называемые вынужденные колебания, имеющие незатухающий характер.
Вынужденные колебания следует отличать от автоколебаний. В случае автоколебаний в системе предполагается специальный механизм, который в такт с собственными колебаниями «поставляет» в систему небольшие порции энергии.
Сложение гармонических колебаний
Рассмотрим
два случая такого сложения.
a)
Осциллятор участвует в двух
взаимно-перпендикулярных
колебаниях.
В
этом случае вдоль осей x и y действуют
две квазиупругие силы. Тогда
Для
того, чтобы найти траекторию осциллятора,
следует исключить из этих уравнений
время t.
Проще
всего это сделать в случае кратных
частот
:
Где n и m — целые числа.
В
этом случае траекторией осциллятора
будет некоторая замкнутая
кривая, называемая фигурой
Лиссажу
.
Пример
:
частоты колебаний по x и y одинаковы
( 1 = 2 =),
а разность фаз колебаний
(для простоты положим 1 =0).
.
Отсюда
находим:
—
фигурой Лиссажу будет эллипс.
б)
Осциллятор совершает колебания одного
направления
.
Пусть
таких колебаний пока будет два; тогда
где
и
—
фазы колебаний.
Аналитически
колебания складывать очень неудобно,
особенно, когда их
не
два, а несколько; поэтому обычно
используется геометрический метод
векторных диаграмм
.
Гармонический осциллятор
Колебаниями
вообще называются движения, повторяющиеся
во времени.
Если
эти повторения следуют через равные
промежутки времени, т.е. x(t+T)=x(t), то
колебания называются периодическими
.
Система, совершающая
колебания,
называется осциллятором
.
Колебания, которые совершает система,
предоставленная самой себе, называются
собственными, а частота колебаний в
этом случае — собственной
частотой
.
Гармоническими
колебаниями
называются колебания, происходящие по
закону sin или cos. Например,
x(t)=A
cos(t+ 0),
где
x(t) — смещение частицы от положения
равновесия, A — максимальное
смещение
или амплитуда
,
t+ 0
— фаза
колебаний, 0
—
начальная фаза (при t=0),
— циклическая
частота
,
— просто частота колебаний.
Система,
совершающая гармонические колебания,
называется гармоническим осциллятором.
Существенно, что амплитуда и частота
гармонических колебаний постоянны и
не зависят друг от друга.
Условия
возникновения гармонических колебаний
:на
частицу (или систему частиц) должна
действовать сила или момент сил,
пропорциональные смещению частицы из
положения равновесия и
стремящиеся
вернуть ее в положение равновесия. Такая
сила (или момент сил)
называется
квазиупругой
;
она имеет вид
,
где k называется квазижесткостью.
В
частности это может быть и просто упругая
сила, приводящая в колебания пружинный
маятник, колеблющийся вдоль оси x.
Уравнение движения такого маятника
имеет вид:
или
,
где
введено обозначение
.
Непосредственной
подстановкой нетрудно убедиться, что
решением уравнения
является
функция
x=A
cos( 0 t+ 0),
где
A и 0
—
постоянные величины
,
для определения которых следует задать
два начальных
условия
:
положение x(0)=x 0
частицы и ее скорость v х (0)=v 0
в начальный (нулевой) момент времени.
Это
уравнение представляет собою динамическое
уравнение любых
гармонических
колебаний с собственной частотой 0 .
Для грузика на
пружинке
период колебаний пружинного маятника
.
Условия существования колебаний
Колебательные процессы широко распространены в окружающем нас мире.
Рис. 1. Колебания в природе и технике.
Независимо от природы рассматриваемых явлений и систем, колебания в этих системах могут возникать при выполнении следующих условий.
- В системе должно существовать некоторое единственное положение равновесия;
- Система должна быть выведена из равновесия;
- Должна существовать сила, которая стремится вернуть систему в положение равновесия;
- Потери энергии в системе либо должны быть невелики, либо должны постоянно восполняться из внешних источников.
Из анализа данных условий можно составить уравнение, описывающее процессы, проходящие в системе.
Если сила стремится вернуть систему в положение равновесия, значит, эта сила пропорциональна (через коэффициент пропорциональности $k$) отклонению системы от этого положения. Направлена она против отклонения, значит, имеет противоположный знак. То есть, для механического случая:
$$F=-kx$$
Из механики известно, что ускорение движения материальной точки пропорционально силе, воздействующей на материальную точку. Следовательно:
$$a=-kx$$
Ускорение – это производная скорости. А скорость – производная расстояния. То есть, вторая производная расстояния должна быть пропорциональна самому расстоянию, взятому со знаком «минус».
$$x”=-kx$$
Это дифференциальное уравнение, описывающее колебательный процесс.
Физический и математический маятники
Физический
маятник
— это любое физическое тело, совершающее
колебания
вокруг оси, не проходящей через центр
масс, в поле сил тяжести.
Для
того, чтобы
собственные колебания системы были
гармоническим, необходимо, чтобы
амплитуда этих колебаний была мала
.
Кстати, то же справедливо и для пружинки:
F упр =-kx
только для малых деформаций пружинки
x.
Период
колебаний определяется формулой:
.
Заметим,
что квазиупругим здесь является момент
силы тяжести
M я
=
— mgd ,
пропорциональный угловому отклонению
.
Частным
случаем физического маятника является
математический
маятник
—
точечная масса, подвешенная на невесомой
нерастяжимой нити длины l. Период малых
колебаний
математического маятника
Плоское движение
Движение
твердого тела, при котором центр масс
перемещается в фиксированной плоскости,
а ось его вращения, проходящая через
центр масс, остается перпендикулярной
к этой плоскости, называется плоским
движением
.
Это движение можно свести к совокупности
поступательного движения и вращения
вокруг неподвижной
(закрепленной) оси
,
так как в Ц-системе ось вращения,
действительно, остается неподвижной.
Поэтому плоское движение описывается
упрощенной системой двух уравнений
движения:
Кинетическая
энергия тела, совершающего плоское
движение, будет:
и
окончательно
,
так
как в данном случае i »
— скорость вращения i-ой точки вокруг
неподвижной оси.
Колебания
Момент инерции и его вычисление
Согласно
определению, момент
инерции тела относительно оси равен
сумме произведений масс частиц на
квадраты их расстояний до оси вращения
или
Однако,
эта формула непригодна для вычисления
момента инерции; так как масса твердого
тела распределена непрерывно, то сумму
следует заменить на интеграл. Поэтому
для вычисления момента инерции тело
разбивают на бесконечно малые объемы
dV с массой dm=dV.
Тогда
где
R — расстояние элемента dV от оси вращения.
Если
момент инерции I C
относительно оси, проходящей через
центр масс, известен, то можно легко
вычислить момент инерции относительно
любой параллельной оси О, проходящей
на расстоянии d от центра масс или
I O =I C +md 2 ,
Это
соотношение называется теоремой
Штейнера
:
момент инерции тела относительно
произвольной оси равен сумме момента
инерции относительно оси параллельной
ей и проходящей через центр масс и
произведения массы тела на квадрат
расстояния между осями.
Виды колебаний
Свободные
колебания совершаются
под действием внутренних сил системы
после того, как система была выведена
из положения равновесия. Чтобы свободные
колебания были гармоническими,
необходимо, чтобы колебательная система
была линейной (описывалась линейными
уравнениями движения), и в ней отсутствовала
диссипация энергии (последняя вызвала
бы затухание).
Вынужденные
колебания совершаются
под воздействием внешней периодической
силы. Чтобы они были гармоническими,
достаточно чтобы колебательная система
была линейной (описывалась линейными
уравнениями движения), а внешняя сила
сама менялась со временем как гармоническое
колебание (то есть чтобы зависимость
от времени этой силы была синусоидальной).
Уравнение колебаний
Полученное дифференциальное уравнение решается в высшей математике. Его единственным решением является круговая функция (синус или косинус).
$$x(t)=A sin(\sqrt kt+\varphi)$$
Проверим, так ли это ?
Для нахождения скорости надо взять производную. Получим:
$$v(t)=A\sqrt k cos(\sqrt kt+\varphi)$$
А если взять вторую производную, получим ускорение:
$$a(t)=-Ak sin(\sqrt kt+\varphi) = -kx(t)$$
В итоге мы видим, что формула ускорения оказалось равной первоначальной функции расстояния, взятой с противоположным знаком, и умноженным на коэффициент $k$. То есть, можно сделать вывод, что исходное дифференциальное уравнение решено правильно.
Вынужденные колебания
Вынужденные
колебания
возникают при действии на осциллятор
внешней
периодической силы, изменяющейся по
гармоническому закону
с
частотой вн:
.
Динамическое
уравнение вынужденных колебаний:
Для
установившегося
режима колебаний
решением
уравнения будет гармоническая функция:
где
A — амплитуда вынужденных колебаний, а
— отставание по фазе
от
вынуждающей силы.
Амплитуда
установившихся вынужденных колебаний:
Отставание
по фазе установившихся вынужденных
колебаний от внешней
вынуждающей
силы:
.
\hs
Итак: установившиеся вынужденные
колебания происходят
с
постоянной, не зависящей от времени
амплитудой, т.е. не затухают,
несмотря
на сопротивление среды. Это объясняется
тем, что работа
внешней
силы идет на
увеличение
механической энергии осциллятора и
полностью компенсирует
ее
убывание, происходящее из-за действия
диссипативной силы сопротивления
Затухающие гармонические колебания
В
реальной ситуации на осциллятор со
стороны окружающей среды всегда действуют
диссипативные силы (вязкого трения,
сопротивления среды)
,
которые замедляют движение. Уравнение
движения тогда принимает вид:
.
Обозначая
и
,
получаем динамическое уравнение
собственных затухающих гармонических
колебаний:
.
Как
и в случае незатухающих колебаний, это
общая форма уравнения.
При
не слишком большом сопротивлении среды
Функция
представляет
собою убывающую по экспоненте амплитуду
колебаний. Это уменьшение амплитуды
называется релаксацией
(ослаблением) колебаний, а
называется коэффициентом
затухания
колебаний.
Время
,
за которое амплитуда колебаний уменьшается
в e=2,71828 раз,
называется
временем
релаксации
.
Кроме
коэффициента затухания, вводится еще
одна характеристика,
называемая
логарифмическим
декрементом затухания
— это натуральный
логарифм
отношения амплитуд (или смещений) через
период:
Частота
собственных затухающих колебаний
зависит
не только от величины квазиупругой силы
и массы тела, но и от
сопротивления
среды.
2.2. RLC-контур. Свободные колебания window.top.document.title = «2.2. RLC-контур. Свободные колебания»;
В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рис. 2.2.1).
| Рисунок 2.2.1.Последовательный RLC-контур |
Когда ключ K находится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер.
Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде
qqtRLC
Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда
Здесь принято обозначение: Уравнение (*) описывает свободные колебания в LC-контуре в отсутствие затухания. По виду оно в точности совпадает с уравнением свободных колебаний груза на пружине в отсутствие сил трения (ч. I, § 2.2). Рис. 2.2.2 иллюстрирует аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q (t) конденсатора и смещения x (t) груза от положения равновесия, а также графики тока J (t) и скорости груза υ (t) за один период колебаний.
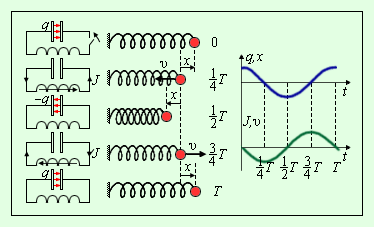 |
| Рисунок 2.2.2.Аналогия процессов свободных электрических и механических колебаний |
Сравнение свободных колебаний груза на пружине и процессов в электрическом колебательном контуре позволяет сделать заключение об аналогии между электрическими и механическими величинами. Эти аналогии представлены в таблице 1.
|
||||||||||||||||||||||||||||||||||
| Таблица 1 |
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону
Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний
Амплитуда q и начальная фаза φ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для процесса колебаний, который начнется в контуре (рис. 2.2.1) после переключения ключа K в положение 2, q = C, φ = 0.
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 2.2.3).
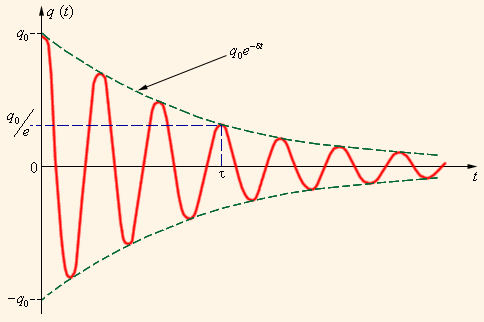 |
| Рисунок 2.2.3.Затухающие колебания в контуре |
Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: Fтр = – βυ. Коэффициент β в этой формуле аналогичен сопротивлению R электрического контура. Уравнение свободных колебаний в контуре при наличии затухания имеет вид
Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция
exp (–δt)Re ≈ 2,7 разавременем затухания
NQ
Для RLC-контура добротность Q выражается формулой
Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.
Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω идеального контура с теми же значениями L и C. Но при Q ≥ (5÷10) этим различием можно пренебречь.
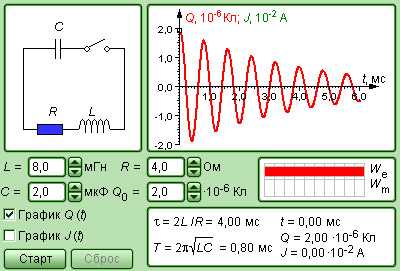 |
|
Модель. Свободные колебания в RLC-контуре |
Уравнение гармонических колебаний
|
Уравнение
|
дает зависимость
колеблющейся величины S от
времени t;
это и есть уравнение свободных
гармонических колебаний в явном виде.
Однако обычно под уравнением колебаний
понимают иную запись этого уравнения,
в дифференциальной форме. Возьмем для
определенности уравнение (1) в виде
дважды
продифференцируем его по времени:
Видно,
что выполняется следующее соотношение:
которое и называется
уравнением свободных гармонических
колебаний (в дифференциальной форме).
Уравнение (1) является решением
дифференциального уравнения (2). Поскольку
уравнение (2) — дифференциальное уравнение
второго порядка, необходимы два начальных
условия для получения полного решения
(то есть определения входящих в уравнение
(1) констант A и );
например, положение и скорость
колебательной системы при t =
0.
Математи́ческий
ма́ятник — осциллятор,
представляющий собой механическую
систему,
состоящую изматериальной
точки,
находящейся на невесомой нерастяжимой нити
или на невесомом стержне в
однородном поле сил тяготения. Период малых
собственных колебаний математического
маятника длины l неподвижно
подвешенного в однородном поле тяжести
с ускорением
свободного падения g равен
и не
зависит от амплитуды и массы маятника.
Физический
маятник — осциллятор,
представляющий собой твёрдое
тело,
совершающее колебания в поле каких-либо сил относительно
точки, не являющейся центром
масс этого
тела, или неподвижной оси, перпендикулярной
направлению действия сил и не проходящей
через центр масс этого тела.
Примеры решения задач
ПРИМЕР 1
| Задание | Найдите энергию свободных колебаний груза подвешенного на пружине Рассмотрите случай физического маятника, зная, что жесткость пружины k, амплитуда колебаний A.
рис. 1.1 |
| Решение |
Найдем энергию свободных колебаний. Она представлена двумя видами энергии: кинетической и потенциальной. Для шарика, подвешенного на пружине: Колебания шарика описывает уравнение колебаний: запишем уравнение колебаний скорости шарика, зная, что , движение происходит только вдоль оси Х следовательно: Подставим (1.2) и (1.3) в (1.1), получим: зная, что для физического маятника |
| Ответ | Энергия свободных колебаний пропорциональна квадрату амплитуды колебаний |























![Глава 21 гармонический осциллятор. 2a. пространство. время. движение [calibre 0.8.45]](http://site-edu.ru/wp-content/uploads/6/f/a/6faba432ee4a1f7f974c8d64749754ea.jpeg)






