Теоретическая механика статика кинематика динамика. статика

Основные признаки классификации

При классификации нагрузок в сопротивлении материалов используются основные признаки, которые позволяют выделить различные виды нагрузок и определить их характеристики

Важно помнить, что нагрузки могут действовать как отдельно, так и в сочетании друг с другом, что влияет на общую классификацию

Основные признаки классификации нагрузок включают:

1. Вид нагрузки: нагрузки могут быть статическими, динамическими или комбинированными. Статические нагрузки действуют равномерно и не изменяют своего направления и величины со временем. Динамические нагрузки изменяют свои параметры во времени – например, постепенно возрастая или уменьшаясь. Комбинированные нагрузки представляют собой комбинацию статических и динамических воздействий.

2. Способ приложения нагрузки: нагрузки могут быть приложены к материалу с помощью различных способов, например, точечного, линейного или поверхностного приложения нагрузки.

3. Механизм воздействия нагрузки: нагрузки могут быть распределенными или концентрированными. Распределенные нагрузки равномерно распределены по области воздействия, в то время как концентрированные нагрузки сосредоточены в определенной точке.

4. Направление нагрузки: нагрузки могут действовать в разных направлениях. Например, нагрузка может быть направленной в одну сторону, двусторонней (в обе стороны) или изменяющей свое направление с течением времени.

5. Временная характеристика: нагрузки могут быть постоянными, временными или переменными. Постоянные нагрузки остаются постоянными во времени, временные нагрузки воздействуют на материал на определенный период времени, а переменные нагрузки изменяют свои параметры с течением времени.

6. Сила нагрузки: нагрузки могут оказывать давление или тяготеть на материал. Сила нагрузки может быть постоянной или изменяться в зависимости от условий воздействия.

Учитывая эти основные признаки классификации, можно провести более точную оценку и анализ нагрузок в сопротивлении материалов, что позволяет разработать более эффективные конструкции и механизмы.

Примеры решения задач

Решение примеров по теме: «Статика твердого тела»

Пример 1. Условия равновесия

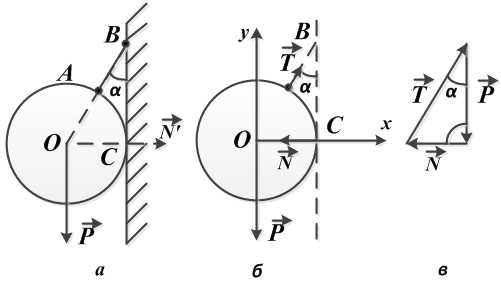
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.

Дано: P = 10 Н; α = 45°Найти: N, T — ?

Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.

Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).

Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).

При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).

В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:

После подстановки в формулы числовых значений, получим:.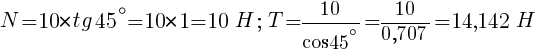

Ответ: .

Решение примеров по теме: «Кинематика»

Пример 2. Уравнение траектории точки

Дано:
Движение точки задано уравнениями ;
(x, у — в сантиметрах, t — в секундах).Найти: уравнение траектории точки в координатной форме.

Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:.

Опуская промежуточные выражения, получаем уравнение траектории:.

Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).

Ответ: .

Решение примеров по теме: «Динамика»

Пример 3. Основной закон динамики точки

Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.

Дано: m = 10 кг; a = 0,5 м/с2.Найти: F — ?

Решение.
Согласно основному закону динамики: .

Подставив значения в формулу, получим:

Ответ: сила, сообщающая массе, равной 10 кг,
ускорение 0,5 м/с2, равна 5 Н.

В помощь студенту

• Формулы, правила, законы, теоремы, уравнения, примеры решения задач
• Теоретические основы электротехники
• Электрические машины
• Высшая математика

Основные принципы классификации нагрузок

Основные принципы классификации нагрузок включают следующие аспекты:

1. Статические нагрузки: это нагрузки, которые оказывают постоянное воздействие на материал. Они могут быть постоянными или изменяться со временем, но не вызывают заметных изменений в структуре материала. Примерами статических нагрузок являются собственный вес конструкции или постоянное давление на определенную точку материала.
2. Динамические нагрузки: это нагрузки, вызываемые движением или вибрацией. Они могут быть быстрыми или медленными, но вызывают временные изменения в структуре материала. Примерами динамических нагрузок являются удары, вибрации и перегрузки при работе машин и оборудования.
3. Силовые нагрузки: это нагрузки, вызываемые применением силы на материал. Они могут быть как постоянными, так и изменяющимися со временем. Примерами силовых нагрузок являются сжатие, растяжение, изгиб и кручение материала.
4. Комбинированные нагрузки: это нагрузки, которые сочетают в себе несколько типов нагрузок одновременно. Комбинированные нагрузки могут быть особенно опасными, так как их воздействие на материал может быть неоднородным и вызывать различные виды повреждений. Примерами комбинированных нагрузок являются силовые нагрузки, сопровождающиеся вибрациями или быстрыми изменениями внешних условий.

Правильная классификация нагрузок позволяет инженерам и проектировщикам более точно оценить потенциальные риски и выбрать наиболее эффективные методы усиления и защиты материалов. Она также позволяет оптимизировать конструкцию и улучшить ее безопасность и надежность.

Металлические конструкции. Часть I — Классификация нагрузок и их сочетаний

Содержание материала

• Металлические конструкции. Часть I

• История металлоконструкций (2)

• История металлоконструкций (3)

• История металлоконструкций (4)

• РАЗДЕЛ 1. Элементы металлоконструкций. Номенклатура и область применения

• Номенклатура и область применения металлоконструкций (2)

• Свойства и работа строительных сталей и алюминиевых сплавов

• Классификация сталей

• Выбор сталей для строительных конструкций

• Влияние различных факторов на свойства стали

• Виды разрушений

• Работа металла под нагрузкой

• Работа металла под нагрузкой (2)

• РАЗДЕЛ 2. Основы расчета металлических конструкций. Основные понятия

• Основные положения расчета металлических конструкций

• Классификация нагрузок и их сочетаний

• Напряженное и деформированное состояние центрально нагруженных элементов

• Напряженное и деформированное состояние центрально нагруженных элементов (2)

• Основы расчета изгибаемых элементов

• Основы расчета изгибаемых элементов (2)

• Основы расчета центрально сжатых стержней

• Основы расчета центрально сжатых стержней (2)

• Основы расчета на прочность, устойчивость, усталость

• Основы расчета на прочность, устойчивость, усталость (2)

• РАЗДЕЛ 3. Сортамент. Характеристика основных профилей

• Листовая сталь

• Уголковые профили, швеллеры, двутавры

• Различные профили

• Профили из алюминиевых сплавов. Правила использования профилей

• РАЗДЕЛ 4. Сварные соединения. Виды сварки

• Виды сварных швов и соединений

• Виды сварных швов и соединений (2)

• Дефекты сварных соединений

• Дефекты сварных соединений (2)

• Конструирование и работа сварных соединений

• Расчет сварных соединений

• Расчет сварных соединений (2)

• Расчет сварных соединений (3)

• Расчет сварных соединений (4)

• Все страницы

Страница 16 из 39

2.3.Классификация нагрузок и их сочетаний

При методике предельных состояний все нагрузки классифицированы в зависимости от вероятности их воздействия на нормативные и расчетные.

По признаку воздействия нагрузки разделяются на постоянные и временные. Последние могут быть длительного и кратковременного воздействия.

Кроме того, есть нагрузки, которые выделяются в разряд особых нагрузок и воздействий.

Постоянные нагрузки – собственный вес несущих и ограждающих конструкций, давление грунта, предварительное напряжение.

Временные длительные нагрузки – вес стационарного технологического оборудования, вес складируемых материалов в хранилищах, давление газов, жидкостей и сыпучих материалов в емкостях и т.д.

Кратковременные нагрузки – нормативные нагрузки от снега, ветра, подвижного подъемно-транспортного оборудования, массы людей, животных и т.п.

Особые нагрузки – сейсмические воздействия, взрывные воздействия. Нагрузки, возникающие в процессе монтажа конструкций. Нагрузки, связанные с поломкой технологического оборудования, воздействия, связанные с деформациями основания в связи с изменениями структуры грунта (просадочные грунты, осадка грунтов в карстовых районах и над подземными выработками).

Существует иногда термин “полезная нагрузка”. Полезной называют нагрузки, восприятие которых составляет цельное назначение сооружений, например, вес людей для пешеходного моста. Они бывают как временными, так и постоянным, например, вес монументального выставочного сооружения является постоянной нагрузкой для постамента. Для фундамента вес всех вышележащих конструкций также представляет полезную нагрузку.

При действии на конструкцию нескольких видов нагрузок усилия в ней определяются как при самых неблагоприятных сочетаниях с использованием коэффициентов сочетаний .

В СНиПе 2.01.07-85 “ Нагрузки и воздействия” различают:

основные сочетания, состоящие из постоянных и временных нагрузок;

особые сочетания, состоящие из постоянных, временных и одной из особых нагрузок.

При основном сочетании, включающем одну временную нагрузку, коэффициент сочетаний . При большем числе временных нагрузок, последние умножаются на коэффициент сочетаний .

В особых сочетаниях временные нагрузки учитываются с коэффициентом сочетаний , а особая нагрузка — с коэффициентом . Во всех видах сочетаний постоянная нагрузка имеет коэффициент .

Основные направления, формулы и пояснения

В механике выделяют следующие основные разделы:

• кинематику (науку, которая описывает количественные характеристики движения: время, расстояние, скорость);
• статику (науку о телах, находящихся в равновесии при воздействии на них внешних сил);
• динамику (науку о движении тел при воздействии на них внешних сил).

Механика изучает движения материальных тел, при этом все материальные объекты делятся на 3 вида:

1. Материальная точка (это материальное тело, чьи размеры можно не учитывать). 
2. Твердое тело (тело, в котором расстояние между любыми его точками неизменно).
3. Сплошная среда (газ, жидкость и другие вещества, подверженные деформации).

По предмету изучения механику подразделяют на:

• теоретическую (наука об общих законах движения, которая изучает и описывает движение материальных точек и твердых тел);
• механику сплошных сред (наука, которая изучает движение тел, непрерывно заполняющих пространство и представляющих собой сплошную среду);
• прикладную (наука, которая описывает принцип работы технических механизмов).

Рассмотрим детальнее основные разделы механики. И начнем с кинематики.

Уравнения Лагранжа

Обобщенные координаты q 1
, q 2
, …, q n

— это совокупность n
величин, которые однозначно определяют положение системы.

Число обобщенных координат n
совпадает с числом степеней свободы системы.

Обобщенные скорости
— это производные от обобщенных координат по времени t
.

Обобщенные силы Q 1
, Q 2
, …, Q n

. Рассмотрим возможное перемещение системы, при котором координата q k
получит перемещение δq k
.
Остальные координаты остаются неизменными. Пусть δA k
— это работа, совершаемая внешними силами при таком перемещении. ТогдаδA k = Q k δq k
,
или .

Если, при возможном перемещении системы, изменяются все координаты, то работа, совершаемая внешними силами при таком перемещении, имеет вид:δA = Q 1
δq 1
+ Q 2
δq 2
+ … + Q n δq n
.
Тогда обобщенные силы являются частными производными от работы по перемещениям: .

Для потенциальных сил
с потенциалом Π
,
.

Уравнения Лагранжа
— это уравнения движения механической системы в обобщенных координатах:

Здесь T
— кинетическая энергия. Она является функцией от обобщенных координат, скоростей и, возможно, времени. Поэтому ее частная производная также является функцией от обобщенных координат, скоростей и времени. Далее нужно учесть, что координаты и скорости являются функциями от времени. Поэтому для нахождения полной производной по времени нужно применить правило дифференцирования сложной функции: .

Использованная литература: С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

В курсе рассматриваются: кинематика точки и твёрдого тела (причём с разных точек зрения предлагается рассмотреть проблему ориентации твердого тела), классические задачи динамики механических систем и динамики твердого тела, элементы небесной механики, движение систем переменного состава, теория удара, дифференциальные уравнения аналитической динамики.

В курсе представлены все традиционные разделы теоретической механики, однако особое внимание уделено рассмотрению наиболее содержательных и ценных для теории и приложений разделов динамики и методов аналитической механики; статика изучается как раздел динамики, а в разделе кинематики подробно вводятся необходимые для раздела динамики понятия и математический аппарат

Статика материальной точки

Рассмотрим материальную точку, которая находится в равновесии. И пусть на нее действуют n
сил ,
k = 1, 2, …,
n
.

Если материальная точка находится в равновесии, то векторная сумма действующих на нее сил равна нулю:(1)
.

В равновесии геометрическая сумма сил, действующих на точку, равна нулю.

Геометрическая интерпретация
. Если в конец первого вектора поместить начало второго вектора ,
а в конец второго вектора поместить начало третьего ,
и далее продолжать этот процесс, то конец последнего, n
-го вектора окажется совмещенным с началом первого вектора. То есть мы получим замкнутую геометрическую фигуру, длины сторон которой равны модулям векторов .
Если все векторы лежат в одной плоскости, то мы получим замкнутый многоугольник.

Часто бывает удобным выбрать прямоугольную систему координат
Oxyz
.
Тогда суммы проекций всех векторов сил на оси координат равны нулю:

Если выбрать любое направление, задаваемое некоторым вектором ,
то сумма проекций векторов сил на это направление равна нулю:.
Умножим уравнение (1) скалярно на вектор :
.
Здесь — скалярное произведение векторов и .
Заметим, что проекция вектора на направление вектора определяется по формуле:.

4. Определение скорости точки при векторном способе задания движения.

Пусть в момент времени
t

положение точки определяется радиусом-вектором , а в момент времени
t

1

– радиусом-вектором , тогда за промежуток времени точка совершит перемещение .

(1.5) средняя скорость точки, направлен вектор также как и вектор

Скорость точки в данный момент времени

Чтобы получить скорость точки в данный момент времени, необходимо совершить предельный переход

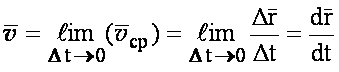(1.6)

(1.7)

Вектор скорости точки в данный момент времени

равен первой производной от радиуса-вектора по времени и направлен по касательной к траектории в данной точке.

(единица измерения
¾
м/с, км/час)

Вектор среднего ускорения

имеет то же направление, что и вектор
Δ

v

, то есть, направлен в сторону вогнутости траектории.

Вектор ускорения точки в данный момент времени

равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.

(еденица измерения — )

Как располагается вектор по отношению к траектории точки?

При прямолинейном движении вектор направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения , также как и вектор ср лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор ср будет направлен в сторону вогнутости траектории и будет лежать в плоскости, проходящей через касательную к траектории в точке
М

и прямую, параллельную касательной в соседней точке
М 1

.

В
пределе, когда точка
М 1

стремится к
М

эта плоскость занимает положение так называемой соприкасающейся плоскости. Следовательно, в общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Общие теоремы динамики системы тел. Теоремы о движении центра масс, об изменении количества движения, об изменении главного момента количества движения, об изменении кинетической энергии. Принципы Даламбера, и возможных перемещений. Общее уравнение динамики. Уравнения Лагранжа.

Работа, которую совершает сила
, равна скалярному произведению векторов силы и бесконечно малому перемещению точки ее приложения :
, то есть произведению модулей векторов F
и ds
на косинус угла между ними.

Работа, которую совершает момент сил
, равна скалярному произведению векторов момента и бесконечно малого угла поворота :
.

Усталостные нагрузки: причины и последствия

В основе возникновения усталостных нагрузок лежит свойство материала ухудшаться при повторном воздействии нагрузки, даже если она ниже его предела прочности. При этом, повреждение материала может наблюдаться даже при незначительных величинах нагрузки, которые иногда могут быть ниже его предела упругости. Таким образом, усталостная прочность материала значительно ниже его прочности при кратковременных нагрузках.

Причины возникновения усталостных нагрузок могут быть различными. Одной из основных причин является агрессивная среда, в которой работает конструкция. Воздействие химических веществ, абразивных и коррозионных факторов может привести к ускоренному разрушению материала и увеличению усталостных нагрузок.

Также необходимо учитывать вибрации и динамические нагрузки, которые могут вызывать микротрещины и малоцикловое разрушение материала. Неравномерное распределение напряжений, резкое изменение нагрузки и повышенная температура также могут являться причинами повышенной усталостной нагрузки на материал.

Последствия от длительного воздействия усталостных нагрузок могут быть катастрофическими. Разрушение материала может происходить без видимых признаков повреждения, что является особенно опасным. Это может привести к серьезным поломкам и авариям в различных инженерных системах, таких как мосты, самолеты, автомобили, машины и другие.

Для предотвращения таких последствий необходимо проводить тщательную оценку и учет усталостных нагрузок при разработке конструкций. Расчет прочности и продолжительности работы материала при усталостных нагрузках позволяет предотвратить разрушение и обеспечить надежность и безопасность конструкции.

Кинематика

Раздел кинематики отвечает на вопросы о том, как именно происходит механическое движение тела.

Механическое движение 

Механическое движение — это перемещение тела с течением времени и относительно других объектов в пространстве. 

Для расчета этих изменений понадобится система отсчета, которая состоит из:

• объекта, относительно которого будет происходить отсчет движения;
• системы координат, в которой находится объект отсчета;
• часов (для измерения времени).

В системе отсчета метр является единицей длины, а секунда — единицей времени.

Другими важными определениями в кинематике являются:

1. Материальная точка — это объект, размеры которого можно не учитывать в расчетах.  
2. Траектория движения тела (линия, по которой движется объект).
3. Путь, пройденный телом (определенный участок траектории, пройденный объектом за определенное время).

Существует 2 вида движения согласно траектории:

• прямое;
• криволинейное.

Поступательное и вращательное движение твердого тела

В кинематике выделяют два вида движения:

• поступательное;
• вращательное.

Поступательное движение — это движение твердого тела, при котором все его точки проходят одну и ту же траекторию и в любой момент времени обладают одинаковыми по направлению и величине векторами скорости и ускорения, синхронно меняющихся для любой точки объекта.

Вращательное движение — это вид механического движения, при котором материальное тело проходит траекторию окружности. При этом все точки тела описывают окружности, которые находятся в параллельных плоскостях. Центры всех окружностей находятся на одной прямой, которая перпендикулярна к плоскостям окружностей (называется осью вращения).

Кинематические уравнения движения

Определение местоположения материальной точки в пространстве можно осуществить двумя способами:

• учитывая зависимость координат от времени;
• учитывая зависимость от времени радиус-вектора.

Эту зависимости можно представить в виде кинематических уравнений движения:

\(x=x\left(t\right) \)

\(y=y\left(t\right)\)

\(z=z\left(t\right)\)

или 

\(\vec r=\vec r\left(t\right)\)

Нулевой вектор на данной иллюстрации — это радиус-вектор положения точки в начальный момент времени.

Кинематические характеристики (скорость, ускорение)

Основными кинематическими характеристиками являются:

• скорость;
• ускорение.

Скорость \((\vec v)\) — это векторная величина, которая характеризует направление и быстроту движения.

Среднюю скорость можно вычислить по формуле:

\(\vec v=\frac{\Delta\vec r}{\Delta t}\)

где \(\Delta\vec r \) — перемещение, \(\Delta t\) — время, за которое это перемещение произошло.

Символом \(∆\) обозначается разность однотипных величин или совсем маленьких интервалов.

Мгновенная скорость может быть вычислена тогда, когда \(\Delta t\rightarrow0\) и вектор перемещения совпадает с путем перемещения:

\(\vec v=\frac{d\vec r}{dt}=\frac{dS}{dt}\)

Ускорение тела (a) является величиной, равной отношению изменения скорости движения тела к длительности промежутка времени, за которое это изменение скорости произошло. Оно рассчитывается по формуле:

\(a=\frac{\Delta V}{\Delta t}\)

Мгновенным ускорение будет являться тогда, когда среднее ускорение за промежуток ∆t → 0, м/с²:

\(a=\frac{dv}{dt}\)

Что такое движение?

Именно после этого определения мы совершенно естественно приходим к понятию системы отсчета. Изменение положения тел в пространстве относительно друг друга.
Ключевые слова здесь: относительно друг друга

. Ведь пассажир в машине движется относительно стоящего на обочине человека с определенной скоростью, и покоится относительно своего соседа на сиденье рядом, и движется с какой-то другой скоростью относительно пассажира в машине, которая их обгоняет.

Именно поэтому, для того, чтобы нормально измерять параметры движущихся объектов и не запутаться, нам нужна система отсчета — жестко связанные между собой тело отсчета, система координат и часов.

Например, земля движется вокруг солнца в гелиоцентрической системе отсчета. В быту практически все свои измерения мы проводим в геоцентрической системе отсчета, связанной с Землей. Земля – тело отсчета, относительно которого движутся машины, самолеты, люди, животные.

Механика, как наука, имеет свою задачу. Задача механики – в любой момент времени знать положение тела в пространстве.

Иными словами, механика строит математическое описание движения и находит связи между физическими величинами, его характеризующими.

Для того, чтобы двигаться далее, нам понадобится понятие “материальная точка

”. Говорят, физика – точная наука, но физикам известно, сколько приближений и допущений приходится делать, чтобы согласовать эту самую точность. Никто никогда не видел материальной точки и не нюхал идеального газа, но они есть! С ними просто гораздо легче жить.

Работа и механическая энергия

Энергия — это способность физических объектов совершать определенную работу, поэтому количественно работа и энергия измеряются в одних и тех же единицах — джоулях (Дж).

Механическая работа будет численно равна изменениям механической энергии. Работа в механике бывает постоянной и переменной силы.

Работа постоянной и переменной силы

Сила, воздействующая на тело, когда перемещает его на определенное расстояние, совершает работу. В том случае, когда сила постоянна по величине и направлению, а движение прямолинейно, можно говорить о работе постоянной силы.

Если траектория движения объекта не прямолинейна, а сила, действующая на тело, не является постоянной, нужно говорить о работе переменной силы. Чтобы ее рассчитать, необходимо весь путь разбить на прямолинейные отрезки. Полная работа будет в таком случае равна сумме работ на всех прямолинейных участках.

Энергия

Энергия — это скалярная величина, которая является количественной мерой различных форм движения материи. Энергия, которая является мерой механического движения и механического взаимодействия тел с другими объектами и между собой, называется механической.

Изменение механической энергии системы (\(\Delta W\)) определяется работой (\(A\)), которую совершают внешние силы, воздействующие на систему:

\(\Delta W=A\)

Механическая энергия бывает двух видов:

• кинетической;
• потенциальной.

Кинетическая

Кинетическая энергия — это скалярная функция, которая является количественной мерой движения материальных тел, рассматриваемых в конкретной механической системе. Кинетическая энергия зависит только от массы (\(m\)) и модуля скорости материальной точки (\(v\)).

Рассчитывается кинетическая энергия (\(E\)) по формуле:

\(E=\frac{m\times v^2}2\)

Измеряется в джоулях.

Потенциальная 

Потенциальная энергия — это физическая величина, которая обозначает энергию взаимодействия тел или их частей между собой. Потенциальная энергия зависит только от расстояния, на котором находятся объекты. Имеет числовое значение, но не имеет вектора направления. 

Потенциальной энергией обладают следующие виды тел: 

• объекты, находящиеся на какой-либо высоте от поверхности земли;
• упруго деформированные тела (пружина);
• сжатые газы.

Потенциальная энергия тела, поднятого над землей (\(E\)), рассчитывается по формуле:

\(E=m\times g\times h\)

где \(m\) — масса тела, \(h\) — высота над землей, \(g\) — ускорение свободного падения на нашей планете.

Потенциальная энергия упруго деформированного тела (\(E\)) определяется по формуле:

\(E=\frac{k\times x^2}2\)

где \(x\) — удлинение, \(k\) — жесткость.

Потенциальная энергия измеряется в джоулях.

Закон сохранения механической энергии

Закон сохранения энергии в механике известен всем со школы.

Энергия не исчезает и не возникает снова, она только переходит из одного вида энергии в другой или передается от одного объекта к другому.

Статические нагрузки в сопротивлении материалов

В сопротивлении материалов статические нагрузки классифицируются по типу действующей силы. Различают сжимающие, растягивающие, сдвиговые, изгибные и крутящие нагрузки. Каждый тип нагрузки оказывает различное воздействие на материал и требует специального подхода в процессе проектирования и расчета конструкции.

Сжимающие нагрузки приводят к сжатию материала и оцениваются посредством рассмотрения его сопротивления сжатию. Растягивающие нагрузки, наоборот, вызывают растяжение материала и требуют учета его сопротивления растяжению. Сдвиговые нагрузки возникают, когда сила действует параллельно плоскости материала, и оцениваются посредством рассмотрения его сдвигового сопротивления.

Изгибные нагрузки возникают, когда сила действует перпендикулярно к оси материала. Они приводят к появлению изгибающих моментов, которые требуют учета его искривления и изгибного сопротивления. Крутящие нагрузки вызывают вращение материала и требуют учета его крутящего сопротивления.

В зависимости от нагрузки и типа материала необходимо выбирать соответствующий метод расчета и применять соответствующие формулы. Это позволяет гарантировать безопасность и надежность конструкции.

Общие сведения

Достижения технической механики позволяют не только улучшать кон­струкции машин и механизмов, но и совершенствовать производственные процессы. Сегодня на многих предприятиях широко используются маши­ны-автоматы, автоматические поточные линии, которые без прямого учас­тия человека обеспечивают выпуск готовой продукции, начиная с обработ­ки сырья и кончая упаковкой готовых изделий.

Область применения законов механики для решения конкретных техни­ческих задач очень обширна. Наша эпоха научно-технического прогресса с особенной силой подтверждает необозримость практического приложения этой науки.

Техническая механика — это наука об общих законах меха­нического движения и применения их в современной технике.

Техническая механика состоит из двух частей: теоретичес­кой и прикладной. Первая часть посвящена изучению теоретических основ механического движения, вторая — использованию положений теоретиче­ской механики для практических целей: проектирования механизмов, рас­чета деталей машин, строительных конструкций и сооружений.

Теоретическую механику принято подразделять на три тесно связанных раздела: статику, кинематику и динамику (рис. 1). В за­дачи теоретической механики входит определение условий, при которых соблюдаются условия равновесия тел. Этот раздел механики называют статикой. Изучением движения тел на основании законов геометрии занимается раздел механики, называемый кинематикой. Раздел ме­ханики, в котором изучается движение тел и рассматриваются причины, его вызвавшие, называют динамикой. Статика, кинематика и динами­ка охватывают все вопросы, связанные с механическим движением тел, и позволяют решать многочисленные практические задачи.

Понятие «тело» является обобщающим. В механике под телом принято понимать все предметы окружающего нас мира: строения, оборудование це­хов заводов, лабораторий и т. д. Твердое тело — физическое тело, характеризующееся стабильностью формы. Механическим движением тела называется изменение его положения по отношению к другим телам с течением времени.

Прикладная механика также состоит из трех крупных разделов: тео­рии механизмов и машин, сопротивления материалов, деталей машин.

В «Теории механизмов и машин» на основании законов теоретической механики рассматриваются принципы анализа и проектирования механиз­мов, «Сопротивление материалов» позволяет установить условия прочнос­ти и устойчивости проектируемых конструкций и сооружений. «Детали ма­шин» посвящены изучению принципов расчета и конструирования деталей и сборочных единиц машин общего назначения.

Последовательное изучение всех этих разделов и является предметом технической механики.

cherch.ru

Классификация нагрузок | Строительный справочник

Как показывает практика, тема сбора нагрузок вызывает наибольшее количество вопросов у молодых инженеров, начинающих свою профессиональную деятельность.

В данной статье хочу рассмотреть, что такое постоянные и временные нагрузки, чем длительные нагрузки отличаются от кратковременных и для чего такое разделение необходимо и т.п.

Как следует из самого названия, постоянные нагрузки действуют на всем протяжении эксплуатации. Временные нагрузки проявляются в отдельные периоды строительства или эксплуатации.

К постоянным нагрузкам относятся: собственный вес несущих и ограждающих конструкций, вес и давление грунтов. В случае применения в проекте конструкций заводского изготовления (ригели, плиты, блоки и т.п.

), нормативное значение их веса определяется на основании стандартов, рабочих чертежей или паспортных данных заводов — изготовителя.

В прочих случаях вес конструкций и грунтов определяется по проектным данным на основании их геометрических размеров как произведение их плотности ρ на объем V с учетом их влажности в условиях возведения и эксплуатации сооружений.

Ориентировочные плотности некоторых основных материалов приведены в табл. 1. Ориентировочные веса некоторых рулонных и отделочных материалов приведены в табл. 2.

Таблица 1

Вес рулонных и отделочных материалов

Временные нагрузки подразделяются на длительные, кратковременные и особые.

К длительным нагрузкам относятся:

— нагрузка от людей, мебели, животных, оборудования на перекрытия жилых, общественных и сельскохозяйственных зданий с пониженными нормативными значениями;

— нагрузки от автотранспорта с пониженными нормативными значениями;

— вес временных перегородок, подливок и подбетонок под оборудование;

— снеговые нагрузки с пониженными нормативными значениями;

— вес стационарного оборудования (станки, моторы, емкости, трубопроводы, жидкости и твердые тела, заполняющие оборудование);

— давление газов, жидкостей и сыпучих тел в емкостях и трубопроводах, избыточное давление и разряжение воздуха, возникающее при вентиляции шахт;

— нагрузки на перекрытия от складируемых материалов и стелажного оборудования в складских помещениях, холодильниках, зернохранилищах, книгохранилищах, архивах подобных помещениях;

— температурные технологические воздействия от стационарного оборудования;

— вес слоя воды на водонаполненных плоских покрытиях;

— вертикальные нагрузки от мостовых и подвесных кранов с пониженным нормативным значением, определяемым умножением полного нормативного значения вертикальной нагрузки от одного крана в каждом пролете здания на коэффициент:

0,5 — для групп режимов работы кранов 4К-6К;

0,6 — для группы режима работы кранов 7К;

0,7 — для группы режима работы кранов 8К.

Группы режимов кранов принимаются по ГОСТ 25546.

К кратковременным нагрузкам относятся:

— вес людей, ремонтных материалов в зонах обслуживания и ремонта оборудования с полными нормативными значениями;

— нагрузки от автотранспорта с полными нормативными значениями;

— снеговые нагрузки с полными нормативными значениями;

— ветровые и гололедные нагрузки;

— нагрузки от оборудования, возникающие в пускоостановочном, переходном и испытательном режимах, а также при его перестановке или замене;

— температурные климатические воздействия с полным нормативным значением;

— нагрузки от подвижного подъемно — транспортного оборудования (погрузчиков, электрокаров, кранов — штабелеров, тельферов, а также от мостовых и подвесных кранов с полным нормативным значением).

К особым нагрузкам относятся:

— сейсмические воздействия;

— взрывные воздействия;

— нагрузки, вызываемые резкими нарушениями технологического процесса, временной неисправностью или поломкой оборудования;

— воздействия, обусловленные деформациями основания, сопровождающимися коренным изменением структуры грунта ( при замачивании просадочных грунтов) или оседанием его в районах горных выработок и в карстовых.