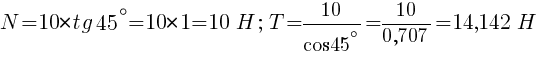Пара сил

Теория пар сил

Пару сил в механике рассматривают как одно из основных понятий наряду с понятием силы.
Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны. Пара сил не составляет системы сил, эквивалентной нулю. Пару сил нельзя заменить одной силой, и, следовательно, она не имеет равнодействующей, а является такой системой сил, упростить которую нельзя. Каждая из сил, входящих в состав пары сил, имеет свойства обычных сил.

Пара сил, действующая на твердое тело, характеризуется, прежде всего, плоскостью действия. Плоскостью действия пары сил называют плоскость, в которой расположены силы пары.

Силы, направленные в одну сторону

Пусть в абсолютно твердого тела в точках А и В приложены две параллельные силы и направленные в одну сторону (рис. 4.1). Найдем их равнодействующую. Для этого в точках А и В к телу приложим две равные по величине и противоположные по направлению силы и, действующих по прямой АВ.

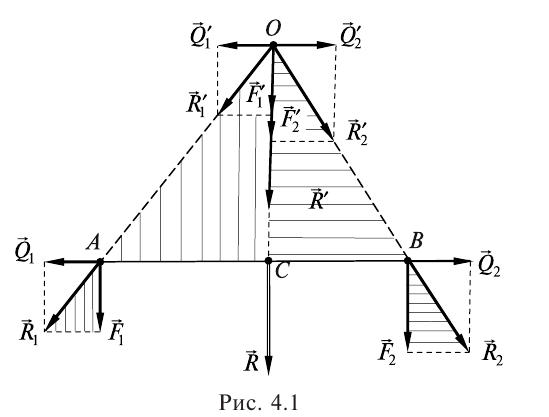
Поскольку , то согласно первой аксиомой статики , а согласно второй аксиомой . Добавляя попарно силы и , и , используя аксиому параллелограмма сил, получим:

 то есть 

 то есть 

Итак, 

Силы  и  не является параллельными лежат в одной плоскости, поэтому их линии
действия имеют точку пересечения А. Перенесем силы  и   вдоль их линий действия в эту точку. Получим силы

Сила — скользящий вектор, поэтому  Разложим теперь силу  на составляющие , а силу — на составляющие так, чтобы: 

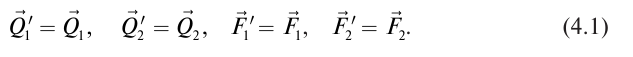
Получим:

 

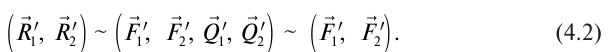
Поскольку силы  и  направлены по одной прямой в одну сторону, то их равнодействующая  cпрямована по той же прямой в том же направлении и ее величина равна сумме этих сил, то есть Учитывая (4.1), запишем Перенесем силу вдоль линии ее действия в точку С отрезка АВ. Получим силу Это означает, что сила — равнодействующая сил  

Найдем точку приложения равнодействующей сил и . С сходства одинаково заштрихованных треугольников запишем:

 и 

Поскольку, то, откуда, учитывая свойство пропорции, имеем

Итак, равнодействующая двух параллельных сил, направленных в одну сторону, параллельна этих сил, направленная в ту же сторону, что и составляющие силы; модуль
равнодействующей равна сумме модулей составляющих сил, а линия ее действия разделяет расстояние между точками приложения этих сил внутри на части, обратно
пропорциональны величинам этих сил.

Из изложенного следует, что произвольную силу можно разложить на две параллельные силы. Если то

Силы направлены в противоположные стороны и различные по модулю

Пусть параллельные силы  и направлены в разные стороны  и (рис. 4.2). 

Найдем равнодействующую сил и  Для этого разложим силу на две параллельные силы: , прилагаемую в точке В, принимая  и  , прилагаемую в точке С. Сила является равнодействующей сил и поэтому

Согласно  (4.3), откуда

Поскольку Но  поэтому  Следовательно, сила — равнодействующая сил  Из формулы (4.4) получим 

Равнодействующая двух параллельных, разных по модулю, противоположно направленных сил параллельная им и направлена в сторону большей силы; модуль равнодействующей равна разности модулей составляющих сил. Линия действия равнодействующей проходит через точку, лежащую вне отрезка АВ со стороны большей силы и разделяет расстояние между точками приложения сил внешне на отрезки, обратно пропорциональны величинам этих сил.

Условия равновесия пар сил.

Лекция 4

ПАРА СИЛ

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Плоскостью действия пары сил называется плоскость в которой расположены эти силы.

Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.

Моментом пары сил называется вектор , модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.

Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.

Доказательство: Выберем произвольно точку О. Проведем из нее в точки А и В радиус-векторы (Смотри Рис. 4.2).

,

Что и требовалось доказать.

Рис. 4.2

Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.

Доказательство: Пусть на твердое тело действует пара сил .

Перенесем силу в точку , а силу в точку . Проведем через точки две любые параллельные прямые, пересекающие линии действия сил пары. Соединим точки отрезком прямой и разложим силы в точке и в точке по правилу параллелограмма.

Так как , то

и

Поэтому эквивалентна системе , а эта система эквивалентна системе , так как эквивалентна нулю.

Таким образом мы заданную пару сил заменили другой парой сил . Докажем, что моменты у этих пар сил одинаковы.

Момент исходной пары сил численно равен площади параллелограмма , а момент пары сил численно равен площади параллелограмма . Но площади этих параллелограммов равны, так как площадь треугольника равна площади треугольника .

Что и требовалось доказать.

1. Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.

2. У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.

Теорема о переносе пары сил в параллельную плоскость.Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.

Доказательство: Пусть на твердое тело действует пара сил в плоскости . Из точек приложения сил А и В опустим перпендикуляры на плоскость и в точках их пересечения с плоскостью приложим две системы сил и , каждая из которых эквивалентна нулю.

Сложим две равные и параллельные силы и . Их равнодействующая параллель-на этим силам, равна их сумме и приложена посредине отрезка в точке О.

Сложим две равные и параллельные силы и . Их равнодействующая параллель-на этим силам, равна их сумме и приложена посредине отрезка в точке О.

Так как , то система сил эквивалентна нулю и ее можно отбросить.

Таким образом пара сил эквивалентна паре сил , но лежит в другой, параллельной плоскости. Что и требовалось доказать.

Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.

Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.

Теорема о сложении пар сил.Две пары сил, действующих на одно и то же твердое тело, и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Доказательство: Пусть имеются две пары сил, расположенные в пересекающихся плоскостях. Пара сил в плоскости характеризуется моментом , а пара сил в плоскости характеризуется моментом .

Расположим пары сил так, чтобы плечо пар было общим и располагалось на линии пересечения плоскостей. Складываем силы, приложенные в точке А и в точке В, . Получаем пару сил .

Что и требовалось доказать.

Условия равновесия пар сил.

Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Теорема.Для равновесия пар сил, приложенных к твердому телу, необхо-димо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.

Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.

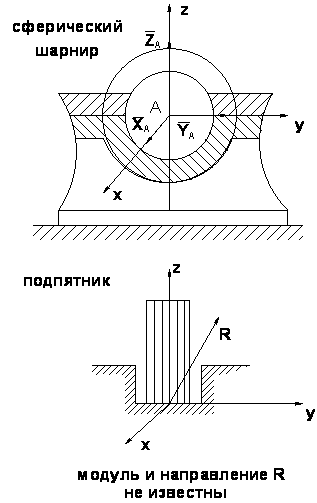
2. Связи и их реакции

Твердое тело называется свободным
, если оно может перемещаться в пространстве в любом направлении.

Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью
.

Твердое тело, свобода движения которого ограничено связями, называется несвободным
.

Все силы, действующие на несвободное твердое тело, можно разделить на:

• задаваемые (активные)
  
• реакции связей
  

Задаваемая сила

выражает действие на данное тело других тел, способных вызвать изменение его кинематического состояния.

Реакция связи

– это сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям.

Принцип освобождаемости твердых тел от связей

— несвободное твердое тело можно рассматривать как свободное, на которое кроме задаваемых сил, действуют реакции связей.

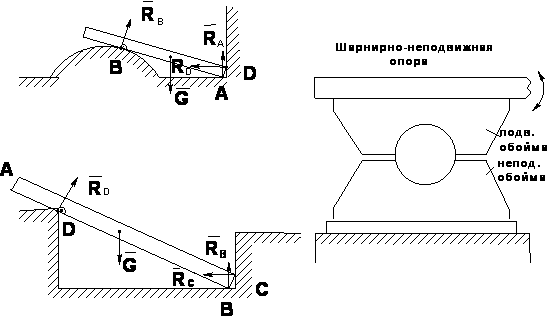
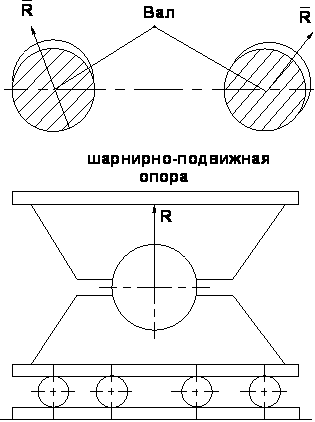
Как определить направление реакции?

Если существует два взаимно перпендикулярных направления на плоскости, в одном из которых связь препятствует перемещению тела, а в другом нет, то направление ее реакции противоположно первому направлению.

В общем случае направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу.

	Неподвижный шарнир Подвижный

iSopromat.ru

Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:

Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия: R=0, M_O=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

Слайд 8Пьер ВариньонПьер Вариньон (фр. Pierre Varignon, Кан, 1654 — 23 декабря, 1722,

Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа

Мазарини (1688), профессор Коллеж де Франс. Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году.Вариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением Лопиталя, Вариньон был самым первым пропагандистом дифференциального исчисления во Франции. В 1687 году в своей работе «Проект новой механики…» Вариньон дал точную формулировку закона параллелограмма сил, развил понятие момента сил и вывел теорему, получившую имя Вариньона. В работе «Новая механика или статика, проект которой был дан в 1687» (1725) Вариньон дал систематическое изложение учения о сложении и разложении сил, о моментах сил и о правилах оперирования ими.

Формы условий равновесия

Первая форма

Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:

причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.

Вторая форма

Уравнения равновесия могут быть записаны иначе:

Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.

Третья форма

Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.

Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.

Сложение пар сил. Условие равновесия системы пар сил.

Теорема
о сложении пар сил:

Две
пары сил, произвольно расположенные в
пространстве, эквивалентны одной паре
с моментом равным геометрической сумме
моментов слагаемых пар.

Если
на тело действует произвольная система
(М1,М2,…,Мn)
пар, то вектор момента результирующей
пары равен векторной сумме моментов,
составляющих пары. M=M1+M2+…+Mn=ΣMk
(сверху векторы)

Если
две пары сил расположены в одной
плоскости, то векторы моментов пар
направлены перпендикулярно этой
плоскости в ту или иную стороны. Поэтому
моменты пар можно складывать алгебраически.
M=M1+M2+…+Mn=ΣMk

Условие
равновесия системы пар сил:

Для
равновесия тела, находящегося под
действием системы произвольно
расположенных в пространстве пар,
необходимо и достаточно, чтобы момент
результирующей (эквивалентной) пары
был равен 0.

В
случае, если все пары сил расположены
в одной плоскости (или в параллельных
плоскостях), то для равновесия необходимо
равенство 0 алгебраической суммы моментов
составляющих пар.

Слайды и текст этой презентации

Слайд 1ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

СТАТИКАЛекция №2

BOmr

Слайд 8Пьер ВариньонПьер Вариньон (фр. Pierre Varignon, Кан, 1654 — 23 декабря, 1722,

Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа

Мазарини (1688), профессор Коллеж де Франс. Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году.Вариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением Лопиталя, Вариньон был самым первым пропагандистом дифференциального исчисления во Франции. В 1687 году в своей работе «Проект новой механики…» Вариньон дал точную формулировку закона параллелограмма сил, развил понятие момента сил и вывел теорему, получившую имя Вариньона. В работе «Новая механика или статика, проект которой был дан в 1687» (1725) Вариньон дал систематическое изложение учения о сложении и разложении сил, о моментах сил и о правилах оперирования ими.

Слайд 102.2 Теория пар сил,
свойства пар сил

Слайд 17Пуансо Луи
Пуансо (Poinsot) Луи (3.1.1777, Париж, — 5.12.1859, там же),

французский математик и механик, член Парижской АН с 1813. Окончил

Политехническую школу в Париже (1797), с 1809 профессор там же. В период Июльской монархии — в Министерстве народного образования. Пэр Франции (1846), сенатор (1852). Первые работы П. посвящены теории правильных звездчатых многогранников. В 1803 опубликовал «Элементы статики», в которых применил разработанные им геометрические методы исследования к учению о равновесии твёрдых тел и их систем. В 1834 построил теорию вращения твёрдого тела вокруг неподвижной точки. Впервые ввёл понятие эллипсоида вращения.

Слайд 18Теорема1 — О параллельном переносе силы
(лемма Пуансо):силу ,

не изменяя ее действия на абсолютно твердое тело, можно переносить

из данной точки А в любую другую точку О тела, прибавляя при этом пару с моментом равным моменту переносимой силы относительно точки О, в которую переносится сила .

Слайд 21Теорема 2 – О приведении системы сил к заданному центру

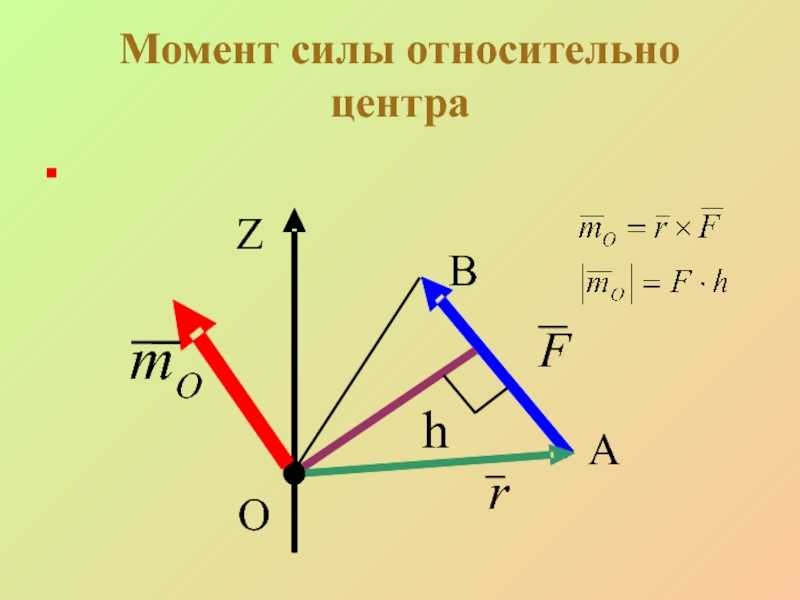
(теорема Пуансо):Любая система сил , действующая на абсолютно твердое тело,

при приведении к произвольному центру О заменяется главным вектором системы сил, приложенным в центре О и парой сил с моментом , равным главному моменту системы сил относительно центра О.

Слайд 24Используя теорему 1 перенесем все силы в центр О прибавляя

пары с моментами равными моментам сил относительно центра О. Сложив

все силы и моменты получим в центре О два вектора и равные:

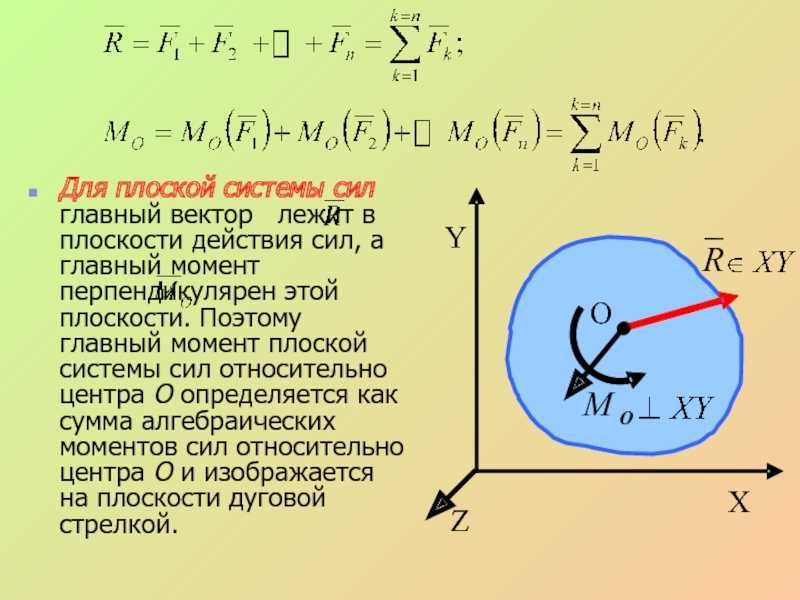
Слайд 25Для плоской системы сил главный вектор лежит в плоскости

действия сил, а главный момент  перпендикулярен этой плоскости. Поэтому

главный момент плоской системы сил относительно центра О определяется как сумма алгебраических моментов сил относительно центра О и изображается на плоскости дуговой стрелкой.

X

Y

O

Z

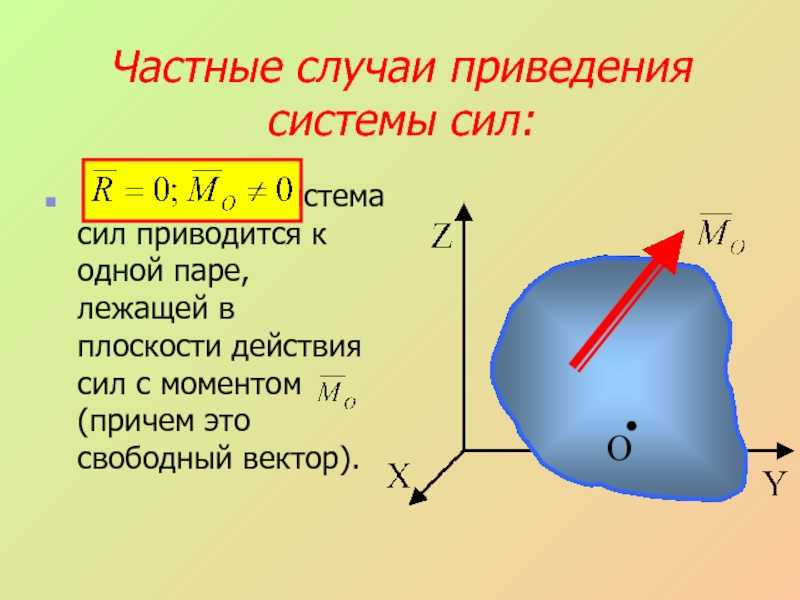
система сил приводится к одной паре,

лежащей в плоскости действия сил с моментом (причем это свободный вектор).

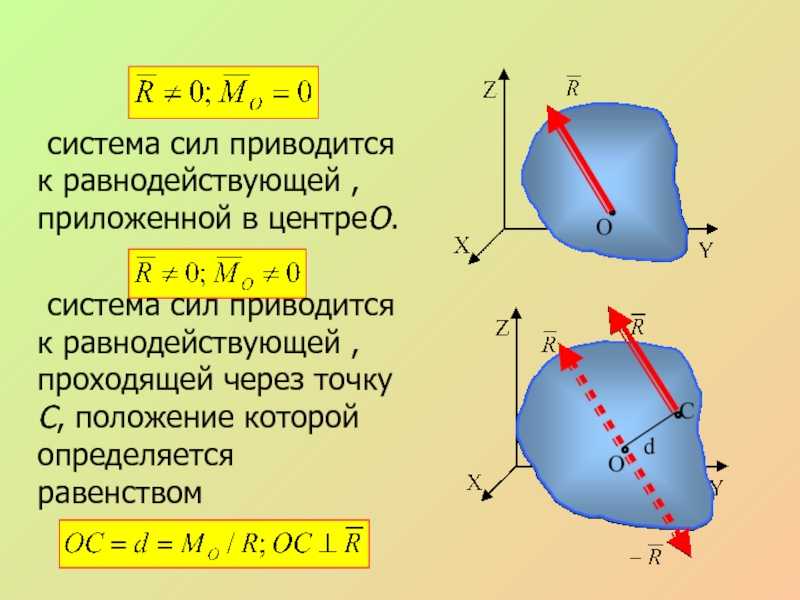
Слайд 27 система сил приводится к равнодействующей , приложенной в центреО.  система сил

определяется равенством

Слайд 28 система сил уравновешена. Теорема: Для равновесия любой системы сил

необходимо и достаточно, чтобы главный вектор и главный момент этой

системы относительно любого центра (точки) были равны нулю.

твердого тела, находящегося под действием произвольной плоской системы сил в

векторной форме имеют вид Из этих векторных уравнений следуют три формы аналитических условий равновесия.

Слайд 30Основная форма условий равновесиядля сил, лежащих в плоскости ОХУ:Для равновесия

произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций

сил на каждую из координатных осей и сумма моментов сил относительно любой точки, лежащей в плоскости действия сил, были равны нулю.

и достаточно, чтобы суммы моментов всех сил относительно двух точек

А и В и сумма их проекций на ось ОX, не перпендикулярную прямой АВ, были равны нулю.

и достаточно, чтобы суммы моментов всех сил относительно любых трех

точек А, В и С, не лежащих на одной прямой, были равны нулю. 

Слайд 35 Для проверки решения задачи на равновесие плоской системы сил

в масштабе многоугольник всех сил, действующих на тело. Если проверочное уравнение обращается в тождество, а многоугольник сил замкнут, то задача решена верно.

Примеры решения задач

Решение примеров по теме: «Статика твердого тела»

Пример 1. Условия
равновесия

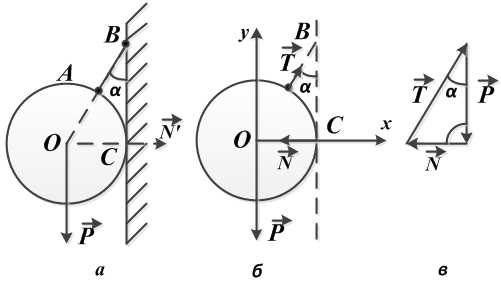
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в
десять Ньютон, находится в состоянии равновесия (рис.а).
Необходимо определить давление однородного шара на гладкую стенку и натяжение
нити.

Дано:P= 10 Н;α= 45°Найти:N,
T — ?

Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенкиNнаправлена перпендикулярно стенке (от
точки касанияСк центру шараО),
реакция нитиТ— вдоль нити от точкиАк точкеВ.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.

Это система сил, сходящихся в центреОшара, и состоящая из веса шараР(активная сила), реакции стенкиNи реакции нитиТ(рис.б).

РеакцииNиТпо величине неизвестны. Для их
определения следует воспользоваться условиями равновесия (в той или иной форме
— геометрической, аналитической).

При
геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема
синусов, теорема косинусов, теорема Пифагора и т.д.).

В данном случае это замкнутый силовой треугольник (рис.в),
из которого получаем:

После
подстановки в формулы числовых значений, получим:.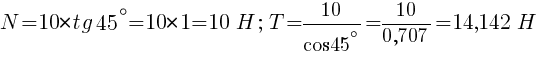

Ответ:.

Решение примеров по теме: «Кинематика»

Пример 2. Уравнение
траектории точки

Дано:
Движение точки задано уравнениями;
(x, у— в сантиметрах,t— в секундах).Найти:уравнение траектории точки в
координатной форме.

Решение.Для
определения уравнения траектории из уравнений движения исключаем времяt.
Для этого из первого уравнения выражаеми подставляем это значение во второе
уравнение, преобразованное к функциям одинарного угла:.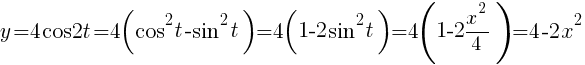

Опуская
промежуточные выражения, получаем уравнение траектории:.

Уравнение определяет параболу,
расположенную симметрично относительно осиу, с вершиной в точке (0, 4).
Траекторией служит кусок этой параболы, заключенный между точками с
координатами (-2, -4) и (2, -4).

Ответ:.

Решение примеров по теме: «Динамика»

Пример 3. Основной
закон динамики точки

Свободная
материальная точка, масса которой десять килограмм, движется прямолинейно с
ускорением пол метра в секунду в квадрате. Определить силу, приложенную к
точке.

Дано:m= 10 кг;a= 0,5 м/с2.Найти:F
— ?

Решение.
Согласно основному закону динамики:.

Подставив
значения в формулу, получим:

Ответ:сила,
сообщающая массе, равной 10 кг,
ускорение 0,5 м/с2, равна 5
Н.

В ПОМОЩЬ СТУДЕНТУ

Формулы,
правила, законы, теоремы, уравнения, примеры решения задач

·Теоретические основы электротехники

·Электрические машины

·Высшая математика

Список
литературы:

Бать М.И., Джанелидзе
Г.Ю., Кельзон А.С. Теоретическая механика в примерах
и задачах.Буторин Л.В., Бусыгина Е.Б. Теоретическая механика.
Учебно-практическое пособие.

Момент силы относительно оси

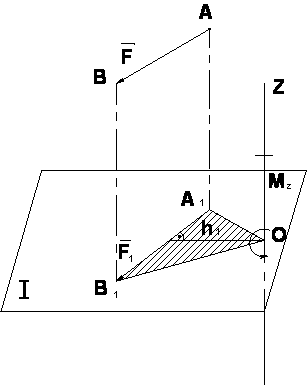
Чтобы определить момент силы относительно оси необходимо:

1) провести плоскость, перпендикулярную к оси Z;

2) определить точку О
пересечения оси с плоскостью;

3) спроецировать ортогонально силу F
на эту плоскость;

4) найти момент проекции силы F
относительно точки О пересечения оси с плоскостью.

Правило знаков:

Момент силы относительно оси считается положительным
, если, смотря навстречу оси Z,
можно видеть проекцию , стремящейся вращать плоскость I

вокруг оси Z в сторону, противоположную вращению часовой стрелки.

Свойства момента силы относительно оси 1) Момент силы относительно оси изображается отрезком, отложенным по оси Zот точки О в положительном направлении, если > 0 и в отрицательном направлении, если 2) Значение момента силы относительно оси может быть выражено удвоенной площадью Δ (1.5) 3) Момент силы относительно оси равен нулю в двух случаях: если F 1 = 0 , то есть линия действия силы параллельна оси; eсли h 1 = 0 , то есть линия действия силы пересекают ось.

Основные понятия и определения статики.

Материальные объекты в статике:

система материальных точек,

абсолютно твердое тело.

Системой материальных точек, или механической системой, называется такая совокупность материальных точек, в которой положение и движение каждой точки зависит от положения и движения других точек этой системы.

Абсолютно твердое тело – это тело, расстояние между двумя точками которого не изменяется.

Твердое тело может находиться в состоянии покоя или движения определенного характера. Каждое их этих состояний будем называть кинематическим состоянием тела .

Сила — мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия.

Сила может быть приложена в точке, тогда эта сила – сосредоточенная.

Сила может действовать на все точки данного объема или поверхности тела, тогда эта сила – распределенная.

Система сил — совокупность сил, действующих на данное тело.

Равнодействующей называется сила, эквивалентная некоторой системе сил.

Уравновешивающей силой называется сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону.

Системой взаимно уравновешивающихся сил называется система сил, которая будучи приложенной к твердому телу, находящемуся в покое, не выводит его из этого состояния.

Внутренние силы – это силы, которые действуют между точками или телами данной системы.

Внешние силы – это силы, которые действуют со стороны точек или тел, не входящих в данную систему.