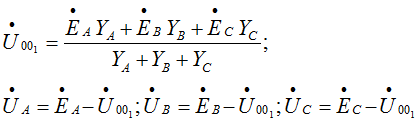Электротехника

3.3. Соединение трехфазной цепи треугольником

При этом начало каждой обмотки соединяется с концом другой.

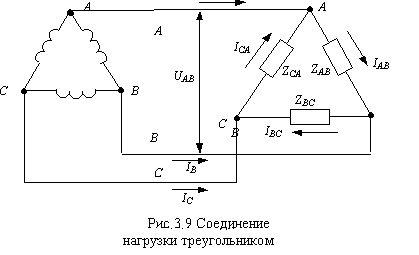
1.Токи в соединительных проводах – линейные токи: I_A,
I_B ,I_C

2.Токи в нагрузках – фазные токи: I_AB, I_BC,
I_CA

3.Напряжения на нагрузках – фазные напряжения.

4.Напряжения между соединительными проводами – линейные напряжения.

При соединении треугольником U_Л=U_Ф I
_Л =
I _Ф

Активная мощность    Р=Р_А+Р_В+Р_С

Реактивная мощность Q=Q_A+Q_B+Q_C

Полная мощность        S=S_A+S_B+S_C

В симметричной 3х-фазной цепи:

P_A=P_B=P_C

Q_A=Q_B=Q_C

S_A = S_B = S_C поэтому

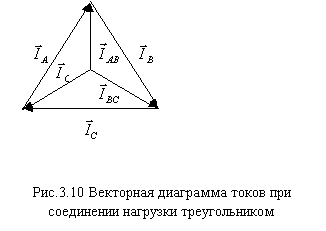
P=3P_Ф=3I_ФU_Фcosf

Q=3Q_Ф=3I_ФU_Фsin
f

S=3S _Ф=3I_ФU_Ф

Измерения фазных напряжений и токов неудобно, т.к. необходим доступ
к нулевому проводу. Проще измерить линейные напряжения и токи на клеммах
потребителя.

P =
U _Л I _Л cos f

Q =
U _Л I _Л sin f

S==

Коэффициент мощности : cosf
=P/S

При выборе схемы соединения нагрузки (звезда, звезда с ноль-проводом,
треугольник) необходимо учитывать следующие факторы :

1.Характер нагрузки.

2.Номинальное напряжение сети.

3.Номинальное напряжение потребителя.

Пример : U _сети =380В, U _лампы
=220В, фазное напряжение равно U_Ф=380/=220.
Лампа соединяется на фазное напряжение, для этого используется соединение
звездой, причем необходим нулевой провод, т.к. нагрузка может оказаться
несимметричной.

Построение диаграммы

Векторная диаграмма предполагает в своей основе следующие значения:

1. Точку начала отсчета N для всех трех отдельных фаз.
2. Векторное направление ABC как отдельных проводников источника напряжения (генератора). Каждый вектор имеет заданную длину, равную своему напряжению.
3. Окончание векторов AВ, BС, CА, как приемников напряжения.

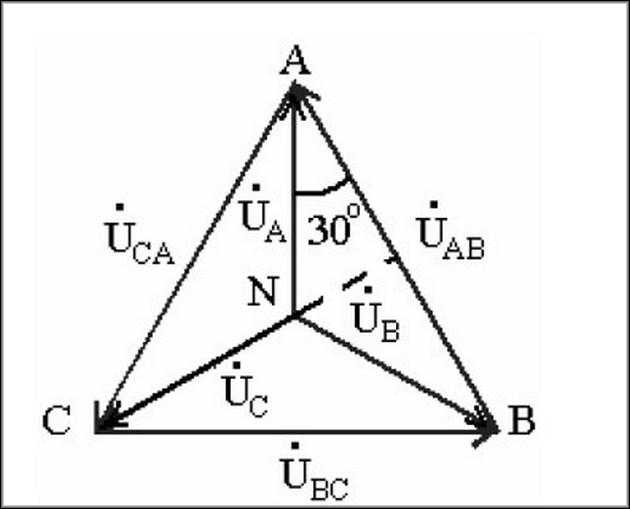
Данные значения дополняются единицей времени, за которое ток, под определенным напряжением и силой достигает приемников. Исходя из построения получаем результат: UAB=UBC=UCA.

А это значит то, что если фазная система напряжений симметрична, то линейная система также симметрична и равна, а кроме того имеет сдвиг на 120 градусов. Это простое определение вектора трехфазной цепи.

Переменный ток представляет собой синусоиду, которая может быть графически наложена на ось координат. При этом вектор имеет угловую скорость вращения, которая равна угловым частотам тока. При построении необходимо также учесть то, что вектор является графическим изображением амплитуды колебания, в котором угол колебания равен начальной точке отсчета.

Например, за ось координаты выбрано значение 0. Также известно значение угла смещения. Далее стоит провести вектор «Im», который определяет направление движения тока. При построении вектора с использованием этих значений станут видны параметры опережения, отставания или сдвига фазы. Таким образом можно визуально увидеть разницу величин на каждом проводнике схемы.

Соединение фаз звездой

Рассмотрим схему соединения звездой

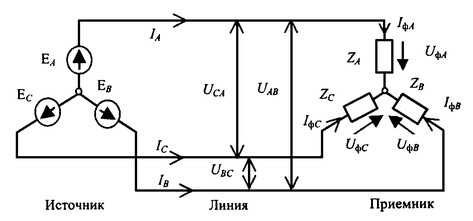
— фазные напряжения (напряжения между началом и концом соответствующей фазы);

— фазные токи — токи в фазах приемника;

— линейные напряжения (напряжения между началами двух соседних фаз);

— линейные токи — токи в линиях.

Для схемы соединения звездой очевидно равенство фазных и линейных токов. Независимо от характера нагрузки:

Из векторной диаграммы при равномерной (симметричной) нагрузке следует:

При неравномерной (несимметричной) нагрузке

Между точками 0 и 01 возникает напряжение несимметрии.

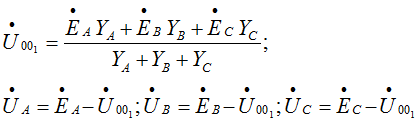
При симметричной нагрузке

При несимметричной нагрузке напряжения фаз приемника неодинаковы по величине и по фазе.

Для обеспечения симметричной системы напряжений во всех фазах и независимой работы отдельных приемников используется схема звезда с нулевым проводом или четырехпроводная система.

Поскольку узлы соединены нулевым проводом, напряжение между ними равно нулю. При несимметричной нагрузке фазные и линейные напряжения остаются постоянными.

Четырехпроводная система позволяет получать одновременно два напряжения — фазное и линейное, например, 220 и 380 В.

Для определения начала и конца обмотки поступают следующим образом. Начало одной из обмоток совершенно произвольно обозначают А, конец — X. Затем к ней присоединяют вторую обмотку, и если при этом напряжение увеличилось, значит, обмотки соединены концами, а начала свободны. Начало второй обмотки обозначают В, конец — Y. Таким же образом находят начало С и конец Z третьей обмотки.

Одним из существенных преимуществ четырехпроводной линии электропередачи и соединения обмоток генератора звездой является возможность получения в линии двух разных напряжений одновременно: фазных и линейных.

При строго симметричной нагрузке суммарный ток в общем проводе четырехпроводной линии равен нулю.

Таким образом, при симметричной нагрузке можно было бы обойтись без нулевого провода в линии, так как ток по нему не течет. Однако создать абсолютно симметричную нагрузку практически невозможно и ток обычно в нулевом проводе всегда есть, но он значительно меньше тока в фазах.

Преимущества использования четырехпроводной линии и роль при этом нулевого провода выясняются из следующего простого эксперимента. Соединим звездой три лампы накаливания Л1, Л2, Л3, а в нулевой и один из фазных проводов включим амперметры. Если все лампы совершенно одинаковы (симметричная нагрузка), то амперметр покажет отсутствие тока в нулевом проводе, а все лампы при его включении и отключении не изменят своего накала.

Теперь заменим лампу Л1 другой, например лампой меньшей мощности, т. е. создадим в цепи несимметричную нагрузку. Окажется, что без нулевого провода лампа Л1 горит с перекалом, а две другие — с недокалом. Если же нулевой провод включить, то все три лампы будут потреблять номинальный для них ток и светиться нормальным для каждой из них накалом, но зато в нулевом проводе потечет электрический ток. Однако, как показывает опыт, сила тока в нулевом проводе всегда меньше, чем в фазных проводах. Это позволяет уменьшить сечение нулевого провода по сравнению с фазными.

Таким образом, в четырехпроводной линии трехфазного тока силы токов через нагрузки, включенные звездой, при постоянных напряжениях регулируются автоматически, что создает благоприятные условия для работы электрических цепей при неизбежных на практике несимметричных нагрузках.

2.3 ВЕКТОРНЫЕ ДИАГРАММЫ

Для упрощения анализа и расчета цепей переменного тока целесообразно использовать векторы.

В электротехнике векторами изображаются изменяющиеся синусоидально ЭДС, напряжения и токи, но в отличие от векторов, которыми изображались силы и скорости в механике, эти векторы вращаются с постоянной угловой частотой ω и не означают направление действия.

Допустим, что радиус-вектор ОА (рис. 2.3,а), представляющий собой в определенном масштабе амплитудное значение ЭДС Ет , вращается с постоянной угловой частотой ω = 2πf против часовой стрелки. Проекция вектора ОА на вертикальную ось (ось у) будет равна

Оа = ОA sin α.

Выразив ОА через амплитудное значение ЭДС Ет и α через ωt, получим выражение мгновенного значения ЭДС, изменяющейся синусоидально:

е = Ет sin ωt.

График мгновенных значений ЭДС изображен на рис. 2.3,б. За начало отсчета выбран момент времени, когда радиус-вектор совпадает с горизонтальной осью (ось х).

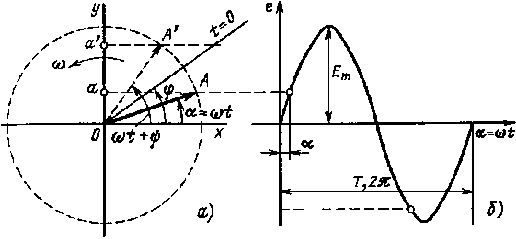Рис.  2.3.  Вращающиеся векторы (а) и график  мгновенных значений синусоидальной ЭДС (б)

Если в момент t = 0 радиус-вектор ОА совпадает с линией, расположенной под углом ψ к оси х, то проекция Оа’ и, следовательно, ЭДС будут соответственно равны

Оа’ = ОА’ sin (ωt + ψ),   е = Em sin (ωt + ψ).

Аналогично можно представить в виде векторов, вращающихся против часовой стрелки с постоянной угловой частотой ω, напряжение и ток.

Расчет цепей синусоидального тока производят в действующих значениях ЭДС, напряжений и токов. При этом суммирование Е, U, I проще осуществить с помощью вращающихся векторов, вместо того чтобы, сложив мгновенные значения е, и, i, определить действующие значения результирующих Е, U, I интегрированием гармонических функций. Адекватность этих действий можно обосновать так.

Допустим, что в каком-то узле цепи переменного тока (рис. 2.4, а) известны значения токов i1 и i2:

i1 = I1msin (ωt + ψ1);
i2 = I2msin (ωt + ψ2).

Требуется определить ток i.

На основании первого закона Кирхгофа мгновенное значение тока

i = i1 + i2,

i = I1msin (ωt + ψ1) + I2msin (ωt + ψ2).

Ток i можно определить аналитически путем тригонометрических преобразований  или графически сложением графиков мгновенных значений токов i1 и i2, как это сделано на рис. 2.4, б. Результирующий ток также изменяется синусоидально и в соответствии с рис. 2.4, б

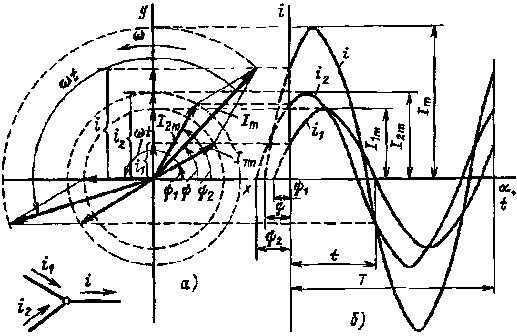Рис. 2.4. Сложение синусоидальных токов с помощью векторов (а): графики мгновенных значений токов (б)

i = Im sin (ωt + ψ).

Значительно проще произвести сложение токов i1 и i2, если изобразить амплитуды токов в виде векторов и сложить их по правилу параллелограмма. На рис. 2.4, а амплитуды токов I1m и I2m изображены в виде векторов под углами начальных фаз ψ1 и ψ2 относительно оси х. По прошествии времени t векторы повернутся на угол α = ωt. Проекции амплитуд на ось у составят

i1 = I1msin (ωt + ψ1);i2 = I2msin (ωt + ψ2).

Сложив векторы I1m и I2m по правилу параллелограмма (см. рис. 2,4, а), получим амплитуду результирующего тока Im . Сумма проекций токов I1m и I2m равна проекции результирующего тока Im :

i = i1 + i2.

Рис  2.5.  Векторная  диаграмма напряжений

Полученное выражение соответствует первому закону Кирхгофа  для  рассматриваемого узла  цепи   (см.   рис.   2.4, а). Из рис. 2.4. а видно, что взаимное расположение векторов I1m, I2m и Im в любой момент времени остается неизменным, так как они вращаются с постоянной угловой частотой ω. Аналогично можно определить сумму нескольких изменяющихся синусоидально с одинаковой частотой напряжений или ЭДС Например, в последовательной цепи переменного тока действуют три напряжения:

u1 = U1m sin (ωt + ψ1); u2 = U2msin (ωt + ψ2); u3 = U3msin (ωt + ψ3).
u = u1 + u2 + u3

Ūm = Ū1m + Ū2m + Ū3m

uUmt

Совокупность нескольких вращающихся векторов, соответствующих уравнениям электрической цепи, называется векторной диаграммой.

Обычно векторные диаграммы строят не для амплитудных, а для действующих значений. Векторы действующих значений отличаются от векторов амплитудных значений только масштабами, так как

I = Im /√2.

При построении векторных диаграмм обычно один из исходных векторов располагают на плоскости произвольно, остальные же векторы — под соответствующими углами к исходному. При этом в подавляющем большинстве случаев можно обойтись без нанесения осей координат х и у.

Несимметричные

Несимметричные цепи предполагают разницу сопротивлений на каждой фазе. Подобная разница может возникнуть при возникновении обрыва одного проводника или нейтрали, его плохого контакта, короткого замыкания. Например, при обрыве нейтрального провода возникает:

1. Увеличение сопротивления нейтрали.
2. Полное отсутствие проводимости.
3. Увеличение напряжения.
4. Максимальное искажение фазных напряжений.

При расчете несимметричной цепи также берется расчет соединения источника с приемниками по схеме звезда. Разница состоит в дополнительном расчете смещений, сдвигов фаз и величин сопротивления каждого проводника.

Ниже приведена векторная диаграмма несимметричной цепи.

Шпаргалки по электротехнике и электронике — Получение трехфазной системы ЭДС и способы представления

Sunday, 24 January 2016 04:20

administrator

Cмотрите так же…
Шпаргалки по электротехнике и электронике
Закон Ома для замкнутой цепи и для участка цепи
Законы Кирхгофа для цепи постоянного тока
Расчет простых цепей при различных схемах соединения потребителей
Понятие о сложной электрической цепи
Мощность, работа и потери КПД электрических цепей
Синусоидальный ток и его основные параметры
Способы представления синусоидального тока
Резисторное сопротивление в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Индуктивность в электрической цепи
Закон электромагнитной индукции
Индуктивность в цепи синусоидального тока
Взаимоиндуктивность в магнитосвязанных цепях
Законы Кирхгофа для цепей синусоидального тока
Закон Ома и сопротивления цепи синусоидального тока с последовательным соединением элементов R, L,C
Понятие о резонансе напряжений
Резонанс напряжений и его признаки
Закон Ома и проводимость цепи синусоидального тока с параллельным соединением ветвей R-L, L-C
Понятие о резонанс токов
Мгновенная мощь цепи синусоидального тока
Активная, реактивная и полная мощность цепей синусоидального тока
Коэффициент мощности и его экономическое значение
Получение трехфазной системы ЭДС и способы представления
Соединения обмоток трехфазных генераторов
Соединения приемников в трехфазных цепях
Мощность трехфазных цепей
Трансформаторы
Работа трансформаторов в различных режимах
Потери и КПД трансформаторов
Устройство, схемы и группы соединения обмоток трехфазных трансформаторов
Назначение, схема и работа автотрансформатора
Назначение, схема и работа импульсного трансформатора
Машины постоянного тока
Асинхронные электродвигатели
Синхронные электродвигатели
Пускорегулирующая аппаратура
Выбор типа и мощности электродвигателя
Провода и кабели, выбор сечения проводов
Защитное заземление
Электронно-дырочный переход
Диоды, тиристоры
Транзисторы
Основные логические операции и их реализация
Триггеры
Однофазные неуправляемые выпрямители
Трехфазные выпрямители: нулевой, мостовой
Фильтры(C, L, LC, RC), коэффициент пульсаций
Однофазные и трехфазные управляемые выпрямители
All Pages

Page 24 of 49

Получение трехфазной системы ЭДС и способы представления

Трехфазной системой электрических цепей называется система, состоящая из трех электрических цепей переменного тока одной частоты, ЭДС которых сдвинуты по фазе друг относительно друга на 1/3 периода.

Принцип получения трехфазной ЭДС может быть проиллюстрирован с помощью следующей простейшей модели: берутся три прямоугольные рамки, повернутые друг относительно друга на углы в 120 и жестко скрепленные между собой. Эти рамки приводятся во вращение с угловой частотой w в магнитном поле с постоянной индукцией В.

При этом в каждой из трех рамок будет наводиться переменная ЭДС. Пусть, например, в рамке А наводится ЭДС, которая изменяется по закону:

e_А = e_msinwt.

Но в рамке В тоже будет наводиться ЭДС, изменяющаяся также по синусоидальному закону; однако все процессы в рамке В будут запаздывать по отношению к процессам рамки А на угол в 120. Если в рамке А в некотором ее пространственном положении ЭДС принимает максимальное значение, то в рамке В в этот момент времени ЭДС не будет максимальна, а станет максимальной только тогда, когда рамка В займет то же положение, что и рамка А, т.е. когда повернется на угол 120. В рамке В закон изменения ЭДС имеет вид: e_В = e_msin(wt – 120). Аналогичным образом для рамки С: eС = e_msin(wt – 240) = e_msin(wt + 120).

Трехфазная симметричная система ЭДС может изображаться графиками, тригонометрическими функциями, векторами и функциями комплексного переменного.

Last Updated on Sunday, 24 January 2016 04:34

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂ (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

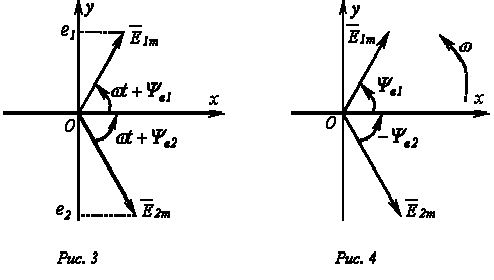
Пусть, например, в точке разветвления цепи (рис. 5) общий ток

Каждый из этих токов синусоидален и может быть представлен уравнением

Результирующий ток также будет синусоидален:

Определение амплитуды

t=0.w

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Построение векторной диаграммы в масштабе позволяет определить значения

«>

Однофазные электрические цепи переменного тока

Для получения, передачи и распределения электрической энергии применяются в основном устройства переменного тока: генераторы, трансформаторы, линии электропередачи и распределительные цепи переменного тока.

Постоянный ток, необходимый в некоторых областях народного хозяйства (транспорт, связь, электрохимия и др.), получают выпрямлением переменного тока.

Переменным электрическим током называют ток, периодически изменяющийся по величине и направлению.

Основное достоинство переменного тока заключается в возможности трансформировать напряжение. Кроме того, электрические машины переменного тока надежней в работе, проще по устройству и эксплуатации.

Говоря о переменном токе, обычно имеют в виду синусоидальный переменный ток, т. е. ток, изменяющийся по синусоидальному закону. При синусоидальном токе ЭДС электромагнитной индукции, самоиндукции и взаимоиндукции изменяются по синусоидальному закону.

Синусоидальный переменный ток проходит в замкнутой линейной электрической цепи под действием синусоидальной ЭДС.

Рассмотрим получение синусоидальной ЭДС. Если в однородном магнитном поле с индукцией В равномерно со скоростью V вращается рамка (рис. 10.1), то в каждой активной стороне этой рамки длиной

где а — угол, под которым активный проводник рамки пересекает магнитное поле (угол между

Плоскость называется нейтральной, т. к. ЭДС в рамке, расположенной в этой плоскости, равна нулю (а = 0, следовательно, sin а = 0).

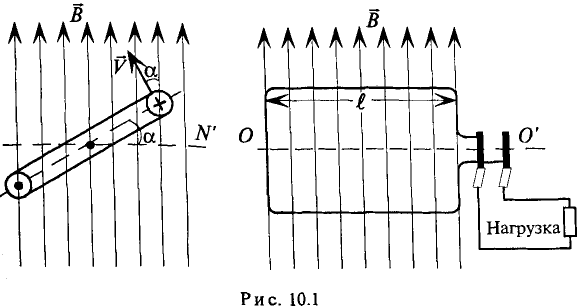
как — величина постоянная по условию, то е пропорциональна sin а, т. е. ЭДС в этой рамке, при вращении ее вокруг оси изменяется по синусоидальному закону. Если к этой рамке включить нагрузку (потребитель), то в замкнутой цепи (рис. 10.1) идет ток, который, как и ЭДС, изменяется по синусоидальному ну. Поэтому такой ток и называется синусоидальным.

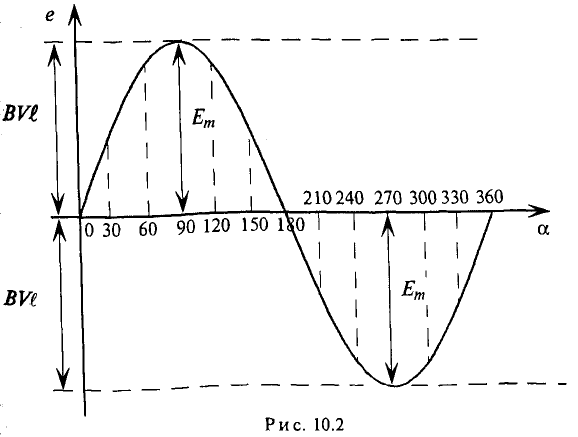
Синусоидальная ЭДС изображена на графике рис. 10.2. график принято называть «волновая диаграмма». (Если изменяющаяся величина изображена в зависимости от времени то ее называют «временная диаграмма».) На этой диаграмме синусоида ограничивает величины ЭДС (ординаты) при раз-личных углах поворота рамки относительно нейтральной плоскости NN». Как видно, синусоидальная ЭДС изменяется по величине и направлению.

Три фазы — основы

Трехфазная цепь — это совокупность трех электрических цепей, в которых действуют синусоидальные ЭДС, одинаковые по амплитуде и частоте, сдвинутые по фазе одна от другой на угол 120° (2π/3) и создаваемые общим источником энергии. Расшифруем это определение. В нем упоминаются следующие понятия:

• Общий источник энергии — это трехфазный генератор на электростанции, вырабатывающий напряжение порядка 10000 Вольт. Промежуточное звено между генератором и конечным потребителем — распределительный трансформатор, который условно можно заменить генератором 230 Вольт.
• Синусоидальные ЭДС сдвинутые по фазе одна от другой на угол 120°. Получение ЭДС (электродвижущей силы) основано на принципе электромагнитной индукции. При этом три фазы обмотки статора генератора повернуты в пространстве друг относительно друга на 1/3 часть окружности, то есть магнитные оси фаз повернуты в пространстве на угол 120°.
• Синусоидальные ЭДС, одинаковые по амплитуде и частоте. Если рассмотреть последний участок трансформации напряжения, то при привычном действующем напряжении 230 Вольт амплитуда каждой фазы 325 Вольт (230×√2). Частота ЭДС определяется частотой вращения ротора генератора. Частота 50 Гц значит, что ток пятьдесят раз в секунду идет в одну сторону и пятьдесят раз в обратную. При этом сто раз в секунду он достигает амплитудного значения и сто раз становится равным нулю. Смена направления происходит при переходе графика синусоиды через нулевое значение.

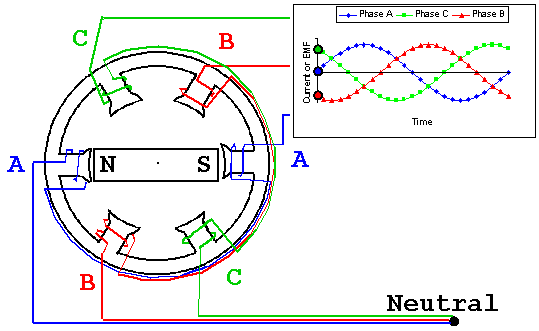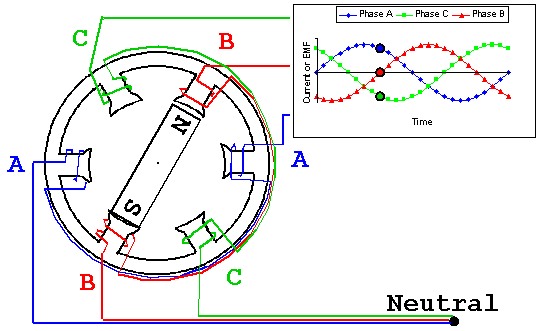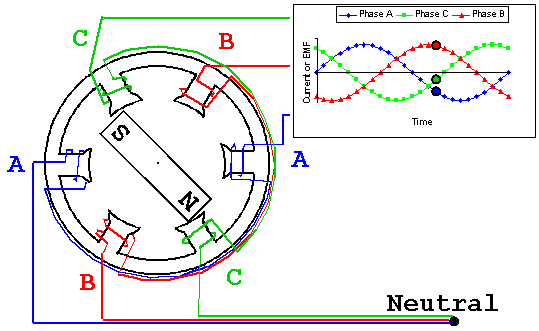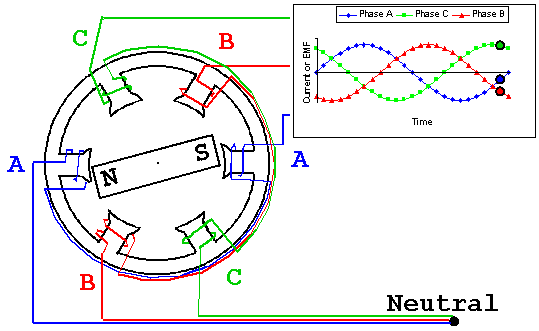
Термин «фаза» имеет в электротехнике два значения:

• Фазой называют аргумент синуса (ωt + Ψ). Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси). Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
• Каждая отдельная цепь, входящая в трехфазную цепь принято называть фазой.

Трехфазные цепи имеют широкое распространение за счет следующих преимуществ:

• Экономичности производства и передачи энергии по сравнению с однофазными цепями.
• Возможности простого получения кругового вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя.
• Возможности получения в одной установке двух эксплуатационных напряжений — фазного и линейного.

Основными элементами трехфазной цепи являются:

• Трехфазный генератор, преобразующий механическую энергию в электрическую.
• Трансформатор напряжения. Для передачи электроэнергии на большие расстояния напряжения электрического тока с помощью силовых трансформаторов повышают до сотен тысяч вольт. Конечные же потребители используют ток после силового понижающего трансформатора.
• Линии электропередач — один из компонентов электрической сети, система энергетического оборудования, предназначенная для передачи электроэнергии посредством электрического тока (токопроводы, кабельные и воздушные линии).
• Приемники (потребители), которые могут быть как трехфазными (например, трехфазные асинхронные двигатели), так и однофазными (например, лампы накаливания).

Каждая из трех фаз в цепи имеет стандартное наименование и цветовую маркировку:

• Первая фаза обозначается латинской буквой A и желтым цветом.
• Вторая фаза обозначается латинской буквой B и зеленым цветом.
• Третья фаза обозначается латинской буквой C и красным цветом.

Если идет речь о конкретном элементе цепи, например трехфазном генераторе, трансформаторе, то в данном случае фаза — это одна из трех обмоток генератора (трансформатора), имеющая начало и конец.
Начала обмоток фаз обозначаются латинскими буквами А, В, С, а
концы фаз — X, Y, Z.

3.1. Принципы построения трехфазной системы.

Три синусоидальные ЭДС одинаковой частоты и амплитуды, сдвинутые по
фазе на 120, образуют 3х-фазную симметричную систему.

1. 3х-фазная система позволяет получить вращающееся магнитное поле
с помощью 3х неподвижных катушек, что значительно упрощает электрические
двигатели.

2. 3х-фазная машина (генератор, двигатель, трансформатор) значительно
проще чем 3 однофазных.

3. Использование 3х-фазной системы позволяет получить 2 различных
напряжения (220/127 и т. д.).

4. При выпрямлении 3-х фазного напряжения пульсации минимальны.

3х-фазную ЭДС можно получить при вращении 3х рамок, взаимно расположенных
под углом 120 и находящихся в однородном магнитном поле
или при вращении магнитного поля при неподвижных рамках (обмотках).
ЭДС в обмотках:

E_А=Е_msinwt;

E_B=E_msin( wt
-120); 

E_C=E_msin(wt-240).

В действительности 3 обмотки размещены на статоре, а ротор, создающий
магнитное поле, вращается. Таким образом, для получения трехфазной ЭДС
используется синхронный генератор, соединенный проводами с 3х-фазным
потребителем (двигатель, трансформатор, лампа) образуя 3х-фазную цепь.
В 3х-фазной цепи протекает 3х-фазная система токов, т. е. синусоидальные
токи с тремя различными фазами. Участок цепи, по которому протекает
один из токов, называется фазой.

Возможны несколько способов соединения генератора с нагрузкой и наиболее
простым способом соединения является 3х-фазная несвязанная цепь (рис.
3.3), в которой каждая обмотка генератора питает свою нагрузку. Эта
цепь требует 6 проводов и практически не применяется.

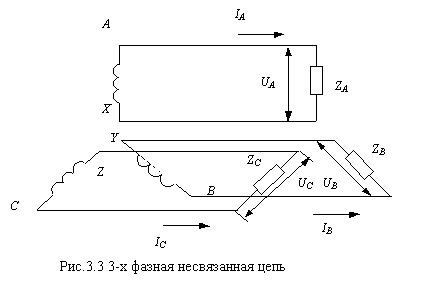
Начала обмоток – А,В и С, а концы – X , Y и Z

При симметричной нагрузке напряжения U_A, U_B,
U_С и токи I_A, I_B, J_C
– одинаковы.

Измерение мощности в трехфазной сети

Метод двух ваттметров для измерения мощности однородной трехфазной нагрузки представлен на рисунке. Для данной схемы независимо от соединения нагрузки можем записать:

По показаниям ваттметров при равномерной нагрузке можно определить угол нагрузки:

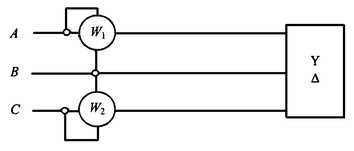
При симметричной нагрузке (модули и фазы сопротивлений нагрузки равны между собой) измерение мощности можно производить одним ваттметром, включенным на соответствующие фазное напряжение и фазный ток,

При несимметричной нагрузке требуется измерение тремя ваттметрами, включаемыми в каждую фазу.

Дополнительно по теме

• Понятие о многофазных источниках питания и о многофазных цепях
• Соединение звездой и многоугольником
• Симметричный режим трехфазной цепи
• Свойства трехфазных цепей
• Расчет симметричных режимов
• Расчет несимметричных режимов
• Напряжение на фазах приемника
• Эквивалентные схемы трехфазных линий
• Измерение мощности в 3-ф цепях
• Вращающееся магнитное поле
• Принцип действия асинхронного и синхронного двигателей

Значение нейтрального провода в трехфазной системе

При несимметричной нагрузке и отсутствии нейтрального провода фазные
напряжения приемника уже не связаны жестко с фазными напряжениями
генератора, так как на нагрузку воздействуют только линейные напряжения
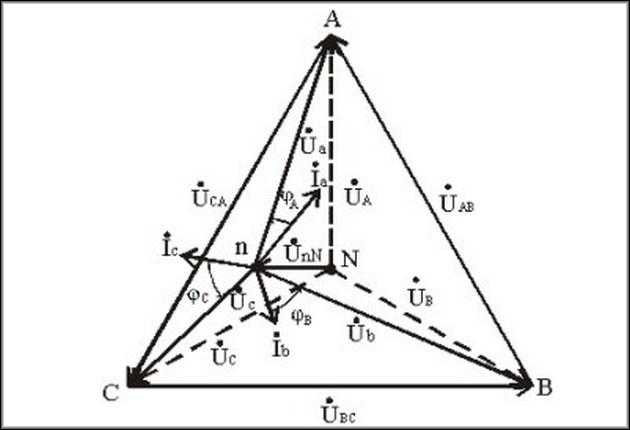
генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений (UA, UB, UC) и смещение ее нейтральной точки () из центра треугольника напряжений (смещение нейтрали).

Естественно треугольник напряжений (векторы фазных напряжений) и сложные формулы расчетов мы рассматривать не будем. Постараемся, как и в предыдущих пунктах, разобраться с вопросом наглядно и упрощенно:

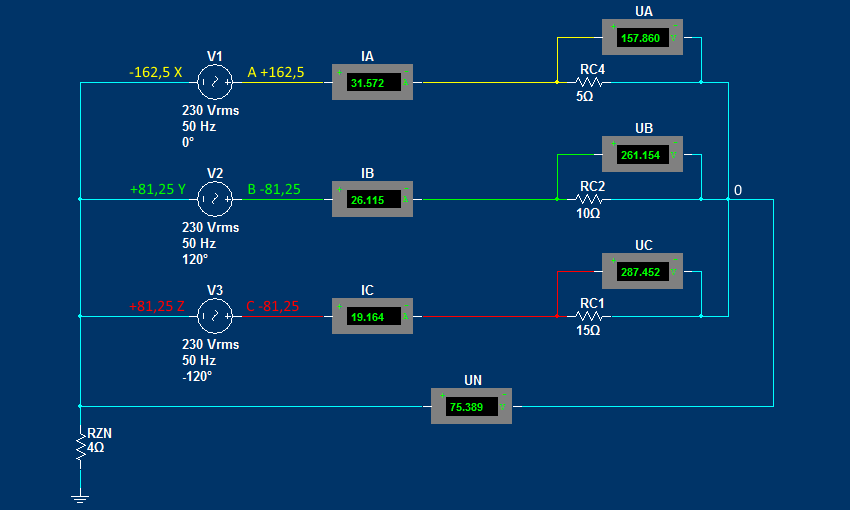
В приведенной выше схеме наблюдается несимметрия потребления. Фаза A нагружена больше и имеет сопротивление 5 Ом. Фаза B нагружена меньше и имеет сопротивление 10 Ом. Фаза C нагружена еще меньше и имеет сопротивление 15 Ом. С учетом этого произошла несимметрии фазных напряжений (UA ≈ 157 Вольт, UB ≈ 261 Вольт, UC ≈ 287 Вольт). Смещение нейтральной точки соединения приемников () привело к появлению разности потенциалов с нейтралью трансформатора UN = 75 Вольт.

Перейдем к потенциалам на выводах генератора (трансформатора). Они остались такими же, как и при симметричной нагрузке приемников

В конце предыдущего пункта мы отметили важность сбалансированности и одинаковой скорости движения электронов в цепи (для справки: ток у нас не постоянный, потому движение условное, и фактически — это «топтание на месте»). Как же происходит движение зарядов в данном случае, когда изменились параметры «путепроводов» (различное сопротивление на участках цепи):

• Определенное количество зарядов (x) со скоростью (v) проходит по фазному проводу А, проходит нагрузку R = 5 Ом и попадает в точку соединение трех несимметричных нагрузок (приемников).
• Из общей точки заряды уже не разделяются пополам. Виной тому увеличение сопротивления на пути от нейтральной точки приемников к выводам фаз B и C на трансформаторе. Баланс нарушился, и теперь то количество зарядов, пришедших от вывода A попросту не успевают перераспределится в цепи. Образуется избыток в данный момент времени зарядов в точке соединения нагрузок (0). Раз есть избыток (или недостаток в определенный момент периода синусоиды) в этой нулевой точке, то есть и разность потенциалов с нейтралью трансформатора (что и показал вольтметр UN).

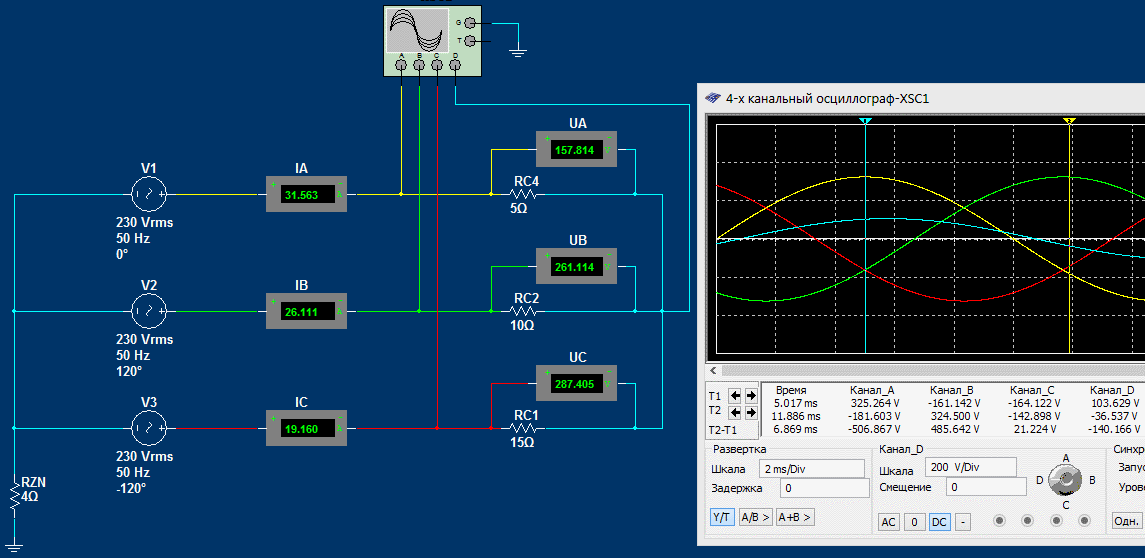
Так как в нейтральной точке имеется потенциал, отличный от нуля, то это приводит к несимметрии фазных напряжений. К примеру, если бы потенциал в нейтральной точке был равен 0 Вольт (случай симметричной нагрузки), то фазное напряжение UA можно было бы рассчитать, как +162,5-(-162,5)-0 = 325 Вольт (амплитудное значение). 325/√2 ≈ 230 Вольт (действующее значение). В случае с несимметричным потреблением в нейтральной точке будет всегда какой-то потенциал. Соответственно при расчетах мы получим иное амплитудное и действующее значение напряжения. Из примера просчитанного в программе видно, что действующее напряжение UA ≈ 157 Вольт. Соответственно амплитудное равно 157×√2 ≈ 222 Вольт. Это можно наглядно увидеть на графиках синусоид, приведенных выше. Берем пик синусоиды фазы A с напряжением (потенциалом) +325 Вольт, и от этого потенциала отнимаем потенциал нейтрали (канал D) +103 Вольт в данный момент времени. То же самое можно сделать с остальными фазами. Берем пик синусоиды фазы B с напряжением (потенциалом) +325 Вольт, и от этого потенциала отнимаем потенциал нейтрали (канал D) -36 Вольт в данный момент времени. Получаем +325-(-36) = +361 Вольт (амплитудное значение). 355×√2 ≈ 255 Вольт (действующее значение). Приблизительно это и показывает вольтметр UB ≈ 261 Вольт.

Для того чтобы выравнивать фазные напряжения приемника при несимметричной нагрузке, нужен нейтральный провод соединяющий нулевые точки трансформатора (генератора) и приемников:

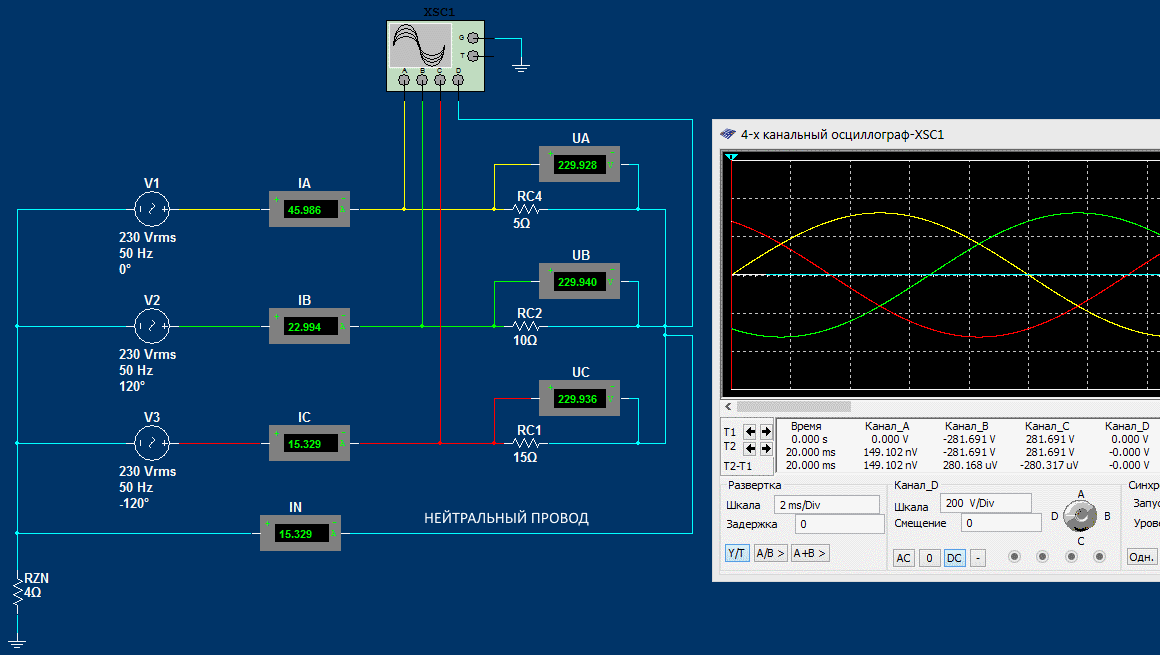
При наличии нейтрального провода в общей точке соединения нагрузок уже не может образовываться излишек или недостаток зарядов (потенциал), так как он сразу же будет перенаправляется в общую точку соединения концов фазных обмоток трансформатора (генератора).

Завершая тему трех фаз с нулем и без нуля стоит также отметить, что наличие нейтрального провода в цепи при несимметричной нагрузке, также позволяет подключать однофазные приемники с номинальным напряжением в √3 раз меньше номинального линейного напряжения трехфазной сети (230/400 Вольт).