Закон сохранения электрического заряда

Закон Кулона

Закон Кулона был открыт экспериментально: в опытах с использованием крутильных весов измерялись силы взаимодействия заряженных шаров.

Закон Кулона формулируется так:
сила взаимодействия ​\( F \)​ двух точечных неподвижных электрических зарядов в вакууме прямо пропорциональна их модулям ​\( q_1 \)​ и \( q_2 \) и обратно пропорциональна квадрату расстояния между ними ​\( r \)​:

где ​\( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \)​ (Н·м2)/Кл2 – коэффициент пропорциональности,
​\( \varepsilon_0=8.85\cdot10^{-12} \)​ Кл2/(Н·м2) – электрическая постоянная.

Коэффициент ​\( k \)​ численно равен силе, с которой два точечных заряда величиной 1 Кл каждый взаимодействуют в вакууме на расстоянии 1 м.

Сила Кулона направлена вдоль прямой, соединяющей взаимодействующие заряды. Заряды взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению.

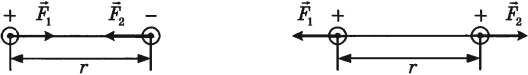
Значение силы Кулона зависит от среды, в которой они находятся. В этом случае формула закона:

где ​\( \varepsilon \)​ – диэлектрическая проницаемость среды.

Закон Кулона применим к взаимодействию

• неподвижных точечных зарядов;
• равномерно заряженных тел сферической формы.

В этом случае ​\( r \)​ – расстояние между центрами сферических поверхностей.

Важно!
Если заряженное тело протяженное, то его необходимо разбить на точечные заряды, рассчитать силы их попарного взаимодействия и найти равнодействующую этих сил (принцип суперпозиции)

Основные законы движения заряженных частиц в электрическом поле

Движение заряженных частиц в электрическом поле определяется несколькими основными законами электродинамики. Вот некоторые из них:

1. Закон Кулона: взаимодействие между двумя заряженными частицами пропорционально произведению их зарядов и обратно пропорционально квадрату расстояния между ними. Формула для силы взаимодействия: F = k * (q1 * q2) / r^2, где F — сила взаимодействия, q1 и q2 — заряды частиц, r — расстояние между ними, k — постоянная пропорциональности.

2. Закон Ньютона: движение заряженных частиц в электрическом поле описывается вторым законом Ньютона: сумма всех сил, действующих на частицу, равна произведению ее массы на ускорение. Формула: F = m * a, где F — сумма сил, m — масса частицы, a — ускорение.

3. Закон Лоренца: сила, действующая на заряженную частицу в электрическом и магнитном полях, описывается законом Лоренца: F = q * (E + v * B), где F — сила, q — заряд частицы, E — напряженность электрического поля, v — скорость частицы, B — индукция магнитного поля.

4. Уравнение движения: для определения траектории движения заряженной частицы в электрическом поле используется уравнение движения. Для простого электрического поля с однородной напряженностью E и отсутствием магнитного поля, уравнение движения имеет вид: m * a = q * E, где m — масса частицы, a — ускорение, q — заряд частицы, E — напряженность электрического поля.

Эти законы позволяют определить траекторию движения заряженной частицы в электрическом поле и установить зависимость этой траектории от массы, заряда и величины полей

Важно также учитывать наличие других сил и факторов, таких как сопротивление среды, магнитное поле и другие, которые могут влиять на движение частицы

Потенциальность электростатического поля

Электрическое поле с напряженностью ​\( \vec{E} \)​ при перемещении заряда ​\( q \)​ совершает работу. Работа ​\( A \)​ электростатического поля вычисляется по формуле:

где ​\( d \)​ – расстояние, на которое перемещается заряд,
​\( \alpha \)​ – угол между векторами напряженности электрического поля и перемещения заряда.

Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле. Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.

Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.

Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным

Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой ​\( W \)​, так как буквой ​\( E \)​ обозначают напряженность поля:

Потенциальная энергия заряда ​\( q \)​, помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.

Напряженность электрического поля

Напряженность электрического поля ​\( \vec{E} \)​ – векторная физическая величина, равная отношению силы ​\( F \)​, действующей на пробный точечный заряд, к величине этого заряда ​\( q \)​:

Обозначение – \( \vec{E} \), единица измерения в СИ – Н/Кл или В/м.

Напряженность поля точечного заряда в вакууме вычисляется по формуле:

где \( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \) (Н·м2)/Кл2,
​\( q_0 \)​ – заряд, создающий поле,
​\( r \)​ – расстояние от заряда, создающего поле, до данной точки.

Напряженность поля точечного заряда в среде вычисляется по формуле:

где ​\( \varepsilon \)​ – диэлектрическая проницаемость среды.

Важно!
Напряженность электрического поля не зависит от величины пробного заряда, она определяется величиной заряда, создающего поле. Направление вектора напряженности в данной точке совпадает с направлением силы, с которой поле действует на положительный пробный заряд, помещенный в эту точку

Направление вектора напряженности в данной точке совпадает с направлением силы, с которой поле действует на положительный пробный заряд, помещенный в эту точку.

Линией напряженности электрического поля называется линия, касательная к которой в каждой точке направлена вдоль вектора напряженности ​\( \vec{E} \)​.

Линии напряженности электростатического поля начинаются на положительных электрических зарядах и заканчиваются на отрицательных электрических зарядах или уходят в бесконечность от положительного заряда и приходят из бесконечности к отрицательному заряду.

Распределение линий напряженности вокруг положительного и отрицательного точечных зарядов показано на рисунке.

Определяя направление вектора ​\( \vec{E} \)​ в различных точках пространства, можно представить картину распределения линий напряженности электрического поля.

Поле, в котором напряженность одинакова по модулю и направлению в любой точке, называется однородным электрическим полем. Однородным можно считать электрическое поле между двумя разноименно заряженными металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу.

Движение заряженной частицы в магнитном поле.

Для вывода общих закономерностей движения заряженной частицы в магнитном поле будем считать магнитное поле однородным, электрические поля на частицу не действуют. При этом учтем очевидное:

а) Если заряженная частица движется в магнитном поле вдоль силовой линии, сила Лоренца, действующая на неё, равна нулю

б) Если заряженная частица движется в магнитном поле со скоростью , перпендикулярно к вектору , то сила Лоренца, равная постоянна по модулю и перпендикулярна к траектории частицы.

Согласно второму закону Ньютона, эта сила создаёт центростремительное ускорение. Поэтому частица будет двигаться по окружности, радиус которой определяется из условия:

, , ,

период вращения частицы, т. е. время, затрачиваемое ею на один полный оборот,

в) Если скорость заряженной частицы направлена под углом к вектору то её движение можно представить в виде двух движений: 1) равномерного прямолинейного движения вдоль поля, 2) равномерного движения по окружности в плоскости перпендикулярной полю (Рис. 23).

В результате этих двух движений возникает движение по винтовой линии, ось которой параллельна вектору . Шаг винтовой линии:

Направление, в котором закручивается частица, зависит от знака её заряда.

Действие магнитного поля на движущиеся заряженные частицы. Действие магнитного поля на проводник с током означает, что магнитное поле действует на движущиеся электрические заряды. Найдем силу, действующую на электрический заряд q при его движении в однородном магнитном поле с индукцией . Сила тока I в проводнике связана с концентрацией n свободных заряженных частиц, скоростью их упорядоченного движения и площадью S поперечного сечения проводника следующим выражением:

,(1)

где q — заряд отдельной частицы.

.

Так как произведение nSl равно числу свободных заряженных частиц в проводнике длиной l

то сила, действующая со стороны магнитного поля на одну заряженную частицу, движущуюся со скоростью под углом к вектору индукции, равна

.(2)

Эту силу называют силой Лоренца. Направление вектора силы Лоренца определяется правилом левой руки, в нем за направление тока нужно брать направление вектора скорости положительного заряда (рис. 186). Для случая движения отрицательно заряженных частиц четыре пальца следует располагать противоположно направлению вектора скорости.

Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила , постоянная по модулю и направленная перпендикулярно вектору скорости (рис. 187).

В вакууме под действием силы Лоренца частица приобретает центростремительное ускорение

(3)

и движется по окружности. Радиус r окружности, по которой движется частица, определяется из условия

, .(4)

Период обращения частицы в однородном магнитном поле равен

.(5)

Последнее выражение показывает, что период обращения частицы в однородном магнитном поле при постоянной массе не зависит от скорости и радиуса r траектории ее движения. Этот факт используется, например, в ускорителе заряженных частиц — циклотроне.

Циклотрон. В этом ускорителе заряженные частицы — протоны, ядра атомов гелия — разгоняются переменным электрическим полем постоянной частоты в вакууме в зазоре между двумя металлическими электродами — дуантами. Дуанты находятся между полюсами постоянного электромагнита (рис. 188, а).

Под действием магнитного поля внутри дуантов заряженные частицы движутся по окружности. К моменту времени, когда они совершают половину оборота и подходят к зазору между дуантами, направление вектора напряженности электрического поля между дуантами изменяется на противоположное и частицы вновь испытывают ускорение. Каждую следующую половину оборота частицы пролетают по окружности все большего радиуса (рис. 188, б), но период их обращения остается неизменным. Поэтому для ускорения частиц на дуанты подается переменное напряжение с постоянным периодом. Ускорение частиц в циклотроне с постоянным периодом возможно лишь до значений скоростей, значительно меньших скорости света. С приближением скорости частицы к скорости света в вакууме, равной c = 300000 км/с, масса частицы возрастает, вследствие чего увеличивается период ее обращения в магнитном поле. Равенство периода обращения частицы и периода изменения электрического поля нарушается, ускорение прекращается.

топлива по сравнению с обычной тепловой электростанцией.

В заключение, по традиции, предлагаем Вашему вниманию шпаргалку по этой теме:

ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКОМ И МАГНИТНОМ ПОЛЯХ. СИЛА ЛОРЕНЦА

Электрическое и магнитное поля действуют на движущиеся заряды, в результате чего заряженная частица, попадая в поле, меняет свою траекторию. Исключение составляет тот случай, когда направление движения заряда совпадает с направлением поля и при этом в электрическом поле происходит ускорение или замедление его. А магнитное поле в данном случае вообще не взаимодействует с зарядом.

Пусть электрон влетает по горизонтали со скоростью v в электрическое поле с напряженностью Ё плоского конденсатора длиной х. Под действием силы поля Ё_эл = еЁ = та электрон смещается полем вверх, двигается по криволинейной траектории и вылетает из конденсатора, отклонившись от первоначального направления на отрезок у, как показано на рис. 12.8. Движение того же электрона в однородном магнитном поле (рис. 12.9), представляет собой электрический ток. Поэтому магнитное поле отклонит частицу вверх от первоначальной траектории. Согласно закону Ампера сила, отклоняющая электрон на любом участке / траектории, равна f_A = IBlsina. Но так как сила тока / = е /1, где t — время, за которое заряд е проходит участок /, то F_{a = eB(l / /)sina. Учитывая, что / /1 = и и в общем случае е =q, получим}

Силу F_n называют силой Лоренца. Направления векторов F_n,vn В взаимно перпендикулярны. Направление силы Лоренца, действующей на положительный заряд, можно определить по правилу левой руки, как и направление силы Ампера, с той лишь разницей, что четыре вытянутых пальца следует направить вдоль вектора v.

При этом нельзя забывать, что для положительного заряда направления I и v совпадают, а для отрицательного — противопо-

ложны. Так как сила Лоренца перпендикулярна вектору скорости, то она изменяет только направление скорости движения заряда, не изменяя модуля этой скорости. Это значит, что работа силы Лоренца равна нулю.

Иными словами, постоянное магнитное поле не совершает работы над движущимся с постоянной скоростью зарядом. Вспомним, что электрическое поле изменяет энергию и модуль скорости движущегося заряда.

Из формулы (12.7) очевидно, что направление силы Лоренца и направление вызываемого ею отклонения заряда зависят от взаимного направления векторов у и В. Возможны следующие варианты соотношения направлений векторов у и В.

Первый: у || В, а = vB = 0°, sina = 0, F_n= 0 — это значит, что магнитное поле на заряд не действует.

Действие электрического поля на электрические заряды

Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.

Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.

Свойства электрического поля заключаются в том, что оно:

• материально;
• создается зарядом;
• обнаруживается по действию на заряд;
• непрерывно распределено в пространстве;
• ослабевает с увеличением расстояния от заряда.

Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.

Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:

где ​\( \vec{E} \)​ – напряженность электрического поля, ​\( q \)​ – заряд.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.

Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:

• сделать рисунок; указать силы, действующие на точечный заряд, помещенный в электрическое поле;
• записать для заряда условие равновесия или основное уравнение динамики материальной точки;
• выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение;
• если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавить уравнение закона сохранения зарядов;
• записать математически все вспомогательные условия;
• решить полученную систему уравнений относительно неизвестной величины;
• проверить решение

Влияние электрического поля на траекторию движения заряженных частиц

Электрическое поле оказывает значительное влияние на траекторию движения заряженных частиц. Заряженная частица, находящаяся в электрическом поле, испытывает силу, называемую электрической силой. Эта сила влияет на движение частицы и определяет ее траекторию.

Основным законом, описывающим движение заряженной частицы в электрическом поле, является закон Кулона. Согласно этому закону, электрическая сила между двумя заряженными частицами пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между ними. Таким образом, если одна из заряженных частиц является фиксированной, то траектория движения другой частицы будет представлять собой кривую линию.

Траектория движения заряженной частицы в электрическом поле может принимать различные формы в зависимости от силы и направления электрической силы. Например, если электрическая сила равна нулю, то частица движется по прямой линии с постоянной скоростью.

Если электрическое поле равномерное, то траектория частицы будет представлять собой прямую линию, перпендикулярную линиям электрического поля. Если электрическое поле неоднородное, то траектория частицы будет изгибаться.

• Если заряженная частица движется параллельно линиям электрического поля, то ее траектория будет являться прямой линией.
• Если заряженная частица движется перпендикулярно линиям электрического поля, то ее траектория будет являться окружностью или дугой.
• Если заряженная частица движется под углом к линиям электрического поля, то ее траектория будет являться спиралью.

Важно отметить, что заряженные частицы, такие как электроны и протоны, могут существовать только в определенных энергетических состояниях, называемых орбитами или энергетическими уровнями. Принцип неопределенности Гейзенберга указывает на то, что точное понятие о траектории заряженных частиц в электрическом поле невозможно, так как измерение их положения и скорости одновременно является невозможным

Таким образом, электрическое поле играет важную роль в определении траектории движения заряженных частиц. Закон Кулона и другие физические законы позволяют описать и предсказать траекторию движения заряженных частиц в различных условиях электрического поля.

Энергия электрического поля конденсатора

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Электрическая энергия конденсатора сосредоточена в пространстве между обкладками конденсатора, то есть в электрическом поле, поэтому ее называют энергией электрического поля. Формулы для вычисления энергии электрического поля:

Так как напряженность электрического поля прямо пропорциональна напряжению, то энергия электрического поля конденсатора пропорциональна квадрату напряженности.

Плотность энергии электрического поля:

где ​\( V \)​ – объем пространства между обкладками конденсатора.

Плотность энергии не зависит от параметров конденсатора, а определяется только напряженностью электрического поля.

Примеры траекторий движения заряженных частиц в электрическом поле

Физика заряженных частиц и их движение в электрическом поле имеет множество применений и примеров. Ниже приведены некоторые наиболее распространенные примеры траекторий заряженных частиц:

• Прямолинейное движение: Если заряженная частица движется под воздействием постоянного электрического поля, то ее траектория будет прямолинейной. Например, электрон в вакууме между двумя электродами.
• Круговое движение: Когда заряженная частица движется вокруг центра под воздействием электрического поля, ее траектория будет круговой. Примером может быть электрон, движущийся вокруг ядра атома.
• Спиральное движение: В некоторых случаях заряженная частица может двигаться по спиральной траектории. Это происходит при одновременном воздействии электрического и магнитного полей. Примером может быть электрон в магнитном поле, которое перпендикулярно электрическому полю.
• Параболическое движение: Если заряженная частица имеет начальную скорость под определенным углом к электрическому полю, ее траектория будет параболической. Это происходит при сочетании электрического поля и свободного падения. Примером может быть электрон, вылетающий из катода и движущийся в электрическом поле вблизи анода.

Эти примеры являются лишь некоторыми из множества возможных траекторий заряженных частиц в электрическом поле. В каждом конкретном случае форма и свойства траектории определяются массой и зарядом частицы, напряжением и ориентацией электрического поля, а также наличием других внешних воздействий, таких как магнитное поле.

Изучение этих траекторий позволяет углубить понимание движения заряженных частиц и применить полученные знания в таких областях, как физика элементарных частиц, электроника и спектроскопия.

Электрическая емкость. Конденсатор

Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.

Обозначение – ​\( C \)​, единица измерения в СИ – фарад (Ф).

Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.

Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:

Формула для вычисления электроемкости:

где ​\( q \)​ – заряд проводника, ​\( \varphi \)​ – его потенциал.

Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.

Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.

Электроемкость конденсатора рассчитывается по формуле:

где ​\( q \)​ – модуль заряда одной из обкладок,
​\( U \)​ – разность потенциалов между обкладками.

Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.

Плоский конденсатор представляет две параллельные пластины площадью ​\( S \)​, находящиеся на расстоянии ​\( d \)​ друг от друга.

Электроемкость плоского конденсатора:

где ​\( \varepsilon \)​ – диэлектрическая проницаемость вещества между обкладками,\( \varepsilon_0 \) – электрическая постоянная.

На электрической схеме конденсатор обозначается:

Виды конденсаторов:

• по типу диэлектрика – воздушный, бумажный и т. д.;
• по форме – плоский, цилиндрический, сферический;
• по электроемкости – постоянной и переменной емкости.

Конденсаторы можно соединять между собой.

Параллельное соединение конденсаторов

При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:

Общая емкость:

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.

Заряды конденсаторов при таком соединении равны:

Общее напряжение:

Величина, обратная общей емкости:

При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.

Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости

Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.

Движение заряженных частиц в электрических и магнитных полях

Содержание работы

Движение заряженных частиц в электрических и магнитных полях

Неквантовомеханическое описание движения заряженных частиц в заданных электромагнитных полях осуществляется на языке систем обыкновенных дифференциальных уравнений. Исчерпывающи математический алгоритм решения таких систем существует лишь в случае, когда входящие в них уравнения являются линейными и имеют постоянные коэффициенты. Этому соответствует нерелятивистское движение частиц в пространственно однородных электрических и постоянных во времени магнитных полях.

11.1. Уравнение движения

В случаях, когда квантовомеханические эффекты несущественны, описание движения заряженных частиц в электромагнитных полях может строиться на базе второго закона Ньютона в импульсной формулировке (11.1), применимого не только в классическом приближении, но и в релятивистском случае. В качестве сил, действующих на частицу следует рассматривать электрические, магнитные и диссипативные силы, вводимые для описания потерь механической энергии движущимся зарядом (11.2). Последние обычно считаются пропорциональными скорости движения частиц (аналогичная зависимость возникает при медленном движении тел в вязкой жидкости). В случае движения заряженных частиц в электромагнитных полях выбор линейной зависимости от скорости величины диссипативной скорости силы обусловлен двумя причинами. Первая состоит в том , что с токи зрения решения дифференциальных уравнений наличие в них линейных слагаемых всегда предпочтительно. Вторая причина имеет более глубоких физический смысл: потери механической энергии частицами, движущимися с ускорением, обусловлены излучением ими электромагнитных волн. Приближенное выражение для соответствующей силы радиационного трения может быть получено в рамках последовательной релятивистской теории и оказывается пропорциональным производной по времени от ускорения (11.3.). В часто встречающихся на практике случаях гармонических колебаниях и при движении по окружности (последнее сводится к двум взаимно перпендикулярным гармоническим колебаниям) вторая производная от скорости оказывается пропорциональной самой скорости, что в некоторой степени и оправдывает сделанный выбор для зависимости диссипативной силы.(11.4).

Следует иметь ввиду, что эффект радиационного трения имеет релятивистскую природу, что часто приводит к противоречиям при попытках его классического толкования. Например, возникает проблема выбора второго тела, взаимодействие с которым приводит к возникновению сил радиационного трения. Другим примером возникающих трудностей является получающийся при подстановке одной только силы радиационного трения в классическое уравнение движения явно абсурдный результат, соответствующий саморазгону заряженной частицы в пустом пространстве. Последний означает, что учет этой силы оправдан только в тех случаях, когда она проявляется на фоне других, более эффективных сил.

В приближении малых скоростей уравнение движения заряда в постоянном магнитном и пространственно однородном электрическом поле при наличии сил вязкого трения с точки зрения математики представляет собой систему обыкновенных линейных дифференциальных уравнений первого порядка относительно декартовых компонент вектора скорости. Поскольку подобные системы уравнений весьма часто встречаются в физике, представляется целесообразным на частных примерах движения частиц в электромагнитных полях познакомиться с общими методами их решения. При решении уравнения движения полезно иметь ввиду теорему существования и единственности решения обыкновенного дифференциального уравнения порядка N, для которого поставлено N начальных условий.

Релятивистское уравнение движения частицы в силовом поле (аналог второго закона Ньютона).

Силы, действующие на заряженную частицу, движущуюся в электромагнитном поле.

4 вариант

A1. Прямолинейный проводник длины l с током I помещён в однородное магнитное поле, направление линий индук­ции которого противоположно направлению тока. Если силу тока уменьшить в 2 раза, а индукцию магнитного поля увеличить в 4 раза, то действующая на проводник сила Ампера

1) увеличится в 2 раза
2) не изменится
3) уменьшится в 4 раза
4) уменьшится в 2 раза

А2. Участок проводника длиной 10 см находится в магнитном поле индукцией 50 мТл. Сила электрического тока, протекающего по проводнику, 5 А. Проводник расположен перпендикулярно линиям магнитной индукции. Какую работу совершает сила Ампера при перемещении проводника на 80 см в направлении своего действия?

1) 0,004 Дж
2) 0,4 Дж
3) 0,5 Дж
4) 0,625 Дж

А3. Электрон е—, влетевший в зазор между полюсами электромагнита, имеет горизонтальную скорость v, перпендикулярную вектору индукции В магнитного поля (см. рис.). Куда направлена действующая на него сила Лоренца F?

1) К нам из-за плоскости рисунка
2) От нас перпендикулярно плоскости рисунка
3) Горизонтально влево в плоскости рисунка
4) Горизонтально вправо в плоскости рисунка

А4. При движении проводника в однородном магнитном поле в проводнике возникает ЭДС индукции E₁. При уменьшении скорости движения проводника в 2 раза ЭДС ин­дукции E₂ будет равна

1) 2E₁
2) E₁
3) 0,5E₁
4) 0,25E₁

А5. На железный сердечник надеты две катушки. К первой подключён амперметр, ток во второй меняется согласно приведённому графику. В какие промежутки времени амперметр покажет наличие тока в первой катушке?

1) 0-1 с и 2-4 с
2) 0-1 с и 4-7 с
3) 1-2 с и 4-7 с
4) 1-2 с и 3-4 с

B1. Электрон, обладающий зарядом е = 1,6 · 10-19 Кл, дви­жется в однородном магнитном поле индукцией В по круговой орбите радиусом R = 6 · 10-4 м. Значение импульса частицы равно р = 4,8 · 10-24 кг· м/с. Чему равна индукция В магнитного поля?

В2. Частица массой m, несущая заряд q, движется в одно­родном магнитном поле индукцией В по окружности ра­диуса R со скоростью v. Что произойдёт с радиусом ор­биты, периодом обращения и импульсом частицы при уменьшении индукции магнитного поля?

К каждой позиции первого столбца подберите соответст­вующую позицию второго.

Физические величины

А) радиус орбиты
Б) период обращения
В) импульс частицы

Их изменения

1) увеличится
2) уменьшится
3) не изменится

C1. Из точечного источника вылетают α-частицы массой m и зарядом q и движутся в однородном магнитном поле с индукцией В, силовые линии которого перпендикулярны плоскости рисунка. На расстоянии L от источника нахо­дится мишень радиуса r. При каких значениях скорости α-частицы попадут на поверхность мишени?

Взаимодействие зарядов. Два вида зарядов

Электрический заряд – скалярная физическая величина, характеризующая способность тела участвовать в электромагнитных взаимодействиях.

Обозначение – ​\( q \)​, единица измерения в СИ – кулон (Кл).

Существуют два вида электрических зарядов: положительный и отрицательный. Наименьший отрицательный заряд имеет электрон (–1,6·10-19 Кл), наименьший положительный заряд (1,6·10-19 Кл) – протон. Минимальный заряд, который может быть сообщен телу, равен заряду электрона (элементарный заряд). Если тело имеет избыточные (лишние) электроны, то тело заряжено отрицательно, если у тела недостаток электронов, то тело заряжено положительно.

Величина заряда тела будет равна

где ​\( N \)​ — число избыточных или недостающих электронов;
​\( e \)​ — элементарный заряд, равный 1,6·10-19 Кл.

Важно!
Частица может не иметь заряда, но заряд без частицы не существует. Электрические заряды взаимодействуют:

Электрические заряды взаимодействуют:

заряды одного знака отталкиваются:

заряды противоположных знаков притягиваются:

Прибор для обнаружения электрического заряда называется электроскоп. Основная часть прибора – металлический стержень, на котором закреплены два листочка металлической фольги, помещенные в стеклянный сосуд. При соприкосновении заряженного тела со стержнем электроскопа заряды распределяются между листочками фольги. Так как заряд листочков одинаков по знаку, они отталкиваются.

Для измерения зарядов можно использовать и электрометр. Основные части его – металлический стержень и стрелка, которая может вращаться вокруг горизонтальной оси. Стержень со стрелкой закреплен в пластмассовой втулке и помещен в металлический корпус, закрытый стеклянными крышками. При соприкосновении заряженного тела со стержнем стержень и стрелка получают электрические заряды одного знака. Стрелка поворачивается на некоторый угол.