Основные этапы компьютерного моделирования

Процесс управления с помощью модели

Процесс управления объектом с помощью модели можно рассматривать как процесс управления знанием или обучения модели (рис. 1.1).

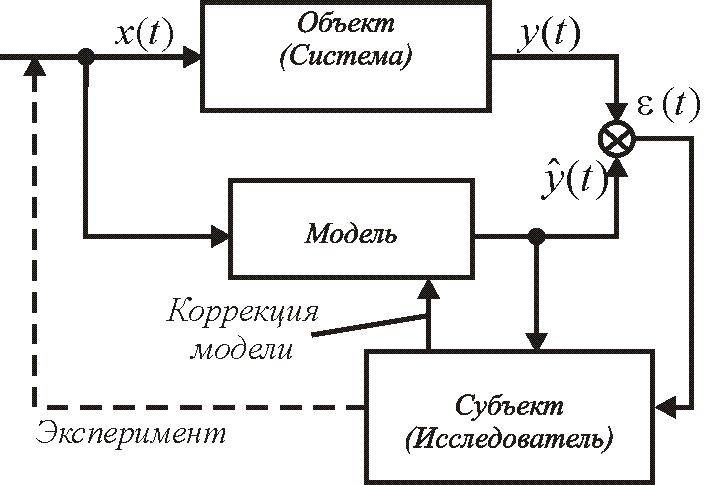
Рис. 1.1 Процесс познания объекта с помощью модели

Исследователь, имея определенные знания об объекте, строит первый вариант модели и путем сравнения с экспериментальными данными проверяет соответствие модели объекту. При необходимости ставятся специальные эксперименты и на основе анализа предсказанных и фактических реакций объекта , корректируются параметры или структура модели

Такие циклы обращений (субъект — модель — объект — субъект), составляющие восходящий спиралевидный процесс познания, осуществляют до тех пор, пока не будет получена некоторая модель , находящаяся в удовлетворительном соответствии с экспериментальными данными об объекте. Процесс построения модели с использованием эксперимента достаточно наглядно иллюстрируется структурной схемой [], приведенной на рис. 1.2.

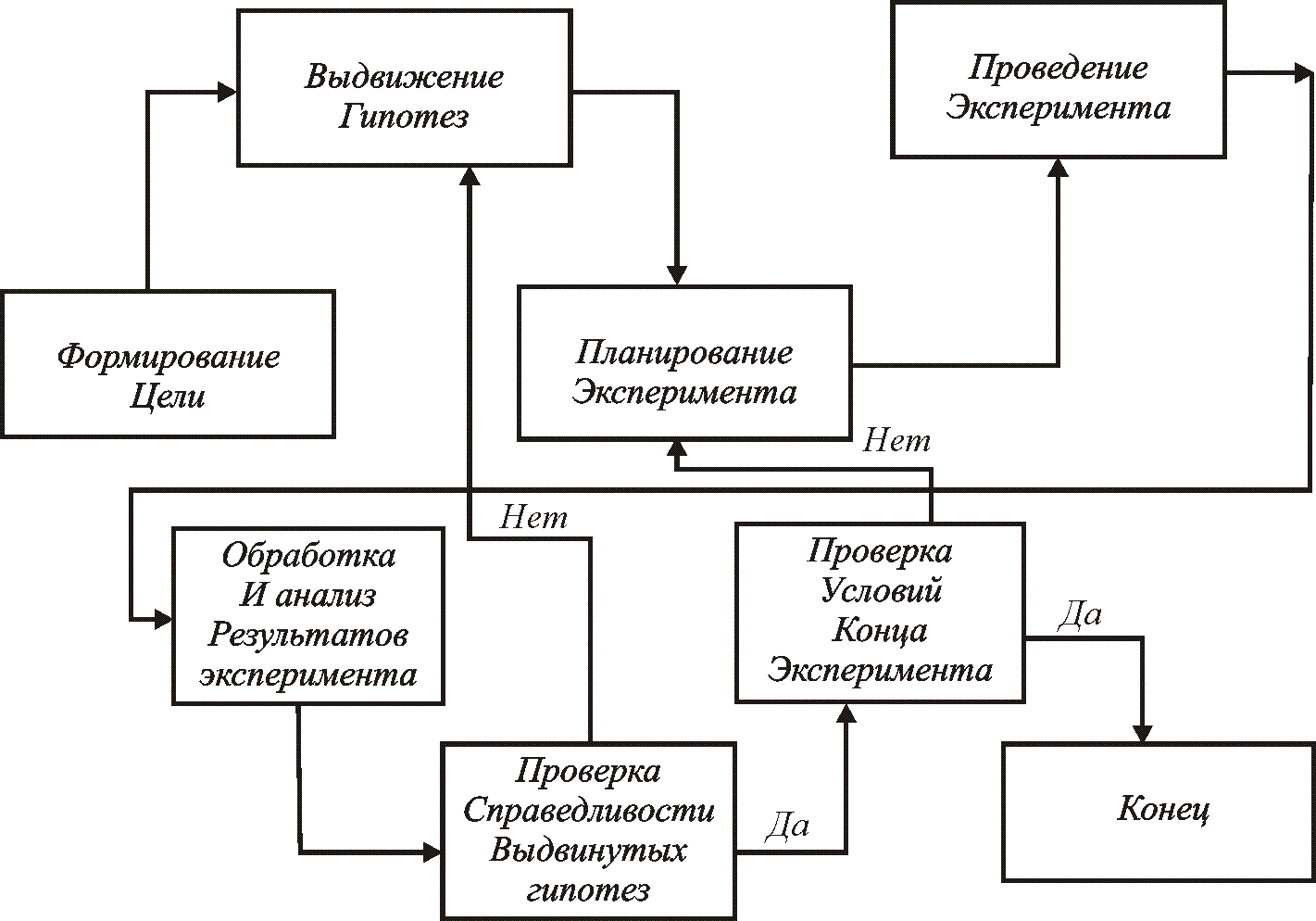
Рис. 1.2 Процесс построения модели с использованием эксперимента

Таким образом, моделирование можно рассматривать как развернутый во времени процесс экспериментального исследования, корректировки или смены моделей. Организация процесса моделирования аналогична оптимальному управлению, где критерием оптимальности является соотношение: потери от ошибочных решений — затрата на усложнение модели.

Большая ценность моделей как познавательного средства подчеркивается в целом ряде работ. На эвристический характер моделей, заданных в дифференциальных уравнениях, указывает, например, В. В. Налимов, который, являясь сторонником широкого применения статистических методов, в то же время признает большое значение моделей с гносеологической точки зрения, отмечая, что модель должна быть не только изящной, но и содержательной. Она должна хорошо объяснять известные факты, выявлять новые, ранее незамеченные явления, предсказывать их дальнейшее развитие, и, что может быть самое главное, выдвигать перед исследователем новые проблемы. Он же подчеркивает, что исходные модели в виде дифференциальных уравнений лучше осмысливаются, чем полиномиальныемодели.

В то же время необходимо отметить, что в целом ряде случаев для решения практических задач целесообразно использование полиномиальных моделей, построенных, например, с использованием экспериментально-статистических методов.

· Определение опорного плана (Это решение можно найти, используя метод «северо-западного угла» или метод «минимального элемента».)

· Нахождение оптимального решения путем последовательных операций. Методсеверо-западногоугла

Сущность метода заключается в том, что на каждом шаге заполняется левая верхняя (северо-западная) клетка оставшейся части таблицы, причем максимально возможным числом: либо полностью выносится груз из Аi, либо полностью удовлетворяется потребность Вj. Процедура продолжается до тех пор, пока на каком-то шаге не исчерпаются запасы аi и не удовлетворятся все потребности bj. В заключении проверяют, удовлетворяют ли найденные компоненты плана Х_ij горизонтальным и вертикальным уравнениям.

Методнаименьшегоэлемента

Сущность метода в том, что на каждом шаге заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф; в случае наличия нескольких таких равных тарифов заполняется любая из них. В остальном действуют аналогично предыдущему способу.

Методпотенциалов

Соотношения определяют систему из m+n-1 линейных уравнений с m+n известными, имеющую бесчисленное множество решений; для её определённости одному неизвестному присваивают произвольное значение (обычно альфа равное 0), тогда все остальные неизвестные определяются однозначно.

Критерий оптимальности

Если известны потенциалы решения Х0 транспортной задачи и для всех незаполненных ячеек выполняются условия б_i+в_j ? C_ij, то Х0 является оптимальным планом транспортной задачи.

Если план не оптимален, то необходимо перейти к следующему плану (таблице) так, чтобы транспортные расходы не увеличивались.

Цикл перерасчёта таблицы — это последовательность ячеек, удовлетворяющая условиям:

· Одна ячейка пустая, все остальные занятые.

· Любые две соседние ячейки находятся в одной строке или в одном столбце.

· Никакие три соседние ячейки не могут быть в одной строке или в одном столбце.

Пустой ячейке присваивают знак «+», остальным — поочерёдно знаки «-» и «+».

Для перераспределения плана перевозок с помощью цикла перерасчёта сначала находят незаполненную ячейку (r, s), в которой бr+вs > Crs, и строят соответствующий цикл; затем в минусовых клетках находят число X = min(X_ij). Далее составляют новую таблицу по следующему правилу:

· В плюсовых клетках добавляем Х.

· Из минусовых клеток вычитаем Х.

· Все остальные клетки вне цикла остаются без изменения.

Получим новую таблицу, дающую новое решение Х, такое, что F (X₁) ? F (X); оно снова проверяется на оптимальность через конечное число шагов, обязательно найдем оптимальный план транспортной задачи, ибо он всегда существует.

Выявление целей

Выявление целей. Первый и самый важный шаг при создании любой модели состоит в определении ее целевого назначения. Может быть применен метод декомпозиции целей, предполагающий разделение целого на части: целей – на подцели, задач – на подзадачи и т.д. На практике этот подход приводит к иерархическим древовидным структурам (построению дерева целей). Эта процедура является уделом специалистов и экспертов по проблеме. То есть, здесь присутствует субъективный фактор. Практическая задача состоит в том, насколько полно все структурировано. Построенное в результате этой процедуры дерево целей может в дальнейшем оказаться полезным при формировании множества критериев.

Какие подводные камни поджидают начинающего системного аналитика? То, что для одного уровня является целью, для другого уровня является средством, и часто происходит смешение целей. Для сложной системы с большим количеством подсистем цели могут быть противоречивыми. Цель редко бывает единственной, при множестве целей существует опасность неверного ранжирования.

Сформулированные и структурированные на первом этапе цели моделирования пронизывают весь ход дальнейшего имитационного исследования.

Рассмотрим наиболее употребляемые категории целей в имитационном исследовании: оценка, прогнозирование, оптимизация, сравнение альтернатив и др.

Эксперименты по моделированию проводятся с весьма разнообразными целями, в числе которых могут быть:

оценка – определение, насколько хорошо система предлагаемой структуры будет соответствовать некоторым конкретным критериям;
сравнение альтернатив – сопоставление конкурирующих систем, рассчитанных на выполнение определенной функции, или же на сопоставление нескольких предлагаемых рабочих принципов или методик;
прогноз – оценка поведения системы при некотором предполагаемом сочетании рабочих условий;
анализ чувствительности – выявление из большого числа действующих факторов тех, которые в наибольшей степени влияют на общее поведение системы;
выявление функциональных соотношений – определение природы зависимости между двумя или несколькими действующими факторами, с одной стороны, и откликом системы с другой;
оптимизация – точное определение такого сочетания действующих факторов и их величин, при котором обеспечивается наилучший отклик всей системы в целом.

Пример поэтапного построения модели

Постановка задачи

Создание модели процесса обезуглероживания металла в подовом сталеплавильном агрегате, изучение имеющихся на момент создания модели литературных данных позволило составить определенное представление о внутреннем механизме процесса обезуглероживания (рис.1.3).

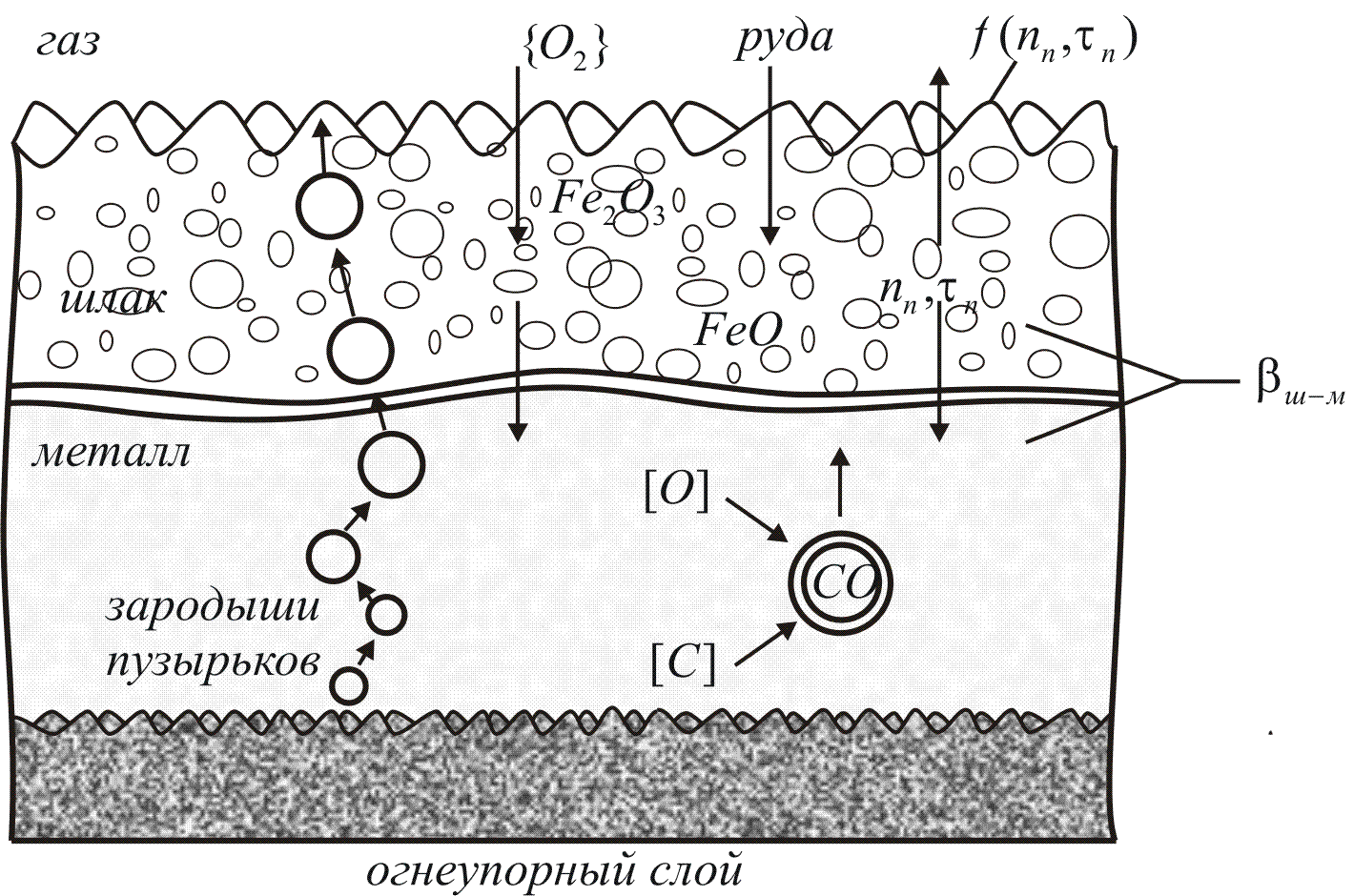
Рис. 1.3 Схема механизма процесса обезуглероживания

Газообразный кислород адсорбируется на верхней поверхности шлака

(1)

(2)

Внутри шлака происходит турбулентный перенос оксидов железа от верхней границы (газ-шлак) к нижней (шлак-металл), где при соприкосновении с металлом происходит восстановление высших оксидов до низших

(3)

(4)

параметры

(5)

Будем считать, что лимитирующей стадией в этом многостадийном процессе является доставка кислорода из газовой фазы и шлака в металл к месту реакции (пузырькам) путем конвективной (турбулентной) диффузии.

Так выглядит в данном примере первый этап моделирования – содержательная постановка задачи.

Выбор и построение модели

Структуризация

Таким образом, за основу механизма процесса обезуглероживания принято допущение о лимитирующей роли доставки кислорода к месту реакции. Далее сделаны следующие предположения.

Реакция окисления углерода

Поскольку скорость самой химической реакции значительно больше скорости диффузии, а скорость окисления углерода лимитируется скоростью подвода кислорода, то движущей силой диффузионного процесса является градиент концентраций кислорода.

Процесс передачи кислорода из газовой среды в металл можно рассматривать как ряд диффузионных звеньев, в каждом из которых кислород встречает более или менее значительное сопротивление (рис.1.4).

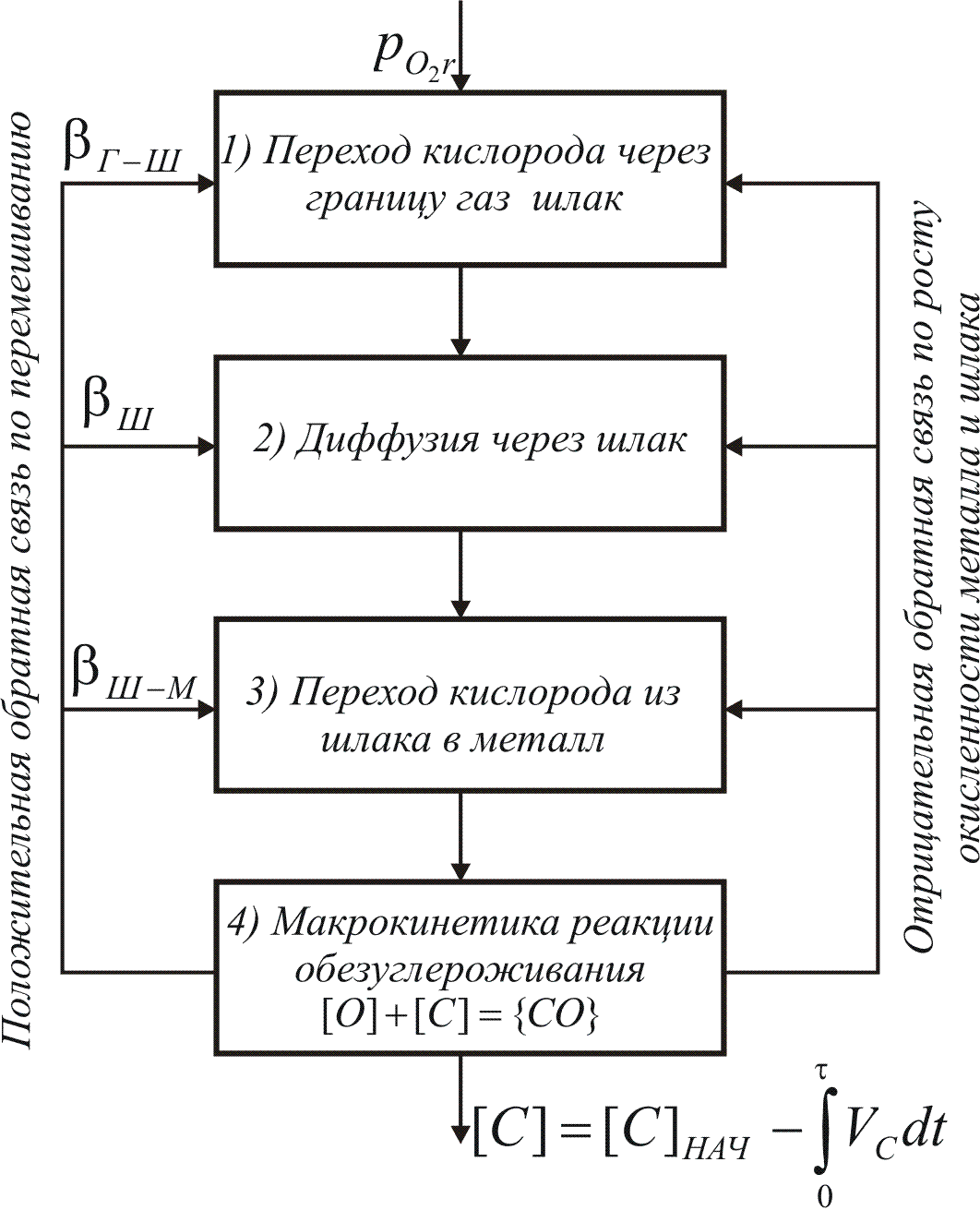
Рис. 1.4 Структуризация модели процесса обезуглероживания

Например:

преодоление границы газ – шлак;
диффузия кислорода через шлак;
преодоление границы шлак – металл и диффузия кислорода в металле к месту реакции;
реакция обезуглероживания и накопление кислорода в металле и шлаке.

Каждое такое звено можно, в свою очередь, представить состоящим из ряда элементарных звеньев.

Математическое описание структурных блоков

Уравнения диффузионных звеньев могут быть написаны на основе соотношения, выражающего скорость переноса вещества под влиянием молекулярной и турбулентной диффузии

– диффузионный поток вещества,

– падение концентрации вещества в направлении диффузии,

– константа скорости переноса,

Основу структурной схемы модели, представленной на рис.1.4, составляют уравнения диффузии, конкретизированные для отмеченных выше звеньев. Подробнее остановимся только на одном диффузионном звене, в котором рассматривается градиент концентраций от середины шлака до середины глубины ванны, и тогда скорость доставки кислорода (или скорость обезуглероживания) описывается уравнением следующего вида

– эффективный коэффициент массопереноса, являющийся функцией скорости обезуглероживания из-за перемешивающегося действия газообразного продукта реакции(5).

Реакция обезуглероживания и накопление в металле (с учетом предположения о приближении к термодинамическому равновесию) описывается уравнением вида

при

-влияние на процесс обезуглероживания расположения фронта преимущественного протекания реакции.

Участники процесса моделирования

Прежде всего необходимо подчеркнуть, что в этом процессе обязательно участвуют и взаимодействуют друг с другом субъект, объект исследования и модель. В связи с этим нельзя забывать, что в большинстве случаев моделям присуща определенная доля субъективизма, поскольку практически в процессе исследования приходится иметь дело не с самим объектом , а с представлениями о нем, т.е. с его моделью. Безусловно, по мере совершенствования модели и приближения ее к объекту объективная сторона модели становится преобладающей, происходит постепенное движение от относительной к абсолютной истине.

Технологические этапы создания и использования моделей

Вне зависимости от типа моделей (непрерывные и дискретные, детерминированные и стохастические и т.д.) имитационное моделирование включает в себя ряд основных этапов, представленных на рис. 3.1 и является сложным итеративным процессом:

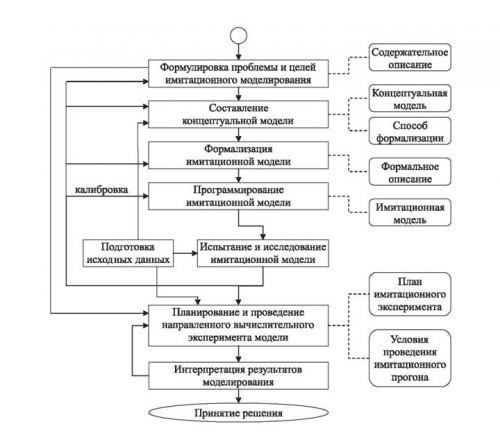
Рис. 3.1. Технологические этапы имитационного моделирования

1. Формулировка проблемы и определение целей имитационного исследования. Документированным результатом на этом этапе является составленное содержательное описание объекта моделирования;

2. Разработка концептуального описания. Результатом деятельности системного аналитика на этом этапе является концептуальная модель и выбор способа формализации для заданного объекта моделирования.

3. Формализация имитационной модели. Составляется формальное описание объекта моделирования.

4. Программирование имитационной модели (разработка программы-имитатора). Осуществляется выбор средств автоматизации моделирования, алгоритмизация, программирование и отладка имитационной модели.

5. Испытание и исследование модели, проверка модели. Проводится верификация модели, оценка адекватности, исследование свойств имитационной модели и другие процедуры комплексного тестирования разработанной модели.

6. Планирование и проведение имитационного эксперимента. Осуществляется стратегическое и тактическое планирование имитационного эксперимента. Результатом являются: составленный и реализованный план эксперимента, заданные условия имитационного прогона для выбранного плана.

7. Анализ результатов моделирования. Исследователь проводит интерпретацию результатов моделирования и их использование, собственно принятие решений.

Формулировка проблемы и определение целей имитационного исследования. На первом этапе формулируется проблема, стоящая перед исследователем и принимается решение о целесообразности применения метода имитационного моделирования. Затем определяются цели, которые должны быть достигнуты в результате имитации. От формулировки целей в значительной мере зависит выбор типа имитационной модели и характер дальнейшего имитационного исследования на имитационной модели. На этом этапе определяется и детально изучается объект моделирования, те стороны его функционирования, которые представляют интерес для исследования. Результатом работ на данном этапе является содержательное описание объекта моделирования с указанием целей имитации и тех аспектов функционирования объекта моделирования, которые необходимо изучить на имитационной модели. Содержательное описание составляется в терминологии реальной системы, на языке предметной области, понятном заказчику.

В ходе составления содержательного описания объекта моделирования устанавливаются границы изучения моделируемого объекта, дается описание внешней среды, с которой он взаимодействует. Формулируются основные критерии эффективности, по которым предполагается проводить сравнение на модели различных вариантов решений, проводится генерация и описание рассматриваемых альтернатив. Общего рецепта составления содержательного описания не существует. Успех зависит от интуиции разработчика и знания реальной системы. Общая технология или последовательность действий на этом этапе следующая: сбор данных об объекте моделирования и составление содержательного описания объекта моделирования; далее следует: изучение проблемной ситуации – определение диагноза и постановка задачи; уточнение целей моделирования; обосновывается необходимость моделирования и осуществляется выбор метода моделирования. На этом этапе четко и конкретно формулируются цели моделирования.

Цели моделирования определяют общий замысел модели и пронизывают все последующие этапы имитационного моделирования. Далее осуществляется формирование концептуальной модели исследуемого объекта.

Подробнее остановимся на основном содержании деятельности системного аналитика на этих ранних этапах. Эта работа важна для всех последующих этапов имитационного моделирования, именно здесь специалист по имитационному моделированию демонстрирует себя как системный аналитик, владеющий искусством моделирования.

Критерии эффективности

Критерии эффективности. Параметры, переменные модели. В описание системы должны быть включены критерии эффективности функционирования системы и оцениваемые альтернативные решения. Последние могут рассматриваться как входы модели или сценарные параметры. При алгоритмизации моделируемых процессов уточняются также основные переменные модели, участвующие в ее описании.

Каждая модель представляет собой некоторую комбинацию таких составляющих, как компоненты, переменные, параметры, функциональные зависимости, ограничения, целевые функции (критерии).

Под компонентами понимают составные части, которые при соответствующем объединении образуют систему. Иногда компонентами считают также элементы системы или ее подсистемы. Система определяется как группа или совокупность объектов, объединенных некоторой формой регулярного взаимодействия или взаимозависимости для выполнения заданной функции. Изучаемая система состоит из компонентов.

Параметрами являются величины, которые исследователь может выбирать произвольно, в отличие от переменных модели, которые могут принимать значения, определяемые видом заданной функции. В модели будем различать переменные двух видов: экзогенные и эндогенные. Экзогенные переменные называются также входными. Это означает, что они порождаются вне системы или являются результатом взаимодействия внешних причин. Эндогенными переменными называются переменные, возникающие в системе в результате воздействия внутренних причин. В тех случаях, когда эндогенные переменные характеризуют состояние или условия, имеющие место в системе, назовем их переменными состояния. Когда же необходимо описать входы и выходы системы, то имеем дело с входными и выходными переменными.

Функциональные зависимости описывают поведение переменных и параметров в пределах компоненты или же выражают соотношения между компонентами системы. Эти соотношения по природе являются либо детерминистскими, либо стохастическими.

Ограничения представляют собой устанавливаемые пределы изменения значений переменных или ограничивающие условия их изменений. Они могут вводиться либо разработчиком, либо устанавливаться самой системой вследствие присущих ей свойств.

Целевая функция (функция критерия) представляет собой точное отображение целей или задач системы и необходимых правил оценки их выполнения. Выражение для целевой функции должно быть однозначным определением целей и задач, с которыми должны соизмеряться принимаемые решения.

Формализация имитационной модели. На третьем этапе имитационного исследования осуществляется формализация объекта моделирования. Процесс формализации сложной системы включает:

выбор способа формализации;
составление формального описания системы.

В процессе построения модели можно выделить три уровня ее представления:

неформализованный (этап 2) – концептуальная модель;
формализованный (этап 3) – формальная модель;
программный (этап 4) – имитационная модель.

Каждый уровень отличается от предыдущего степенью детализации моделируемой системы и способами описания ее структуры и процесса функционирования. При этом уровень абстрагирования возрастает.

Аналитический способ представления задачи 1

Аналитический явный способ

Эта модель весьма далека от реальности. Что-либо изучить на ней представляется
проблематичным, так как из неё можно найти только время
T
и место встречи
S.
Идеализация заключается в том, что дорога считается идеально прямой, без
уклонов и подъёмов, скорости объектов считаются постоянными, желания объектов
не меняются, силы безграничны, отсутствуют помехи для движения, модель не
зависит от величин
D,
V₁,
V₂
(они могут быть сколь угодно большими или малыми).

T₁ := D/(V₁ + V₂)
S₁ := V₁ · T₁

Реальность обычно не имеет ничего общего с такой постановкой задачи. Но за счёт
большой идеализации (идеализации большого порядка) получается очень простая
модель, которая может быть разрешена в общем виде (аналитически)
математическими способами. Так формулируются чаще всего алгоритмические модели,
где протянута цепочка вычислений от исходных данных к выходу. Поэтому мы
применили в записи знак присваивания
(:=).
После вычисления правой части выражения её значение присваивается переменной,
стоящей в левой части. Далее значение этой переменной применено в правой части
следующего выражения. Схематически это выглядит так, как показано
на
рис. 1.18.

Рис. 1.18. Схема решения задачи о встрече(аналитический явный способ)

Аналитический неявный способ

В данной формулировке за счёт использования знака уравнивания получена связь
переменных
f(T, V₁, V₂, D, S) = 0
в виде системы уравнений. Устанавливая знак «?» на различные
переменные, можно формулировать при необходимости целый ряд произвольных задач,
например так:

T₁ · (V₁ + V₂) = D
S₁ = V₁ · T₁
T₁ = ?

При этом задачи формулируются пользователем и не предусматриваются специально
моделировщиком. То есть модель имеет вид объекта. Мы получили более
качественную модель. Идеализация её велика, но за счёт неявной формы записи
появилась возможность изменения задачи, изучения на ней целого ряда проблем.

Адекватность модели

Поскольку модель является выражением конечного ряда и только важнейших для
конкретного исследования аспектов сущности, то она не может быть абсолютно
идентичной моделируемому объекту. Кроме этого, реальный объект бесконечен для
познания. Поэтому нет смысла стремиться к бесконечной точности при построении
модели. Для выяснения необходимой степени адекватности обычно строят ряд
моделей, начиная с грубых, простых моделей и двигаясь ко все более сложным и
точным. Как только затраты на построение очередной модели начинают превышать
планируемую отдачу от модели, то уточнение модели прекращают. Первоначальные
шаги производятся в каком-либо существующем универсальном моделирующем пакете.
После одобрения модели под неё пишется специализированный пакет. Необходимость
в этом возникает в случае, если функционирование модели в универсальной среде
моделирования не удовлетворяет требованиям быстродействия (или каким-то другим).

В задачи данного курса входит изучение приёмов и способов, необходимых для
формализации, изучения и интерпретации систем.

Моделирование прикладная инженерная наука класса технологических.
Моделирование дисциплина, ставящая целью построение моделей и их
исследование посредством собственных универсальных методов, а также
специфических методов смежных с ней наук (математика, исследование операций,
программирование).

§ в G9 должна быть сумма ячеек B9: F9.

· Формулы для вычисления левых частей ограничений введем в ячейки B10: F10:

§ в B10 должна быть сумма ячеек B7: B9;

§ в C10 должна быть сумма ячеек C7: C9;

§ в D10 должна быть сумма ячеек D7: D9;

§ в E10 должна быть сумма ячеек E7: E9;

§ в F10 должна быть сумма ячеек F7: F9;

· Целевую функцию поместим в ячейку G2:

§ H4: СУММПРОИЗВ(B2:F4; B7:F9).

· Таблица исходных данных имеет вид (рис. 2.9.1):

Рисунок 2.9.1.

2) Заполнение окна процедуры «Поиск решения»

· Целевая функция: G2 ($G$2);

· Значение целевой функции: min;

· Изменяемые ячейки: B7: F9($B$7: $F$9);

· Ограничения задачи:

$B$10: $F410 = $B411: $F$11

$B$7: $F$9 = целое

$B$7: $F$90

$G$7: $G$9 = $H$7: $H$9

В окне «Параметры» установить «Линейная модель».

Результаты заполнения окна показаны на рис. 2.9.2.

Рисунок 2.9.2

3) Выполнив процедуру «Поиск решения» получим следующие результаты (рис. 2.9.3):

Рисунок 2.9.3

Таким образом из A1 следует отвезти 70 ед. товара в B1 и 80 ед. товара в B5; из A2 отвезти 30 ед. товара в B1, 90 ед. товара в B2 и 50 ед. товара в В4; из A3 отвезти 160 ед. товара в B3 и 100 ед. товара в B4. При этом суммарная стоимость транспортных расходов составит 3690 рубля.

Данная работа, может послужить примером материалов для самостоятельного изучения методов решения задач математического моделирования.

Я считаю, что цель поставленная в курсовой работе полностью достигнута, задачи выполнены, актуальность доказана.

Необходимо:

· Решить задачу геометрически (графики построить в системе Mathcad);

· Решить задачу симплекс-методом;

· Решить задачу программным способом с помощью табличного процессора MS Excel.

Таблица 1

Вид сырья	Продукция	Ограничения по сырью
	B₁	B₂
1-й	4	1	240
2-й	2	3	180
3-й	1	5	251
прибыль	40	30

Построение концептуальной модели

Построение концептуальной модели начинается с того, что на основе цели моделирования устанавливаются границы моделируемой системы, определяются воздействия внешней среды. Выдвигаются гипотезы и фиксируются все допущения (предположения), необходимые для построения имитационной модели. Обсуждается уровень детализации моделируемых процессов.

Можно определить систему есть совокупность взаимосвязанных элементов. В конкретной предметной области определение системы зависит от цели моделирования, и от того, кто определяет систему. На этом этапе осуществляется декомпозиция системы. Определяются наиболее существенные, в смысле сформулированной проблемы, элементы системы (выполняется структурный анализ моделируемой системы) и взаимодействия между ними, выявляются основные аспекты функционирования моделируемой систем (составляется функциональная модель), приводится описание внешней среды. Декомпозиция системы (объекта моделирования) или выделение подсистем – это операция анализа. Элементы модели должны соответствовать реально существующим фрагментам в системе. Сложная система разбивается на части, сохраняя при этом связи, обеспечивающие взаимодействие. Можно составить функциональную схему, которая прояснит специфику динамических процессов, происходящих в рассматриваемой системе

Важно определить, какие компоненты будут включены в модель, какие будут вынесены во внешнюю среду, и какие взаимосвязи будут установлены между ними

1.2 Характеристика типовых задач математического моделирования и подходов к их решению

Задачи моделирования делятся на две категории: прямые и обратные.

Прямыезадачи отвечают на вопрос, что будет, если при заданных условиях мы выберем какое-то решение из множества допустимых решений. В частности, чему будет равен, при выбранном решении критерий эффективности.

Обратныезадачи отвечают на вопрос: как выбрать решение из множества допустимых решений, чтобы критерий эффективности обращался в максимум или минимум.

Если число допустимых вариантов решения невелико, то можно вычислить критерий эффектности для каждого из них, сравнить между собой полученные значения и непосредственно указать один или несколько оптимальных вариантов. Такой способ нахождения оптимального решения называется «простым перебором». Когда число допустимых вариантов решения велико, то поиск оптимального решения простым перебором затруднителен, а зачастую практически невозможен. В этих случаях применяются методы «направленного» перебора, обладающие той особенностью, что оптимальное решение находится рядом последовательных попыток или приближений, из которых каждое последующие приближает нас к искомому оптимальному.

Модели принятия оптимальных решений отличаются универсальностью. Их можно классифицировать как задачи минимизации (максимизации) критерия эффективности, компоненты которого удовлетворяют системе ограничений (равенств и/или) неравенств.

Их можно разделить на:

принятие решений в условиях определенности — исходные данные — детерминированные; принятие решений в условиях неопределенности — исходные данные — случайныевеличины.

Таблица 1.2.1

Классификация задач оптимизации

Исходныеданные	Переменные	Зависимости	Задача
Детерминированные	Непрерывные	Линейные	Линейного программирования
	Целочисленные	Линейные	Целочисленного программирования
	Непрерывные, целочисленные	Нелинейные	Нелинейного программирования
Случайные	Непрерывные	Линейные	Стохастическое программирование

А по критерию эффективности:

· одноцелевое принятие решений (один критерий эффективности);

· многоцелевое принятие решений (несколько критериев эффективности).

Наиболее разработан и широко используется на практике аппарат одноцелевого принятия решений в условиях определенности, который получил название математического программирования. В этом «детерминированном» случаи, когда все условия операции известны заранее. тогда, обратная задача будет включает в себя критерий эффективности и некоторые известные заранее факторы (ограничения) позволяющие выбрать множество допустимых решений.

Вобщемвидеобратнаядетерминированнаязадачабудетвыглядетьследующимобразом.

Призаданномкомплексеограниченийнайтитакоеоптимальноерешение,принадлежащеемножествудопустимыхрешений,котороеобращаеткритерийэффективностивмаксимум(минимум).

Метод поиска экстремума и связанного с ним оптимального решения должен всегда исходить из особенности критерия эффективности и вида ограничений, налагаемых на решение.

Реальные задачи содержит помимо выше перечисленных факторов, еще одну группу — неизвестные факторы. Тогдаобратнуюзадачуможносформулироватьследующимобразом.

Призаданномкомплексеограничений,сучетомнеизвестныхфакторов,найтитакоеоптимальноерешение,принадлежащеемножествудопустимыхрешений,которое,повозможности,обеспечиваетмаксимальное(минимальное)значениекритерийэффективности.

Это уже другая, не чисто математическая задача. Наличие неопределенных факторов переводит эту задачу в новое качество: она превращается в задачу о выборе решений в условиях неопределенности.

Таблица 2.8.1

	v₁=2	v₂=10	v₃=15	v₄=22	v₅=25
u₁=0	2	10	15	14	4
u₂=-3	3	7	12	5	8
u₃=-9	21	18	6	13	16

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_i > c_ij(Табл. 2.8.1).

Выбираем максимальную оценку свободной клетки (1;5): 4

Для этого в перспективную клетку (1;5) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-» (Табл. 2.8.2).

Таблица 2.8.2

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2	10	15	14	4	150
A2	3	7	12	5	8	170
A3	21	18	6	13	16	260
Потребности	100	90	160	150	80	580

Цикл приведен в таблице (1,5; 1,2; 2,2; 2,3; 3,3; 3,5;).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е.

у = min (1, 2) = 50

Прибавляем 50 к объемам грузов, стоящих в плюсовых клетках и вычитаем 50 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план (Табл. 2.8.3).

Таблица 2.8.3

Пункт направления	B1	B2	B3	B4	B5	Запасы
1	2	10	15	14	4	150
2	3	7	12	5	8	170
3	21	18	6	13	16	260
Потребности	100	90	160	150	80	580

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

Таблица 2.8.4

	v₁=2	v₂=-11	v₃=-6	v₄=1	v₅=4
u₁=0	2	10	15	14	4
u₂=18	3	7	12	5	8
u₃=12	21	18	6	13	16

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_i > c_ij (Табл. 2.8.4).

Выбираем максимальную оценку свободной клетки (2;1): 3

Для этого в перспективную клетку (2;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-» (Табл. 2.8.5).

Таблица 2.8.5

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2	10	15	14	4	150
A2	3	7	12	5	8	170
A3	21	18	6	13	16	260
Потребности	100	90	160	150	80

Цикл приведен в таблице (2,1; 2,3; 3,3; 3,5; 1,5; 1,1;).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 5) = 30. Прибавляем 30 к объемам грузов, стоящих в плюсовых клетках и вычитаем 30 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план (Табл. 2.8.6).

Таблица 2.8.6

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2	10	15	14	4	150
A2	3	7	12	5	8	170
A3	21	18	6	13	16	260
Потребности	100	90	160	150	80	580

Таблица 2.8.7

	v₁=2	v₂=6	v₃=11	v₄=18	v₅=4
u₁=0	2	10	15	14	4
u₂=1	3	7	12	5	8
u₃=-5	21	18	6	13	16

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_i > c_ij(Табл. 2.8.7).

Выбираем максимальную оценку свободной клетки (2;4): 5

Для этого в перспективную клетку (2;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-» (Табл. 2.8.8).

Таблица 2.8.8

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2	10	15	14	4	150
A 2	3	7	12	5	8	170
A 3	21	18	6	13	16	260
Потребности	100	90	160	150	80	580

Цикл приведен в таблице (2,4; 2,3; 3,3; 3,4;).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 3) = 50. Прибавляем 50 к объемам грузов, стоящих в плюсовых клетках и вычитаем 50 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план (Табл. 2.8.9).

Таблица 2.8.9

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2	10	15	14	4	150
A2	3	7	12	5	8	170
A3	21	18	6	13	16	260
Потребности	100	90	160	150	80	580

Таблица 2.8.10

	v₁=2	v₂=6	v₃=-3	v₄=4	v₅=4
u₁=0	2	10	15	14	4
u₂=1	3	7	12	5	8
u₃=9	21	18	6	13	16

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_i <= c_ij(Табл. 2.8.10).

Минимальные затраты составят:

F(x) = 2*70 + 4*80 + 3*30 + 7*90 + 5*50 + 6*160 + 13*100 = 3690

Итерация № 0

Базис	Сб	X₁	X₂	X₃	X₄	X₅	Свободные члены	Отношение
X₃	4	1	1	240	240/4
X₄	2	3	1	180	180/2
X₅	1	5	1	251	251/1
Z	-40	-30	—

При составлении исходной симплекс таблицы (Табл. 2.3.1), коэффициенты при переменных функции ?? записываются с противоположными знаками, а свободный член со своим знаком.

Сб — вектор, составленный из координат соответствующих базисных переменных.

Текущий план не оптимален, так как в индексной строке находятся отрицательные коэффициенты.

Ведущий столбец X1, так как -40 — наименьшее отрицательное число.

За ведущую выберем строку 1, так как отношение свободного члена к соответствующему элементу выбранного столбца для 3 строки является наименьшим.

Таблица 2.3.2

Разрешающий элемент 4

Базис	Сб	X₁	X₂	X₃	X₄	X₅	Отношение
X₃	4	1/4	1/4	60	60
X₄	2	3	1	180	90
X₅	1	5	1	251	251
Z	-40	-30	—

От элементов строки 2 отнимаем соответствующие элементы строки 1, умноженные на 2.

От элементов строки 3 отнимаем соответствующие элементы строки 1, умноженные на 1.

От элементов строки ?? отнимаем соответствующие элементы строки 1, умноженные на -40 (Табл. 2.3.2)

Заменяем базисную переменную X3 на X1

Таблица 2.3.3

Итерация № 1

Базис	Сб	X₁	X₂	X₃	X₄	X₅	Свободные члены	Отношение
X₁	1	0,25	0,25	60	240
X₄	2,5	-0,5	1	60	24
X₅	40	4,75	-0,25	1	191	40,21
Z	-20	10	2400

Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты (Табл. 2.3.3).

За ведущий выберем столбец 2, так как -20 наименьший элемент в ?? строке.

За ведущую выберем строку 2, так как отношение свободного члена к соответствующему элементу выбранного столбца для 2 строки является наименьшим.

Разрешающий элемент 2,5

Разделим элементы строки 2 на 2,5(Табл. 2.3.3).

Таблица 2.3.4

Базис	Сб	X₁	X₂	X₃	X₄	X₅	Свободные члены	Отношение
X₁	1	0,25	0,25	60	240
X₄	20	1	-0,2	0,4	24	24
X₅	40	4,75	-0,25	1	191	40,21
Z	-20	10	2400

От элементов строки 1 отнимаем соответствующие элементы строки 2, умноженные на 0,25.

От элементов строки 3 отнимаем соответствующие элементы строки 2, умноженные на 4,75.

От элементов строки ?? отнимаем соответствующие элементы строки 2, умноженные на -20

Таблица 2.3.5

Базис	Сб	X₁	X₂	X₃	X₄	X₅	Свободные члены
X₁	1	0,3	-0,1	54
X₂	20	1	-0,2	0,4	24
X₅	40	0,7	-1,9	1	77
Z	6	8	2880

X2 = (54, 24, 77, 0, 0)

??(X2) = 40*54 + 30*24 = 2880 (Табл. 2.3.5).

Ответ:Для достижения максимальной прибыли 2880 ден.ед. следует производить 54 ед. продукции вида А1 и 24 ед. продукции вида А2. (ответ совпадает с ответом полученным графическим способом).