Вырожденный газ

Классификация элементарных частиц

кварков. Согласно теории Цвейга–Гелл-Манна все известные к тому времени адроны можно было построить, постулировав существование трех типов кварков: u (от англ. “up”, т.е. “вверх”), d (down – вниз) и s (strange – странный или sideways – боковой) и соответствующих им антикварков. Кварки обладают дробным электрическим зарядом, полуцелым спином (т.е. являются фермионами) и рядом других характеристик. Мезоны состоят из пары кварк–антикварк, барионы из трех кварков (например, протон имеет кварковую структуру uud). Кварки существуют только внутри адронов и не наблюдаются как изолированные объекты.

Увеличение числа элементарных частиц привело к необходимости расширения системы кварков. Пришлось постулировать существование еще трех кварков: с (charmed – очарованный), b (bottom – нижний или beauty – прелестный) и t (truth – истинный).

Реальное существование кварков подтверждается рядом экспериментальных фактов. Так, характер рассеяния быстрых электронов протонами свидетельствует о наличии внутри протона трех точечных рассеивающих центров с дробным электрическим зарядом, что полностью соответствует трехкварковой модели протона.

Все попытки наблюдать кварки как изолированные объекты оказались безуспешными, они в принципе не могут существовать в свободном состоянии. Применительно к кваркам даже существует термин конфайнмент (от английского confinement, что означает “тюремное заключение”). Причиной конфайнмента является необычное поведение сил взаимодействия кварков друг с другом.

При малых расстояниях эти силы малы, однако с увеличением расстояния силы взаимодействия между кварками очень быстро растут, не позволяя кваркам вылететь из адрона.

В наши дни принята Стандартная модель, по которой всё вещество состоит из 24 частиц-фермионов: 6 лептонов, 6 кварков и 12 античастиц. Частицами-переносчиками взаимодействий являются 8 глюонов, 3 тяжёлых бозона, один фотон. Теоретически предсказано существование бозона Хиггса, отвечающего за массу.

Контрольные вопросы

1 Как развивались представления о строении атома?

2 Сформулируйте постулаты Бора.

3 Каковы основные результаты решения уравнения Шредингера для атома водорода?

4 Какие физические величины, характеризующие состояние электрона в атоме, оказываются дискретными?

5 Какие квантовые числа Вы знаете? Что они характеризуют?

6 Когда атом поглощает или излучает энергию? Запишите закон сохранения энергии для элементарного акта излучения или поглощения.

7 Какие частицы называются в квантовой теории тождественными? В чем заключается принцип неразличимости тождественных частиц?

8 Сформулируйте принцип Паули. Поведение каких систем объясняется этим принципом?

9 Из каких элементарных частиц состоит атомное ядро?

10 Что такое дефект массы и энергия связи ядра? Какие ядра обладают наибольшей энергией связи?

11 Перечислите свойства ядерных сил.

12 Что такое радиоактивность?

13 Запишите закон радиоактивного распада. Каков физический смысл периода полураспада?

14 Приведите примеры α-распада и β-распада.

15 Какова причина возникновения γ-излучения?

16 Сравните радиоактивные излучения по проникающей и ионизирующей силе.

17 Охарактеризуйте основные типы фундаментальных взаимодействий

18 Какие частицы называются элементарными? Как они классифицируются?

19 Что такое кварки?

Модуль 3Химические основы технологий

3.1Элементы современной химии

Предыдущая45464748495051525354555657585960Следующая

Дата добавления: 2016-01-26; просмотров: 1013;

Уравнение состояния вырожденного ферми газа

В этой модели рассматривается движение невзаимодействующих друг с другом нуклонов в области объемом V, в пределах которой потенциал считается постоянным. Одночастичные состояния нейтронов и протонов описываются плоскими волнами , где — спиновая функция нуклона, характеризующая величину проекции спина ( = ± 1/2) на ось квантования z, — импульс нуклона, — его радиус вектор и = 6,5820·10 -22 МэВ·сек — перечеркнутая постоянная Планка. Строго говоря, предположение, что одночастичные волновые функции имеют вид плоских волн, справедливо только для ядра, радиус которого R . Однако, если мы не рассматриваем влияние ядерной поверхности, оно может быть использовано и для конечного ядра. При этом необходимо учитывать, что в ограниченном объеме V возможен только дискретный набор значений вектора импульса = x, p_y, p_z >. Нужные собственные значения импульса и кинетической энергии нуклона E = p 2 /(2m) (m — масса нуклона) можно найти, вводя периодические граничные условия:

(x,y,z) = (x+L,y,z) = (x,y+L,z) = (x,y,z+L),

где L — длина ребра куба, имеющего объем V. Эти граничные условия дают собственные значения

px = (2 π /L)nx, py = (2 π /L)ny, pz = (2 π /L)nz,

где n_x, n_y, n_z — целые числа равные 0, ± 1, ± 2, ± 3. и m — масса нуклона. На каждом нейтронном (или протонном) уровне могут в соответствии с принципом Паули находится только два нейтрона (или протона), имеющие разные проекции спина (см. рис. 2.1). В основном состоянии ядра N нейтронов и Z протонов занимают самые низшие энергетические уровни. Граница, разделяющая заполненные и незаполненные одночастичные уровни, называется границей (уровнем) Ферми. Отвечающие ей максимальные величины импульсов для нейтронов и протонов обозначаются символами и . Максимальная кинетическая энергия называется энергией Ферми. Она равна

для нейтронов и протонов, соответственно.

Рис. 2.1. Нейтронные и протонные одночастичные уровни энергии в модели ферми-газа. Протонная потенциальная яма мельче, чем нейтронная яма, из-за действия кулоновских сил (E_С — кулоновская энергия протона). Эти же силы обуславливают возникновение кулоновского барьера для протонов, которые стремятся вылететь из ядра или проникнуть в него снаружи. B_N — энергия отделения нейтрона.

Элемент объекта в импульсном пространстве d 3 p = dp_xdp_ydp_z в сферической системе координат можно записать в виде d 3 p = р 2 sin θ dpd φ d θ . Если ориентация вектора p не существенна, то интегрирование по углам дает d 3 p = 4 π p 2 dp. Согласно (2.1) среднее число одночастичных состояний нейтрона или протона (d 3 n = dn_xdn_ydn_z) в элементе импульсного пространства d 3 p дается выражением

d 3 n = [2·4 π Vp 2 /(2 π ) 3 ]dp = (8 π Vp 2 /h 3 )dp,

где множитель 2 учитывает две возможные ориентации спина нуклона. Поэтому полное число нейтронов и протонов в ядре может быть представлено в виде

Вырождение Ферми- и Бозе-газов

Зависимость давления вырожденного ферми-газа от температуры, сохранению состояния вырождения соответствует горизонтальная ветвь.

Тип вырождения различен для частиц с полуцелым спином (фермионов, статистика Ферми — Дирака) и частиц с целым спином (бозонов, статистика Бозе — Эйнштейна), соответственно различаются и свойства ферми- и бозе-газов.

Если для Ферми-газа вследствие действия принципа Паули давление вырожденного газа выше давления идеального газа в тех же условиях, то для вырожденного Бозе-газа давление ниже давления идеального газа вследствие конденсации Бозе — Эйнштейна.

У ферми-газа (к которому относится электронный газ в металле) при полном вырождении (при ) заполнены все нижние энергетические уровни вплоть до некоторого максимального, называемого уровнем Ферми, а все последующие остаются пустыми. Повышение температуры лишь незначительно изменяет такое распределение электронов металла по уровням: малая доля электронов, находящихся на уровнях, близких к уровню Ферми, переходит на пустые уровни с большей энергией, освобождая таким образом уровни ниже фермиевского, с которых был совершен переход.

При вырождении газа бозонов из частиц с отличной от нуля массой (такими бозонами могут быть атомы и молекулы) некоторая доля частиц системы должна переходить в состояние с нулевым импульсом; это явление называется Бозе — Эйнштейновской конденсацией. Чем ближе температура к абсолютному нулю, тем больше частиц должно оказаться в этом состоянии. Однако, системы таких частиц при понижении температуры до очень низких значений переходят в твёрдое или жидкое (для гелия) состояния, к которым неприменимо приближение идеального газа.

Для газа из бозонов нулевой массы, к которым относятся фотоны, температура вырождения равна бесконечности; поэтому фотонный газ всегда вырожденный, и классическая статистика к нему не применима. Фотонный газ является единственным вырожденным идеальным бозе-газом стабильных частиц. Однако Бозе-Эйнштейновской конденсации в нём не происходит, так как не существует фотонов с нулевым импульсом (фотоны всегда движутся со скоростью света).

Явление вырождения Ферми-газов играет важную роль в эволюции звёзд: так, давление электронного вырожденного газа уравновешивает тяготение в белых карликах, а давление нейтронного вырожденного газа уравновешивает тяготение в нейтронных звёздах.

Связанные величины Ферми

Некоторые полезные величины, связанные с энергией Ферми, также часто встречаются в современной литературе.

Температура Ферми определяется как , где — постоянная Больцмана . Температуру Ферми можно рассматривать как температуру, при которой тепловые эффекты сравнимы с квантовыми эффектами, связанными со статистикой Ферми. Температура Ферми для металла на пару порядков выше комнатной. Другие величины , определенные в данном контексте являются импульсом Ферми и скорость Ферми , которые являются импульсом и групповой скоростью , соответственно, из фермиона на поверхности Ферми . Импульс Ферми также можно описать как , где — радиус сферы Ферми и называется волновым вектором Ферми .
ТFзнак равноEFkB{\ displaystyle T _ {\ mathrm {F}} = {\ frac {E _ {\ mathrm {F}}} {k _ {\ rm {B}}}}}kB{\ Displaystyle к _ {\ rm {B}}} пFзнак равно2мEF{\ displaystyle p _ {\ mathrm {F}} = {\ sqrt {2mE _ {\ mathrm {F}}}}} vFзнак равнопFм{\ displaystyle v _ {\ mathrm {F}} = {\ frac {p _ {\ mathrm {F}}} {m}}}пFзнак равноℏkF{\ displaystyle p _ {\ mathrm {F}} = \ hbar k _ {\ mathrm {F}}}kF{\ Displaystyle к _ {\ mathrm {F}}}

Обратите внимание, что эти величины не определены должным образом в случаях, когда поверхность Ферми не является сферической.

Дополнения к модели

Релятивистский ферми-газ

Соотношения радиуса и массы для модельного белого карлика, релятивистское соотношение против нерелятивистского. Чандрасекаровский предел обозначается как M _Ch .

В статье рассматривается только случай, когда частицы имеют параболическую связь между энергией и импульсом, как это имеет место в нерелятивистской механике. Для частиц с энергиями, близкими к их массе покоя , применимы уравнения специальной теории относительности . Где одночастичная энергия определяется как:

Eзнак равно(пc)2+(мc2)2{\ displaystyle E = {\ sqrt {(pc) ^ {2} + (mc ^ {2}) ^ {2}}}}.

Для этой системы энергия Ферми определяется выражением:

EFзнак равно(пFc)2+(мc2)2-мc2≈пFc{\ displaystyle E _ {\ mathrm {F}} = {\ sqrt {(p _ {\ mathrm {F}} c) ^ {2} + (mc ^ {2}) ^ {2}}} — mc ^ {2 } \ приблизительно p _ {\ mathrm {F}} c},

где равенство справедливо только в ультрарелятивистском пределе , и
≈{\ Displaystyle \ приблизительно}

пFзнак равноℏ(1граммs6π2NV)13{\ displaystyle p _ {\ mathrm {F}} = \ hbar \ left ({\ frac {1} {g_ {s}}} 6 \ pi ^ {2} {\ frac {N} {V}} \ right) ^ {1/3}}.

Модель релятивистского ферми-газа также используется для описания больших белых карликов, близких к пределу Чандрезекара. Для ультрарелятивистского случая давление вырождения пропорционально .
(NV)43{\ Displaystyle (Н / В) ^ {4/3}}

Ферми жидкость

В 1956 году Лев Ландау разработал теорию ферми-жидкости , в которой он рассмотрел случай ферми-жидкости, т. Е. Системы с отталкивающими, не обязательно малыми взаимодействиями между фермионами. Теория показывает, что термодинамические свойства идеального ферми-газа и ферми-жидкости не сильно различаются. Можно показать, что ферми-жидкость эквивалентна ферми-газу, состоящему из коллективных возбуждений или квазичастиц , каждая из которых имеет различную эффективную массу и магнитный момент .

Элементарные частицы и их классификация. Понятие о кварках

Элементарной называется частица, которая на современном уровне развития науки не обнаруживает внутреннего строения, а ее размеры недоступны измерению. Фундаментальным свойством всех элементарных частиц является их способность к взаимному превращению. Элементарные частицы принято классифицировать по тому типу взаимодействия, в которое они вступают и по значению их собственного момента импульса (спина).

По типу характерных для частиц взаимодействий они делятся на четыре класса.

1 Фотоны – кванты электромагнитного поля, участвуют в электромагнитном взаимодействии, но не обладают сильным и слабым.

2 Лептоны – частицы, не обладающие сильным взаимодействием (электрон, позитрон, мюон, нейтрино, антинейтрино и др.). Все лептоны участвуют в слабом взаимодействии, заряженные лептоны участвуют также в электромагнитном взаимодействии.

3Мезоны – сильно взаимодействующие нестабильные частицы, участвуют также в слабом и электромагнитном взаимодействии (p-мезон, К-мезон и др.)

4 Барионы – частицы, обладающие сильным взаимодействием (протон, нейтрон, все гипероны). Заряженные барионы участвуют также в электромагнитном взаимодействии.

Мезоны и барионы часто объединяют в один класс сильно взаимодействующих частиц, называемых адронами.

По значению собственного момента импульса (спина) элементарные частицы делятся на два класса:

1 Фермионы – частицы с полуцелым спином, описывающиеся антисимметричными волновыми функциями и подчиняющиеся статистике Ферми–Дирака (электрон, протон, нейтрон и др.).

2 Бозоны – частицы с нулевым или целочисленным спином, описывающиеся симметричными волновыми функциями и подчиняющиеся статистике Бозе–Эйнштейна (p-мезон, фотон).

Все лептоны и барионы являются фермионами, а мезоны и фотон – бозонами. Для фермионов справедлив принцип Паули, согласно которому в системе тождественных фермионов не может быть двух частиц, обладающих одинаковым набором квантовых чисел. Ранее мы сформулировали этот принцип для электронов в атоме и объяснили с его помощью заполнение электронных оболочек атомов (Периодическая система элементов Д.И. Менделеева). Однако принцип Паули имеет более широкую область применения, ему подчиняется поведение любых коллективов тождественных фермионов (атомное ядро, электронный газ в металлах и т.д.). Для коллектива бозонов принципа запрета Паули нет.

Все переносчики взаимодействий являются бозонами, а кварки и лептоны – фермионами. В связи с этим бозоны принято ассоциировать с взаимодействием, а фермионы – с веществом. Суперсимметрия объединяет фермионы и бозоны в рамках одной теории и говорит о возможности превращения бозонов и фермионов друг в друга.

Использование термина “элементарные” становится неоправданным, когда мы говорим о почти 400 частицах и античастицах, открытых к настоящему времени. Развитие работ по классификации частиц все время сопровождалось поисками новых более фундаментальных частиц, из которых построены все адроны (барионы и мезоны). В 1964 г. независимо друг от друга Дж. Цвейг и Гелл-Манн высказали гипотезу о существовании т.н.

Вырожденный газ в природе

Электронный вырожденный газ обычно встречается в белых карликах, образуя ядро звезды, в результате сильного давления со стороны ее верхних слоев. Так как электроны – это фермионы, то они подчиняются принципу Паули – несколько фермионов не могут находиться в одном состоянии (в т. ч. в одной точке). По этой причине внешние слои звезды способны сжать электронный газ лишь до определенного объема.

В случае коллапса звезды – она превращается в нейтронную. В таком случае, под давлением верхних слоев атмосферы электроны «сливаются» с протонами, вследствие чего превращаются в нейтральные частицы – нейтроны. Далее нейтроны сжимаются массой звезды до высокой степени вырождения, образуя нейтронный вырожденный газ.

Строение нейтронной звезды

Понравилась запись? Расскажи о ней друзьям!

Принцип тождественности

Говоря о принципе тождественности частиц – это одно из основных различий между квантовой и классической механикой. Его суть состоит в том, что в классической механике всегда можно проследить за траекторией тела, а потому и явно отличить одно тело от другого с течением времени. В случае же с квантовым миром, наблюдение одной частицы невозможно, так как она не имеет определенной траектории, а распространяется в соответствии с волнами де Бройля. Это волны вероятности, которые определяют вероятность обнаружения частицы в заданной точке пространства.

Таким образом, если нельзя отследить траекторию некоторой частицы, то нельзя и утверждать, что с течением времени мы наблюдаем одну и ту же частицу, а не другую частицу того же сорта.

Область возможного обнаружения электрона вокруг ядра

1D однородный газ

Одномерная бесконечная квадратная яма длиной L представляет собой модель одномерного ящика с потенциальной энергией:

V(Икс)знак равно{,Иксc-L2<Икс<Иксc+L2,∞,иначе.{\ displaystyle V (x) = {\ begin {cases} 0, & x_ {c} — {\ tfrac {L} {2}} <x <x_ {c} + {\ tfrac {L} {2}}, \\\ infty, & {\ text {в противном случае.}} \ end {case}}}

Это стандартная модельная система в квантовой механике, для которой хорошо известно решение для отдельной частицы. Поскольку потенциал внутри ящика однороден, эту модель называют одномерным однородным газом, даже несмотря на то, что фактический профиль числовой плотности газа может иметь узлы и пучности, когда общее количество частиц невелико.

Уровни помечены одним квантовым числом n, а энергии даны как:

Eпзнак равноE+ℏ2π22мL2п2.{\ displaystyle E_ {n} = E_ {0} + {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} n ^ {2}. \,}

где — энергия нулевой точки (которая может быть выбрана произвольно в качестве формы фиксации калибровки ), масса одного фермиона и — приведенная постоянная Планка .
E{\ displaystyle E_ {0}}м{\ displaystyle m}ℏ{\ displaystyle \ hbar}

Для N фермионов со спином 1/2 в ящике не более двух частиц могут иметь одинаковую энергию, т. Е. Две частицы могут иметь энергию , две другие частицы могут иметь энергию и так далее. Две частицы с одинаковой энергией имеют спин ½ (спин вверх) или −½ (спин вниз), что приводит к двум состояниям для каждого уровня энергии. В конфигурации, для которой полная энергия самая низкая (основное состояние), все уровни энергии до n  =  N / 2 заняты, а все более высокие уровни пусты.
E1{\ textstyle E_ {1}}E2{\ textstyle E_ {2}}

Определяя эталон для энергии Ферми как , энергия Ферми, следовательно, дается выражением
E{\ displaystyle E_ {0}}

EF(1D)знак равноEп-Eзнак равноℏ2π22мL2(⌊N2⌋)2,{\ displaystyle E _ {\ mathrm {F}} ^ {({\ text {1D}})} = E_ {n} -E_ {0} = {\ frac {\ hbar ^ {2} \ pi ^ {2} } {2mL ^ {2}}} \ left (\ left \ lfloor {\ frac {N} {2}} \ right \ rfloor \ right) ^ {2},}

где — функция пола, оцененная при n  =  N / 2.
⌊N2⌋{\ displaystyle \ left \ lfloor {\ frac {N} {2}} \ right \ rfloor}

Термодинамический предел

В термодинамическом пределе общее число частиц N настолько велико, что квантовое число n можно рассматривать как непрерывную переменную. В этом случае общий профиль числовой плотности в коробке действительно однороден.

Количество квантовых состояний в диапазоне :
п1<п<п1+dп{\ displaystyle n_ {1} <n <n_ {1} + \ operatorname {d} \! n}

Dп(п1)dпзнак равно2dп.{\ displaystyle D_ {n} (n_ {1}) \ operatorname {d} \! n = 2 \ operatorname {d} \! n \ ,.}

Без ограничения общности энергия нулевой точки выбрана равной нулю, что дает следующий результат:

Eпзнак равноℏ2π22мL2п2⟹dEзнак равноℏ2π2мL2пdпзнак равноℏπL2Eмdп.{\ displaystyle E_ {n} = {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} n ^ {2} \ подразумевает \ operatorname {d} \! E = { \ frac {\ hbar ^ {2} \ pi ^ {2}} {mL ^ {2}}} n \ operatorname {d} \! n = {\ frac {\ hbar \ pi} {L}} {\ sqrt {\ frac {2E} {m}}} \ operatorname {d} \! n \ ,.}

Поэтому в ассортименте:

E1знак равноℏ2π22мL2п12<E<E1+dE,{\ displaystyle E_ {1} = {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} n_ {1} ^ {2} <E <E_ {1} + \ имя оператора {d} \! E \ ,,}

количество квантовых состояний:

Dп(п1)dпзнак равно2dEdEdпзнак равно2ℏ2π2мL2пdE≡D(E1)dE.{\ displaystyle D_ {n} (n_ {1}) \ operatorname {d} \! n = 2 {\ frac {\ operatorname {d} \! E} {\ operatorname {d} \! E / \ operatorname {d } \! n}} = {\ frac {2} {{\ frac {\ hbar ^ {2} \ pi ^ {2}} {mL ^ {2}}} n}} \ operatorname {d} \! E \ Equiv D (E_ {1}) \ operatorname {d} \! E \ ,.}

Здесь степень вырожденности равна:

D(E)знак равно2dEdпзнак равно2Lℏπм2E.{\ displaystyle D (E) = {\ frac {2} {\ operatorname {d} \! E / \ operatorname {d} \! n}} = {\ frac {2L} {\ hbar \ pi}} {\ sqrt {\ frac {m} {2E}}} \ ,.}

А плотность состояний равна:

грамм(E)≡1LD(E)знак равно2ℏπм2E.{\ displaystyle g (E) \ Equiv {\ frac {1} {L}} D (E) = {\ frac {2} {\ hbar \ pi}} {\ sqrt {\ frac {m} {2E}} } \ ,.}

В современной литературе это иногда еще называют «плотностью состояний». Однако отличается от фактора объемом системы (который в этом одномерном случае).
D(E){\ Displaystyle D (E)}грамм(E){\ displaystyle g (E)}D(E){\ Displaystyle D (E)}L{\ displaystyle L}

На основе следующей формулы:

∫EFD(E)dEзнак равноN,{\ Displaystyle \ int _ {0} ^ {E_ {F}} D (E) dE = N \ ,,}

энергия Ферми в термодинамическом пределе может быть рассчитана как:

EF(1D)знак равноℏ2π22мL2(N2)2.{\ displaystyle E _ {\ mathrm {F}} ^ {({\ text {1D}})} = {\ frac {\ hbar ^ {2} \ pi ^ {2}} {2mL ^ {2}}} \ left ({\ frac {N} {2}} \ right) ^ {2} \ ,.}

Фоновые шумы

Надо понимать, что «ловить» гравитационные волны невероятно тяжело. Они возникают, например, тогда, когда сталкиваются, а затем сливаются друг с другом две чёрные дыры. По своей сути это что-то вроде ряби на воде,которая колеблет Землю на ширину всего лишь одного атомного ядра. Этот факт объясняет, почему вызвало такой ажиотаж заявление LIGO об их обнаружении, не правда ли?

Тем не менее, мимолётность явления — это не единственная проблема. Детекторы обсерваторий должны быть невероятно чувствительными — это чистая правда. Но,кроме того, учёные должны отделять гравитационные волны от беспрестанного фонового шума, который может создаваться в том числе и естественной вибрацией самой Земли. Поэтому у LIGO есть два совершенно независимых друг от друга комплекса — один в Луизиане, второй в штате Вашингтон. Между этими детекторами почти целый континент — посторонние шумы на таком расстоянии не должны, по идее,фиксироваться одновременно, в то время как гравитационные волны будут выглядеть идентично на мониторах исследователей на обоих объектах.

Особенности бозонов

Совокупности тождественных бозонов описывают, используя симметричную волновую функцию ($?$), которая подчиняется квантовой статистике Бозе — Эйнштейна.

Любое число бозонов может находиться в одном состоянии.

Среди бозонов выделяют элементарные и составные.

Элементарными бозонами являются кванты калибровочных полей. При помощи этих квантов элементарные фермионы (лептоны и кварки) реализуют свои взаимодействия, если рассматривать стандартную модель. Элементарными бозонами считают фотоны, при помощи которых осуществляется электромагнитное взаимодействие. Примером элементарных бозонов являются глюоны, которые реализуют сильное взаимодействие. W и Z бозоны, отвечают за слабое взаимодействие. И так, элементарные бозоны переносят взаимодействие.

Элементарными бозонами на сегодняшний момент являются: 4 калибровочных бозона (фотон, $W^{\pm }$ и Z бозоны), 8 глюонов.

Кроме W бозона все элементарные бозоны не имеют заряда. $W^+$ и $W^-$ бозоны — это античастицы. Спины фотона, глюона, $W^+$ и $W^-$ бозонов, Z — бозона равны единице. Гравитон обладает спином равным двум, бозон Хиггса несет нулевой спин.

К составным бозонам относят множество двухкварковых мезонов. Спин мезонов равен целому числу, и оно не имеет ограничения. Ядра атомов, которые обладают нечетным количеством нуклонов, так же являются бозонами.

И всё-таки они существуют

Ладно, довольно на сегодня интриг, скандалов, расследований и дамских сериалов. Всё совсем не так печально, как вам могло показаться. Когда пыль от столкновения датских и американских учёных осядет, публиковать опровержения новостей об обнаружении гравитационных волн никому не придётся. Каяться за них тоже. Они действительно найдены. Вопрос не в том, что учёные из LIGO всех обманывают, а в том, что методы их анализа нуждаются в улучшении. Так как если они будут применяться и дальше, возможны ошибки, которые недопустимы в столь серьёзных вопросах.Это научный процесс в чистом виде, господа! В данный момент времени LIGO занимается составлением подробного отчёта, описывающего, каким именно образом учёные получили свои результаты. Кроме того, совсем недавно, в начале декабря,появились сообщения о том, что этот коллектив, анализируя ранее полученные данные, обнаружил слияния ещё четырёх пар чёрных дыр. Эти столкновения были не такими «громкими», поэтому потребуют более тщательного изучения. Так что давайте просто дождёмся публикации, которую готовят американские исследователи. Возможно, все вопросы относительно корректности их методов после этого исчезнут сами по себе.

Датские скептики

Таким образом, согласно концепции, отсеивать шум должно быть сравнительно просто — надо убрать все те сигналы, которые не совпадают на севере и юге США. После этого на экранах должны остаться только гравитационные волны. Но это в идеале. И именно здесь начинается «дружеская» дискуссия в узком научном кругу. Группа физиков из института Нильса Бора, что в Копенгагене, провела собственный анализ данных, которые учёные LIGO по доброте душевной выкладывают в общий доступ, и у неё сразу же возникли вопросы относительно методов обработки информации, использованных американцами.

У датчан получилось, что полное совпадение наблюдается не только у»гравитационных волн», но и у некоторых посторонних шумов. И, по их мнению, это значит, что LIGO выдаёт за рябь от столкновения чёрных дыр, мягко говоря, нечто не до конца понятное. Европейцы донесли свои сомнения до заокеанских коллег. Те с небольшим раздражением ответили, что методы и компьютерные программы, которые они используют для извлечения оригинальных данных, крайне сложны в практическом применении и, возможно, именно поэтому датские учёные всё неправильно поняли.После этого в дискуссию вступили некоторые посторонние наблюдатели, которые с некоторым недоумением заявили приблизительно следующее: «Ребята, вы молодцы, конечно, что занимаетесь столь сложным вопросом. Но, если вы правы, то ваши результаты должны повторяться у других научных групп. Чего мы в данном конкретном случае не наблюдаем». Датчане тоже не собирались отмалчиваться:»Спасибо, что прояснили нам некоторые моменты относительно своей компьютерной программы, но мы провели повторный анализ, и продолжаем считать,что полученные вами результаты некорректны».

Однородный газ произвольных размеров

Плотность состояний

Используя объемный интеграл по размерам, плотность состояний равна:
d{\ textstyle d}

грамм(d)(E)знак равнограммs∫ddk(2π)dδ(E-E-ℏ2|k|22м)знак равнограммs (м2πℏ2)d2(E-E)d2-1Γ(d2){\ displaystyle g ^ {(d)} (E) = g_ {s} \ int {\ frac {\ mathrm {d} ^ {d} \ mathbf {k}} {(2 \ pi) ^ {d}} } \ delta \ left (E-E_ {0} — {\ frac {\ hbar ^ {2} | \ mathbf {k} | ^ {2}} {2m}} \ right) = g_ {s} \ \ left ({\ frac {m} {2 \ pi \ hbar ^ {2}}} \ right) ^ {d / 2} {\ frac {(E-E_ {0}) ^ {d / 2-1}} { \ Gamma (d / 2)}}}

Энергия Ферми получается путем поиска плотности числа частиц:

ρзнак равноNVзнак равно∫EE+EF(d)грамм(d)(E)dE{\ displaystyle \ rho = {\ frac {N} {V}} = \ int _ {E_ {0}} ^ {E_ {0} + E _ {\ mathrm {F}} ^ {(d)}} g ^ {(d)} (E) \, \ mathrm {d} E}

Получить:

EF(d)знак равно2πℏ2м(1граммsΓ(d2+1)NV)2d{\ displaystyle E _ {\ mathrm {F}} ^ {(d)} = {\ frac {2 \ pi \ hbar ^ {2}} {m}} \ left ({\ tfrac {1} {g_ {s}) }} \ Gamma \ left ({\ tfrac {d} {2}} + 1 \ right) {\ frac {N} {V}} \ right) ^ {2 / d}}

где — соответствующий d -мерный объем, — размерность внутреннего гильбертова пространства. В случае спина 1/2 каждая энергия дважды вырождена, так что в этом случае .
V{\ textstyle V}граммs{\ textstyle g_ {s}}граммsзнак равно2{\ textstyle g_ {s} = 2}

Частный результат получается при , где плотность состояний становится постоянной (не зависит от энергии):
dзнак равно2{\ displaystyle d = 2}

грамм(2D)(E)знак равнограммs2мπℏ2{\ displaystyle g ^ {(2 \ mathrm {D})} (E) = {\ frac {g_ {s}} {2}} {\ frac {m} {\ pi \ hbar ^ {2}}}}.

КВА́НТОВЫЙ ГАЗ

В книжной версии

Том 13. Москва, 2009, стр. 471

Скопировать библиографическую ссылку:

КВА́НТОВЫЙ ГАЗ, газ, в ко­то­ром су­ще­ст­вен­на роль об­мен­ных взаи­мо­дей­ст­вий, обу­слов­лен­ных не­раз­ли­чи­мо­стью (то­ж­де­ст­вен­но­стью) со­став­ляю­щих его час­тиц – ато­мов, мо­ле­кул, элек­тро­нов в ме­тал­ле и др. Фи­зич. свой­ст­ва К. г. за­ви­сят от ти­па ста­ти­сти­ки, ко­то­рой под­чи­ня­ют­ся его час­ти­цы ( Бо­зе – Эйн­штей­на ста­ти­сти­ке или Фер­ми – Ди­ра­ка ста­ти­сти­ке ); в свя­зи с этим су­ще­ст­ву­ют бо­зе-га­зы и фер­ми-га­зы со­от­вет­ст­вую­щих час­тиц.

Вывод распределения[]

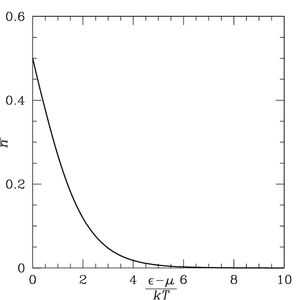
Распределение Ферми — Дирака как функция от ε. Высокоэнергетические состояния имеют меньшую вероятность. Или, низкоэнергитические состояния более вероятны

Рассмотрим состояние частицы в системе, состоящей из множества частиц. Энергия такой частицы равна ϵ{\displaystyle \mathbf {\epsilon } }. Например, если наша система — это некий квантовый газ в «ящике», то подобное состояние может описываться частной волновой функцией. Известно, что для большого канонического ансамбля, функция распределения имеет вид

Z=∑se−(E(s)−μN(s))kT{\displaystyle Z\;=\sum _{s}e^{-(E(s)-\mu N(s))/kT}}

где

E(s) {\displaystyle E(s)\ } — энергия состояния s,

N(s) {\displaystyle N(s)\ } — число частиц, находящихся в состоянии s,

μ{\displaystyle \mu } — химический потенциал,

s — это индекс, пробегающий все возмножные микросостояния системы.

В данном контексте, система имеет фиксированные состояния. Итак, если какое либо состояние занято n частицами, то энергия системы — n⋅ϵ{\displaystyle n\cdot \epsilon }. Если состояние свободно, то энергия имеет значение . Будем рассматривать равновесные одночастичные состояния как резервуар. После того, как система и резервуар займут одно и тоже физическое пространство, начинает происходить обмен частицами между двумя состояниями (фактически, это явление мы и исследуем). Отсюда становится ясно, почему используется описанная выше функция распределения, которая, через химический потенциал, учитывает поток частиц между системой и резервуаром.

Для фермионов, каждое состояние может быть либо занято одной частицей, либо свободно. Поэтому, наша система имеет два множества: занятых (разумеется, одной частицей) и незанятых состояний, обозначающихся s1{\displaystyle s_{1}} and s2{\displaystyle s_{2}} соответственно. Видно, что E(s1)=ϵ{\displaystyle E(s_{1})=\;\epsilon }, N(s1)=1{\displaystyle N(s_{1})=\;1}, и E(s2)={\displaystyle E(s_{2})=\;0}, N(s2)={\displaystyle N(s_{2})=\;0}. Поэтому функция распределения принимает вид:

Z=∑i=12e−(E(si)−μN(si))kT=e−(ϵ−μ)kT+1{\displaystyle Z=\sum _{i=1}^{2}e^{-(E(s_{i})-\mu N(s_{i}))/kT}=e^{-(\epsilon -\mu )/kT}+1}.

Для большого канонического ансамбля, вероятность того, что система находится в микросостоянии sα{\displaystyle s_{\alpha }} вычисляется по формуле

P(sα)=e−(E(sα)−μN(sα)Z{\displaystyle P(s_{\alpha })={\frac {e^{-(E(s_{\alpha })-\mu N(s_{\alpha })}}{Z}}}.

Наличие состояния, занятого частицей, означает, что система находится в микросостоянии s1{\displaystyle s_{1}}, вероятность которого

n¯=P(s1)=e−(E(s1)−μN(s1))kTZ=e−(ϵ−μ)kTe−(ϵ−μ)kT+1=1e(ϵ−μ)kT+1{\displaystyle {\bar {n}}=P(s_{1})={\frac {e^{-(E(s_{1})-\mu N(s_{1}))/kT}}{Z}}={\frac {e^{-(\epsilon -\mu )/kT}}{e^{-(\epsilon -\mu )/kT}+1}}={\frac {1}{e^{(\epsilon -\mu )/kT}+1}}}.

n¯{\displaystyle {\bar {n}}} называется распределением Ферми — Дирака. Для фиксированной температуры T, n¯(ϵ){\displaystyle {\bar {n}}(\epsilon )} есть вероятность того, что состояние с энергией ε будет занято фермионом

Обратите внимание, что
n¯{\displaystyle {\bar {n}}} является убывающей функцией от ε. Это соответствует нашим ожиданиям: высокоэнергетические состояния занимаются с меньшей вероятностью.

Обратите внимание, что энергетический уровень ε имеет вырождение gϵ{\displaystyle \;g_{\epsilon }}. Теперь можно произвести простую модификацию:

n¯=gϵ⋅1e(ϵ−μ)kT+1{\displaystyle {\bar {n}}=g_{\epsilon }\cdot {\frac {1}{e^{(\epsilon -\mu )/kT}+1}}}.

Это число — ожидаемое число частиц, в суммарном состоянии с энергией ε.

Для всех температур T, n¯(μ)=12{\displaystyle {\bar {n}}(\mu )={\frac {1}{2}}}. Это означает, что состояния с энергией μ всегда будут иметь одинаковую вероятность быть заполнеными или свободными.

В пределе T→{\displaystyle T\rightarrow 0}, n¯{\displaystyle {\bar {n}}} становится ступенчатой функцией (см. первый график). Все состояния с энергией меньше химического потенциала μ будут заняты с вероятностью 1. Состояния с энергией выше химического потенциала μ будут свободны. Химический потенциал при нулевой температуре — энергия Ферми, обозначается EF{\displaystyle E_{F}}, то есть

EF=μ(T=){\displaystyle E_{F}=\;\mu (T=0)}.