Постоянная больцмана: история, уравнения, исчисление, упражнения

Формула

Такую возможность дает нам как раз наша константа. Энергия рассчитывается по формуле:

1/2mv²=Tk

Где m – масса молекул газа, v – скорость их движения, T – результирующая температура и k – собственно, константа Больцмана. Она равняется 1,38 x 10–23 Дж/К.

Таким образом, в левой части формулы мы видим характеристики атомарного микромира – масса и скорость молекул. В правой же части получаем характеристику макромира, которую мы можем измерить доступными нам инструментами – термометром. Мостик проложен.

Немного отвлечемся от основной темы. А вы знали, что автор нашей постоянной известен своей философской концепцией Больцмановского мозга? В соответствии с ней, вероятность появления интеллекта в результате флуктуаций (то есть, случайно, мгновенно), выше, чем в результате эволюции. При условии, что время жизни Вселенной не ограничено.

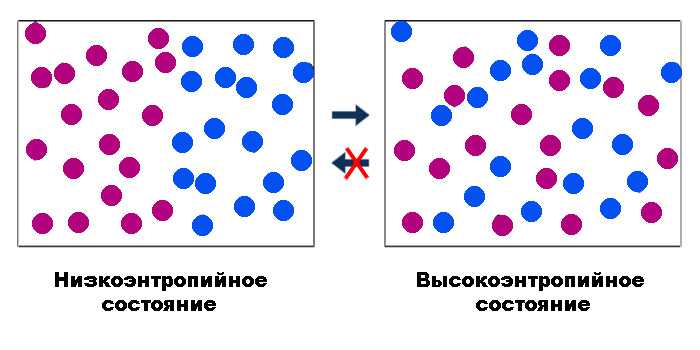
Константа k и энтропия

В общем смысле энтропию можно охарактеризовать как меру необратимости термодинамического процесса. Эта необратимость связана с рассеянием – диссипацией – энергии. При статистическом подходе, предложенном Больцманом, энтропия является функцией количества способов, которыми может быть реализована физическая система без изменения ее состояния: S = k∙lnW.

Здесь постоянная k задает масштаб роста энтропии с увеличением этого количества (W) вариантов реализации системы, или микросостояний. Макс Планк, который привел данную формулу к современному виду, и предложил дать константе k имя Больцмана.

Примеры решения задач

Пример

Задание. Две частицы летят навстречу друг другу со скоростями равными v (скорость близка к скорости света).
При их соударении происходит абсолютно неупругий удар. Какова масса частицы, которая образовалась после соударения? Массы частиц
до соударения равны m.

Решение. При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна:

$$E^{\prime}=M c^{2}(1.1)$$

В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией.
По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики:

$$E_{1}=\frac{m c^{2}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=E_{2}(1.2)$$

где E₁ – энергия первой частицы до удара, E₂ – энергия второй частицы до соударения.

Закон сохранения энергии запишем в виде:

$$E_{1}+E_{2}=E^{\prime} ; \frac{m c^{2}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}+\frac{m c^{2}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=M c^{2} \rightarrow \frac{2 m c^{2}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}=M c^{2}(1.3)$$

Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна:

$$M=\frac{2 m}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$$

Слишком сложно?

Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Какова масса 2м3 меди?

Решение. Будем считать, что медь однородна и для решения задачи используем формулу:

$$m=\rho V$$

При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$\rho$ _Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:

$m=8900 \cdot 2=17800$ (кг)

Ответ. $m=8900 \cdot 2=17800$ (кг)

Читать дальше: Формула момента силы.

Физический смысл постоянной Больцмана

Исторически
температура была впервые введена как
термодинамическая величина, и для нее
была установлена единица измерения —
градус (см. § 3.2). После установления
связи температуры со средней кинетической
энергией молекул стало очевидным, что
температуру можно определять как среднюю
кинетическую энергию молекул и выражать
ее в джоулях или эргах, т. е. вместо
величины Т
ввести
величину Т*
так,
чтобы

Определенная таким
образом температура связана с температурой,
выражаемой в градусах, следующим образом:

Поэтому постоянную
Больцмана можно рассматривать как
величину, связывающую температуру,
выражаемую в энергетических единицах,
с температурой, выраженной в градусах.

Связь с энтропией и вероятностью

Постоянная Больцмана (обозначается как k) имеет глубокую связь с энтропией и вероятностью в статистической физике. Энтропия – это мера беспорядка или неопределенности системы, а вероятность – это вероятность нахождения системы в определенном состоянии.

Энтропия и вероятность

Энтропия системы (обозначается как S) связана с вероятностью состояний системы. Чем больше вероятность состояний, тем больше энтропия системы. Если система имеет большое количество возможных состояний, то она имеет высокую энтропию. Если же система имеет мало возможных состояний, то она имеет низкую энтропию.

Вероятность состояния системы (обозначается как P) определяется отношением числа состояний, соответствующих данному состоянию, к общему числу возможных состояний системы. Чем больше число состояний, соответствующих данному состоянию, тем выше вероятность этого состояния.

Связь с постоянной Больцмана

Связь постоянной Больцмана с энтропией и вероятностью выражается следующим образом:

S = k * ln(W)

где S – энтропия системы, k – постоянная Больцмана, W – число возможных состояний системы.

Эта формула показывает, что энтропия системы пропорциональна логарифму числа возможных состояний системы. Постоянная Больцмана k является коэффициентом пропорциональности между энтропией и логарифмом числа состояний.

Таким образом, постоянная Больцмана позволяет нам связать энтропию системы с вероятностью состояний. Чем больше число возможных состояний системы, тем больше энтропия и вероятность состояний. Постоянная Больцмана играет важную роль в статистической физике, позволяя нам анализировать и предсказывать поведение системы на основе ее энтропии и вероятности состояний.

Основное соотношение температуры и энергии

Традиционная модель идеального газа активно используется для правильного расчёта состояний реального вещества при давлениях и температурах, которые близки к нормальным показателям.

В этом случае размер молекулы существенно меньше объёма, который занят определённым количеством газа. А вот расстояние между частицами существенно превышает итоговый радиус их тесного взаимодействия.

В кинетической теории чётко описаны все необходимые понятия уравнения. Для поиска средней энергии таких частиц принято использовать следующую формулу: Ecp = 3/2 * kT.

Расшифровка выглядит следующим образом:

• Т — температура.
• Е — кинетическая энергия.
• 3,2* k — используемый коэффициент пропорциональности.

В этом случае используется число 3, которое характеризует количество степеней свободы поступательного движения молекул в трёх пространственных измерениях.

А вот величину k через некоторое время назвали постоянной Больцмана в честь австрийского физика. Этот термин призван показывать то, какую часть энергии или джоуля содержит в себе один градус.

Значение константы определяет, насколько именно может статистически увеличиваться энергия хаотического движения одного фрагмента идеального газа при повышении температуры на 1°. Общая энергия теплового излучения определяется законом Стефана — Больцмана.

Как соотносится энергия и температура

При абсолютной температуре T в идеальном однородном газе на каждую поступательную степень свободы приходится энергия \(kT/2\), что следует из распределения Максвелла. Значение этой энергии при 300 К (комнатной температуре) составляет примерно

\(2.07\times10^{-21} Дж.\)

В идеальном одноатомном газе каждый атом имеет три степени свободы, которые соответствуют трем пространственным осям. Поэтому энергию, приходящуюся на каждый атом можно выразить как

\(\frac{3kT}2\)

Если известна величина тепловой энергии, то нетрудно рассчитать среднеквадратичную скорость атомов. Она будет обратно пропорциональна корню квадратному из атомной массы. Например, при температуре 300 К среднеквадратичная скорость молекул ксенона составит 240 м/с, а гелия — 1370 м/с.

Вычисления для молекулярного газа усложняются. Это связано с увеличением степеней свобод. Так, например, при низкой температуре двухатомный газ имеет уже две вращательных и три поступательных степеней свободы. Рассмотрим решение конкретной задачи.

Задача

Газ состоит из N-атомных объемных молекул и находится при определенной температуре Т, при которой у молекул возбуждены колебательные, вращательные и поступательные степени свободы. Найти среднюю энергию молекул этого газа.

Решение

На каждую степень свободы в среднем приходится одинаковая величина кинетической энергии (закон равномерного распределения энергии по степеням свободы), которая равна

\(\left\langle\Sigma_i\right\rangle=\frac{kT}2\)

Тогда можно утверждать, что средняя энергия молекулы составит

\(\left\langle\Sigma\right\rangle=\frac{ikT}2\)

Сделаем небольшое пояснение: i — сумма поступательных, вращательных и удвоенного количества колебательных степеней свободы, то есть

\(i=m_{post}+m_{vr}+2m_{kol}\)

Теперь необходимо определить сколько степеней свободы имеют молекулы рассматриваемого газа:

\(m_{post}=3, m_{vr}=3\)

тогда \(m_{kol}=3N-6\)

\(i=6+6N-12=6N-6\)

\(\left\langle\Sigma\right\rangle=\frac{6N-6}2kT\)

Сокращаем полученное выражение и получаем:

\(\left\langle\Sigma\right\rangle=\left(3N-3\right)kT\)

Лабораторная работа по физике «Определение постоянной Стефана-Больцмана»

• Вид работы: Лабораторная работа
• Предмет: Физика
• Тема: «Определение постоянной Стефана-Больцмана»

Краткое теоретическое содержание работы

Интегральной излучательной способностью R называется величина, равная количеству энергии излучаемой ежесекундно единицей поверхности тела по всем направлениям с учетом всех длин волн испускаемых телом

Спектральной излучательной способностью rλ называется величина, равная количеству энергии излучаемой ежесекундно с единицы поверхности тела по всем направлениям с длинами волн рассчитанная на единичный интервал длин волн

R_0=σT^4

где σ — постоянная Стефана-Больцмана

R=a_T σT^4

где aT — коэффициент черноты

Принцип работы пирометра с исчезающей нитью:

1. Основан на сравнении (визуальном) спектральных излучательных способностей раскаленной нити лампы пирометра и исследуемого тела при той же длине волны.
2. Оптическая схема пирометра
3. Обозначения:
4. 1 — Светофильтр
   2 — Нить лампы
   3 — Объектив
   4 — Миллиамперметр
   5 — Окуляр
5. 6 — Реостат

Нагреваемым телом служит Окись нихрома (пластинка)

Расчётные формулы

Постоянная Стефана – Больцмана:

Ответ в течение 5 минут!Без посредников!

где

• I — Сила тока
• U — Напряжение на пластинке
• αT — Коэффициент черноты данного тела
• S — Поверхность излучателя
• T — Истинная температура

где

• k — Постоянная Больцмана
• c — Скорость света в вакууме
• σ — Постоянная Стефана-Больцмана

График зависимости истинной температуры T от яркостной Tяр:

Результаты расчётов

• σ1 = (17∙1,25)/(0,95∙35∙〖10〗^(-6)∙〖1248〗^4 )=4,78∙〖10〗^(-8) (Вт/м^2∙К^4)
• σ2 = (18∙1,33)/(0,95∙35∙〖10〗^(-6)∙〖1298〗^4 )=5,09∙〖10〗^(-8) (Вт/м^2∙К^4)
• σ3 = (19∙1,39)/(0,95∙35∙〖10〗^(-6)∙〖1348〗^4 )=5,43∙〖10〗^(-8) (Вт/м^2∙К^4)
• ((4,78+5,09+5,43)∙〖10〗^(-8))/3=5,11∙〖10〗^(-8) (Вт/м^2∙К^4)
• ∛((2∙(3,14)^5∙(1,38∙〖10〗^(-23) )^4)/(15∙(3∙〖10〗^8 )^2∙5,1∙〖10〗^(-8) ))=6,864∙〖10〗^(-34) (Дж∙с)

Обработка результатов измерений

Формула относительной погрешности измерений:

• σ_сист=σ ̅∙√(((∆I/I)^2+(∆U/U)^2+(∆S/S)^2+(∆T/T)^2 ) )
• σ_сист=5,11∙〖10〗^(-8)∙√(((0,5/17)^2+(0,005/1,25)^2+((5,5∙〖10〗^(-6))/(35∙〖10〗^(-6) ))^2+((4∙0,5)/1248)^2 ) )=2,94∙〖10〗^(-9)
• σ_сл=t_(p,N) √((∑▒(σ ̅-σ_i )^2 )/(N(N-1))=) 4,3∙√((0,221∙〖10〗^(-16))/3(3-1) =8,28)∙〖10〗^(-9) (Вт/м^2∙К^4 )
  ∆σ=√((σ_сл )^2+(σ_сист )^2 )=√((8,28∙〖10〗^(-9) )^2+(2,94∙〖10〗^(-9) )^2 )=8,78∙〖10〗^(-9) (Вт/м^2∙К^4 )

где
—

Среднее значение постоянной Стефана-Больцмана

• ΔI — погрешность силы тока
• ΔU — погрешность напряжения
• ΔS — погрешность площади пластинки
• ΔT — погрешность истинной температуры

ΔS = ∆S=S∙√(((∆l/l)^2+(∆d/d)^2 ) )=35∙〖10〗^(-6)∙√(((0,05/1)^2+(0,05/35)^2 ) )=5,52 〖мм〗^2

где

• Δl — погрешность длины пластинки
• Δd — погрешность толщины пластинки

• ΔI = 0,5 А
• ΔU = 0,005 В
• Δl = 0,05 мм
• Δd = 0,05 мм
• ΔS = 5,52•10-6 м
• ΔT = 0,5 К

8,78∙〖10〗^(-9) ( Вт/м^2∙К^4 )

Определили постоянную Больцмана:

σ=(5,11±0,87)∙〖10〗^(-8) (Вт/м^2∙К^4)

А табличное значение:

σ_табл=5,67∙〖10〗^(-8) (Вт/м^2∙К^4)

Лежит в области погрешности.

И определили постоянную Планка:

h=6,864∙〖10〗^(-34) (Дж∙с)

Они практически сравнима с табличным:

Прикрепленные файлы:

Ответ в течение 5 минут!Без посредников!

reportO14

Администрация сайта не рекомендует использовать бесплатные работы для сдачи преподавателю. Эти работы могут не пройти проверку на уникальность. Узнайте стоимость уникальной работы, заполните форму ниже: Узнать стоимость

Скачать файлы:

Постоянная Больцмана

Людвиг Больцман — один из создателей молекулярно-кинетической теории газов, на которой зиждется современная картина взаимосвязи между движением атомов и молекул с одной стороны и макроскопическими свойствами материи, такими как температура и давление, с другой. В рамках такой картины давление газа обусловлено упругими ударами молекул газа о стенки сосуда, а температура — скоростью движения молекул (а точнее, их кинетической энергией).Чем быстрее движутся молекулы, тем выше температура.

Постоянная Больцмана дает возможность напрямую связать характеристики микромира с характеристиками макромира — в частности, с показаниями термометра. Вот ключевая формула, устанавливающая это соотношение:

где m и v — соответственно масса и средняя скорость движения молекул газа, Т — температура газа (по абсолютной шкале Кельвина), а k — постоянная Больцмана. Это уравнение прокладывает мостик между двумя мирами, связывая характеристики атомного уровня (в левой части) с объемными свойствами (в правой части), которые можно измерить при помощи человеческих приборов, в данном случае термометров. Эту связь обеспечивает постоянная Больцмана k, равная .

Раздел физики, изучающий связи между явлениями микромира и макромира, называется статистическая механика. В этом разделе едва ли найдется уравнение или формула, в которых не фигурировала бы постоянная Больцмана. Одно из таких соотношений было выведено самим австрийцем, и называется оно просто уравнение Больцмана:

где S — энтропия системы (см. Второе начало термодинамики), p — так называемый статистический вес (очень важный элемент статистического подхода), а b — еще одна константа.

Всю жизнь Людвиг Больцман в буквальном смысле опережал свое время, разрабатывая основы современной атомной теории строения материи, вступая в яростные споры с подавляющим консервативным большинством современного ему научного сообщества, считавшего атомы лишь условностью, удобной для расчетов, но не объектами реального мира. Когда его статистический подход не встретил ни малейшего понимания даже после появления специальной теории относительности, Больцман в минуту глубокой депрессии покончил с собой. Уравнение Больцмана высечено на его надгробном памятнике.

Австрийский физик. Родился в Вене в семье госслужащего. Учился в Венском университете на одном курсе с Йозефом Стефаном (см. Закон Стефана—Больцмана). Защитившись в 1866 году, продолжил научную карьеру, занимая в разное время профессорские должности на кафедрах физики и математики университетов Граца, Вены, Мюнхена и Лейпцига. Будучи одним из главных сторонников реальности существования атомов, сделал ряд выдающихся теоретических открытий, проливающих свет на то, каким образом явления на атомном уровне сказываются на физических свойствах и поведении материи.

Статистическое рассредотачивание

Так как макроскопические состояния материи считаются итогом поведения большого числа частиц, они описываются статистическими способами. Последнее подразумевает выяснение того, как распределяются энергосвойства молекул газа.

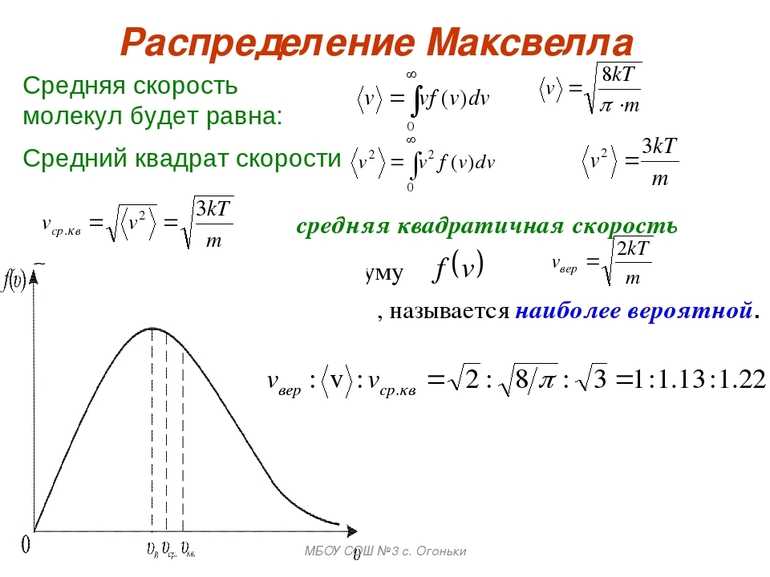
Рассредотачивание кинетических скоростей по Максвеллу происходит по-разному. Практически он показывает, что в равновесном газе главное множество молекул содержит части, более близкие к вероятным v = √ (2kT / m0), где m0-масса молекулы.

Определение Больцманом возможных энергий для газов будет пребывать на фоне всякой силы, к примеру, гравитации. Это зависит от пропорции 2-х вещей:

• притяжения к Земле;
• хаотического термического перемещения частиц газа.

Оба статистических способа связаны с рассредотачиванием Максвелла-Больцмана, содержащим экспоненциальный коэффициент eE / kT, где E — сумма кинетической и возможной энергий, а kT — средняя сила термического смещения, обусловленная ПБ. Формула постоянной Больцмана — коэффициент, равный k=1,38·10−23 ДжК.

Константа пропорциональности неизменна по Больцману. Это выражение, которое определяет связь между микроскопическим и макроскопическим состояниями, выражает центральную идею статистической механики. Планковское число измерений температуры составляет 1 416 785 (71) • 1032 К, что фактически соответствует энергии массового спокойствия.

Распределение молекул статистическим образом

Учащихся часто интересует вопрос, чему равно значение постоянной Больцмана, так как это направление имеет огромную ценность в физике.

Учёными было доказано, что состояние вещества макроскопического порядка представляет собой конкретный результат поведения огромной совокупности определённых частиц, так как именно с их помощью можно описать все существующие сегодня статистические методы.

Для решения элементарных задач обязательно нужно разобраться в том, каким именно образом происходит распределение энергетических параметров молекул газа.

В этом случае следует учесть несколько важных нюансов:

1. На практике было доказано, что физический смысл постоянной Больцмана обязательно включает в себя своеобразное максвелловское распределение кинетических скоростей и энергий. Результат в полном объёме отображает то, что когда газ пребывает в состоянии равновесия, большинство молекул обладает определёнными скоростями, близкими к некоторой наиболее вероятной скорости. Для отображения массы молекулы предназначена определённая формула: v = √(2kT/m0).
2. Практикуется применение статистики Больцмановского распределения потенциальных энергий для газов, пребывающих в поле каких-либо сил. К примеру, гравитация на нашей планете. Итоговый показатель во многом зависит от соотношения сразу двух факторов: притяжения к поверхности Земли, а также хаотического теплового движения частиц газа. Это значит, что чем ниже будет потенциальная энергия молекул, тем выше будет их итоговая концентрация.

В этом случае учёные предусмотрели наличие экспоненциального множителя — е-Е/ kT. Большой буквой Е обозначают сумму кинетической и потенциальной энергии. А вот kT обозначают среднюю энергию теплового движения, которая отлично управляется постоянной талантливого физика Больцмана.

Краткая теория и методика выполнения работы

Удельной
теплоемкостью
вещества называется величина, равная
количеству теплоты, которую необходимо
сообщить единице массы вещества для
увеличения ее температуры на один градус
Кельвина:

. (4.1)

Теплоемкость
одного моля вещества называется молярной
теплоемкостью:

, (4.2)

где
m – масса, µ – молярная масса вещества,– число молей газа.

Значение
теплоемкости газов зависит от условий
их нагревания. В соответствии с первым
законом термодинамики количество
теплоты,
сообщенное системе, расходуется на
увеличение ее внутренней энергиии на совершение системой работыпротив внешних сил:

. (4.3)

Изменение
внутренней энергии идеального газа в
случае изменения его температурыравно:

, (4.4)

здесь
– число степеней свободы молекулы газа,
под которым подразумевается число
независимых координат, полностью
определяющих положение молекулы в
пространстве;– универсальная газовая постоянная.

При
расширении газа система совершает
работу:

. (4.5)

Если
газ нагревать при постоянном объеме
(),
тои, согласно (4.3), все полученное газом
количество теплоты расходуется только
на увеличение его внутренней энергии.
Следовательно, учитывая (4.4), молярная
теплоемкость идеального газа при
постоянном объеме будет равна:

. (4.6)

Если
газ нагревать при постоянном давление
(),
то полученное газом количество теплоты
расходуется на увеличение его внутренней
энергиии совершение газом работы:

Тогда
молярная теплоемкость идеального газа
при постоянном давлении определяется
следующим образом:

. (4.7)

Используя
уравнение состояния идеального газа
(уравнение Клапейрона–Менделеева),
можно показать, что для одного моля газа
справедливо соотношение:

,

поэтому:

Последнее выражение
называют уравнением Майера. Из него,
учитывая (4.6), получаем:

. (4.8)

Отношение
теплоемкостейобозначаюти называют показателем адиабаты или
коэффициентом Пуассона:

. (4.9)

Адиабатным
называется процесс, протекающий в
термоизолированной системе, т.е. без
теплообмена с окружающей средой,.

На
практике он может быть осуществлен в
системе, окруженной теплоизоляционной
оболочкой, но поскольку для теплообмена
необходимо некоторое время, то адиабатным
можно считать также процесс, который
протекает так быстро, что система не
успевает вступить в теплообмен с
окружающей средой.

Первый
закон термодинамики для адиабатного
процесса имеет вид.
Знак минус говорит о том, что при
адиабатном процессе система может
совершать работу только за счет внутренней
энергии. С учетом (4.4)–(4.6) имеем:

. (4.10)

Продифференцировав
уравнение Клапейрона–Менделеева,
получим:

Выразим
из негои подставим в формулу (4.10):

Выразивиз уравнения Майера и учитывая соотношение
(4.8), получим:

Интегрируя
данное дифференциальное уравнение при
условииполучим выражение:

.
(4.11)

Уравнение
(4.11) называется уравнением адиабаты или
уравнением Пуассона.

Метод
определения показателя адиабаты,
предложенный Клеманом и Дезормом (1819
г.), основывается на изучении параметров
некоторой массы газа, переходящей из
одного состояния в другое двумя
последовательными процессами –
адиабатным и изохорным. Эти процессы
на диаграмме–(рис. 4.1) изображены кривыми соответственно
1–2 и 2–3.

Если
в сосуд, соединенный с дифференциальным
датчиком давления, накачать воздух и
подождать до установления теплового
равновесия с окружающей средой, то в
этом начальном состоянии 1 газ имеет
параметры,,,
причем температура газа в сосуде равна
температуре окружающей среды,
а давлениенемного больше атмосферного.

Если
теперь на короткое время соединить
сосуд с атмосферой, то произойдет
адиабатное расширение воздуха. При этом
воздух в сосуде перейдет в состояние
2, его давление понизится до атмосферного.
Масса воздуха, оставшегося в сосуде,
которая в состоянии 1 занимала часть
объема сосуда, расширяясь, займет весь
объем.
При этом температура воздуха, оставшегося
в сосуде, понизится до.
Поскольку процесс 1–2 – адиабатный, к
нему можно применить уравнение Пуассона
(4.11):

или.

Отсюда:

. (4.12)

После
кратковременного соединения сосуда с
атмосферой охлажденный из-за адиабатного
расширения воздух в сосуде будет
нагреваться (процесс 2–3) до температуры
окружающей средыпри постоянном объеме.
При этом давление в сосуде поднимется
до.

Поскольку
процесс 2–3 – изохорный, к нему можно
применить закон Шарля:

или

. (4.13)

Из уравнений (4.12)
и (4.13) получим:

Прологарифмируем
это выражение:

Поскольку
избыточные давленияиочень малы по сравнению с атмосферным
давлением,
а также учитывая, что при,
будем иметь:

Откуда:

. (4.14)

Избыточные
давленияиизмеряют с помощью дифференциального
датчика давления.

Зависимость давления газа от концентрации его молекул и температуры

ВыразивЕиз
соотношения (4.5.5) и подставив в формулу
(4.4.10), получим выражение, показывающее
зависимость давления газа от концентрации
молекул и температуры:

(4.5.6)

Из формулы (4.5.6)
вытекает, что при одинаковых давлениях
и температурах концентрация молекул у
всех газов одна и та же.

Отсюда следует
закон Авогадро: в равных объемах газов
при одинаковых температурах и давлениях
содержится одинаковое число молекул.

Средняякинетическая энергия поступательного
движения молекул прямо пропорциональна
абсолютной температуре. Коэффициент
пропорциональности—постоянную
Больцманаk=
10 -23 Дж/К
— надо
запомнить.

История

Постоянная Больцмана названа в честь ее 19 века. Австрийский первооткрыватель Людвиг Больцман. Хотя Больцман впервые связал энтропию и вероятность в 1877 году, это отношение никогда не выражалось конкретной константой до тех пор, пока Макс Планк впервые не ввел k и не дал для него точное значение (1,346 × 10 Дж / K, около 2,5% ниже, чем сегодняшняя цифра), в его выводе закона излучения черного тела в 1900–1901 гг. До 1900 года уравнения, включающие факторы Больцмана, писались не с использованием энергии на молекулу и постоянной Больцмана, а с использованием формы газовой постоянной R и макроскопических энергий для макроскопических количеств вещества. Иконическая лаконичная форма уравнения S = k ln W на надгробии Больцмана на самом деле принадлежит Планку, а не Больцману. Планк фактически представил ее в той же работе, что и его одноименный h.

. В 1920 году Планк написал в своей нобелевской лекции :

Эту постоянную часто называют постоянной Больцмана, хотя насколько мне известно, сам Больцман никогда не вводил этого — особенное положение дел, которое можно объяснить тем фактом, что Больцман, как видно из его периодических высказываний, никогда не думал о возможности проведения точного измерения постоянной <.>Это «своеобразное положение дел» иллюстрируется ссылкой на одну из великих научных дискуссий того времени. Во второй половине девятнадцатого века существовало значительное разногласие относительно того, были ли атомы и молекулы реальными или они были просто эвристическим инструментом для решения проблем. Не было согласия относительно того, являются ли химические молекулы, измеренные с помощью атомной массы, такими же, как физические молекулы, измеренные с помощью кинетической теории. Лекция Планка 1920 года продолжалась:

Ничто не может лучше проиллюстрировать позитивный и лихорадочный темп прогресса, достигнутого искусством экспериментаторов за последние двадцать лет, чем тот факт, что с тех пор не только один, но и огромное количество методов были открыты для измерения массы молекулы с практически той же точностью, что и для планеты.

В версиях СИ до 2019 переопределения основных единиц СИ постоянная Больцмана была измеренная величина, а не фиксированное значение. Его точное определение также менялось на протяжении многих лет из-за переопределения кельвина (см. ) и других основных единиц СИ (см. ).

В 2017 году наиболее точные измерения постоянной Больцмана были получены с помощью акустической газовой термометрии, которая определяет скорость звука одноатомного газа в трехосной эллипсоидной камере с использованием микроволнового и акустического резонансов. Эти десятилетние усилия были предприняты с использованием различных методов в нескольких лабораториях; это один из краеугольных камней нового определения основных единиц СИ в 2019 году. Основываясь на этих измерениях, CODATA рекомендовал 1,380 649 × 10 Дж⋅К в качестве окончательного фиксированного значения постоянной Больцмана для использования в Международной системе единиц.

Формула Больцмана барометрическая

В поле тяготения Земли точное решение уравнения Больцмана показывает:

(16)

где n=
плотность у поверхности Земли, 1/м3; g
– ускорение силы тяжести, м/с2; h –
высота, м. Формула (16) является точным решением кинетического уравнения
Больцман либо в безграничном пространстве, либо при наличии границ, не
нарушающих этого распределения, при этом температура также должна оставаться
постоянной.

Эта страница оформлена Пузиной Ю.Ю. при поддержке Российского Фонда Фундаментальных
Исследований – проект №08-08-00638.

Следующая страница: Философия молекулярно-кинетического подхода

Главная   • Больцманиада   • Именные достижения

Значение постоянной Больцмана

Значение изучаемого коэффициента состоит в том, что с его помощью можно связать параметры микромира с теми параметрами, что описывают макромир, например, термодинамическую температуру с энергией поступательного движения молекул:

» open=» E = 3 2 k T .

Этот коэффициент входит в уравнения средней энергии молекулы, состояния идеального газа, кинетической теории газа, распределение Больцмана-Максвелла и многие другие. Также постоянная Больцмана необходима для того, чтобы определить энтропию. Она играет важную роль при изучении полупроводников, например, в уравнении, описывающем зависимость электропроводности от температуры.

Условие: вычислите среднюю энергию молекулы газа, состоящего из N -атомных молекул при температуре T , зная, что у молекул возбуждены все степени свободы – вращательные, поступательные, колебательные. Все молекулы считать объемными.

Энергия равномерно распределяется по степеням свободы на каждую ее степень, значит, на эти степени будет приходиться одинаковая кинетическая энергия. Она будет равна » open=» ε i = 1 2 k T . Тогда для вычисления средней энергии мы можем использовать формулу:

» open=» ε = i 2 k T , где i = m p o s t + m υ r + 2 m k o l представляет собой сумму поступательных вращательных степеней свободы. Буквой k обозначена постоянная Больцмана.

Переходим к определению количества степеней свободы молекулы:

m p o s t = 3 , m υ r = 3 , значит, m k o l = 3 N — 6 .

i = 6 + 6 N — 12 = 6 N — 6 ; » open=» ε = 6 N — 6 2 k T = 3 N — 3 k T .

Ответ: при данных условиях средняя энергия молекулы будет равна » open=» ε = 3 N — 3 k T .

Условие: есть смесь двух идеальных газов, плотность которых в нормальных условиях равна p. Определите, какова будет концентрация одного газа в смеси при условии, что мы знаем молярные массы обоих газов μ 1 , μ 2 .

Сначала вычислим общую массу смеси.

m = ρ V = N 1 m 01 + N 2 m 02 = n 1 V m 01 + n 2 V m 02 → ρ = n 1 m 01 + n 2 m 02 .

Параметр m 01 обозначает массу молекулы одного газа, m 02 – массу молекулы другого, n 2 – концентрацию молекул одного газа, n 2 – концентрацию второго. Плотность смеси равна ρ .

Теперь из данного уравнения выразим концентрацию первого газа:

n 1 = ρ — n 2 m 02 m 01 ; n 2 = n — n 1 → n 1 = ρ — ( n — n 1 ) m 02 m 01 → n 1 = ρ — n m 02 + n 1 m 02 m 01 → n 1 m 01 — n 1 m 02 = ρ — n m 02 → n 1 ( m 01 — m 02 ) = ρ — n m 02 .

Далее нам потребуется уравнение, описывающее состояние идеального газа:

p = n k T → n = p k T .

Подставим полученное равнее значение:

n 1 ( m 01 — m 02 ) = ρ — p k T m 02 → n 1 = ρ — p k T m 02 ( m 01 — m 02 ) .

Поскольку молярные массы газов нам известны, мы можем найти массы молекул первого и второго газа:

m 01 = μ 1 N A , m 02 = μ 2 N A .

Также мы знаем, что смесь газов находится в нормальных условиях, т.е. давление равно 1 а т м , а температура 290 К . Значит, мы можем считать задачу решенной.

Ответ: в данных условиях рассчитать концентрацию одного из газов можно как n 1 = ρ — p k T m 02 ( m 01 — m 02 ) , где m 01 = μ 1 N A , m 02 = μ 2 N A .

Немного истории

На рубеже 19 и 20 веков в научной среде преобладали две когорты физиков с противоположными взглядами – атомисты и антиатомисты. Первые в фундаментальных расчетах исходили из того, что все сущее состоит из атомов. Вторые считали, что атомы – суть удобные математические абстракции (как сейчас мы говорим о кварках и виртуальных частицах).

Людвиг Больцман положил начало статистической механике, внес огромный вклад в термодинамику и прояснил понятие энтропии. В своих идеях он был ярым атомистом и использовал это в построении своих научных теорий. Антиатомисты постоянно набрасывались на его идеи, а каждая новая концепция высмеивалась. Кто такое выдержит? Результатом стала тяжелая болезнь, депрессия и суицид великого ученого.