Что такое вырожденный газ и как он влияет на свойства вещества

10.5. Энергия Ферми. Критерий вырождения электронного газа

В предыдущих
рассуждениях считалось, что энергетическое положение уровня Ферми задано.
Рассмотрим, как можно найти значение энергии Ферми, если задана концентрация
свободных носителей n, p
и температура T.

Для
собственного полупроводника уравнение электронейтральности приобретает вид p – n =0 или p = n. Если ширина запрещенной зоны полупроводника
достаточно велика (E_g много больше k_BT) и если эффективные массы электронов m_n
и дырок m_p одного порядка, то уровень Ферми
будет достаточно удален от краев зон (E_C– F >2k_BT и F – E_V>2k_BT), и полупроводник будет невырожденным.

Приравнивая
значения концентраций электронов и дырок из соотношений (10.15) и (10.18),
получаем

(10.27)

Отсюда
вычисляем значение энергии Ферми F. Уравнение (10.27) – уравнение
первого порядка относительно . Решение уравнения (10.27) дает выражение для энергии Ферми

(10.28)

где через обозначена энергия
середины запрещенной зоны. При выводе в правом
выражении для энергии Ферми Fотношение
эффективных плотностей состояний (N_C/N_V) была заменена на
отношение эффективных масс (m_n/m_p) с использованием
уравнения (10.16).

Для случая m_n*= m_p*энергия
Ферми в собственном полупроводнике находится посреди запрещенной зоны

(10.29)

Если известны
концентрации носителей заряда n и p в зонах,
то значение энергии Ферми F можно определить из
формул (10.15) и (10.18). Так, для невырожденного
полупроводника n‑типа имеем:

(10.30)

Аналогично для
невырожденного полупроводника p‑типа

(10.31)

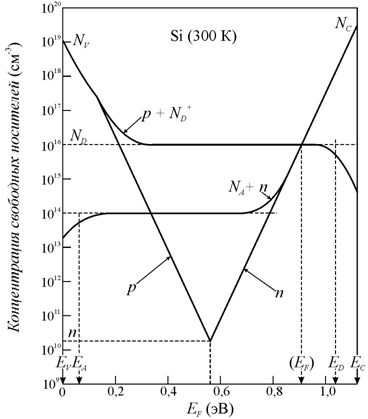
Из выражений (10.30,
10.31) видно, что чем больше концентрация основных носителей, тем ближе уровень
Ферми к краю соответствующей зоны (рис. 10.12). Для донорного полупроводника в
случае полной ионизации примеси концентрация электронов равна концентрации
донорной примеси n= N_D.
Тогда

(10.32)

Для
акцепторного полупроводника концентрация дырок равна концентрации акцепторной
примеси p= N_A(10.24), тогда

(10.33)

Рис. 10.12.
Зависимость энергии Ферми F от концентрации
свободных носителей в кремнии

Как
уже отмечалось, вырожденный и невырожденный электронный газ описывается
соответственно статистикой Ферми−Дирака и Больцмана. Квантовая статистика
переходит в классическую, если энергия состояния:. Следовательно,вырождение в полупроводнике наступает тогда, когда энергия Ферми F приближается к дну зоны проводимости или
к потолку валентной зоны на расстояние порядка k_ВT, т. е. для полупроводника p-типа: F–E_V= k_ВТ. В случае полной ионизации
примеси в акцепторном полупроводнике концентрация дырок p определяется как

(10.34)

Отсюда следует
критерий вырождения электронного газа: по мере роста концентрации свободных
носителей (по мере роста легирующей примеси) полупроводник становится
вырожденным, если концентрация свободных носителей сравняется с эффективной
плотностью состояний. Более точно, с учетом соотношения E– , получаем для
критерия вырождения N_A=p=N_V/2,73.
Используя для классических полупроводников кремния и германия табличные
значения эффективной плотности состояний, получаем количественную оценку
концентрации свободных носителей, после которых наступает вырождение: для Si p=3,8·1018см-3,
для Ge p=2,2·1018см-3.

В металлах
энергия Ферми находится внутри зоны проводимости, поэтому электронный газ в
металлах всегда вырожден. Ниже, в табл. 10.1, показано значение энергии Ферми и
волнового вектора, соответствующего энергии Ферми, для некоторых металлов .

Таблица
10.1

Энергия Ферми и волновой вектор,
соответствующий этой энергии для простых металлов

Металл	F (эВ)	k (108/см)	Металл	F (эВ)	k (108/см)
Li	4,74	1,12	Fe	11,1	1,71
Na	3,24	0,92	Mn	10,9	1,70
K	2,12	0,75	Zn	9,47	1,58
Rb	1,85	0,70	Cd	7,47	8,68
Cs	1,59	0,65	Hg	7,13	1,37
Cu	7,00	1,36	Al	11,7	1,75
Ag	5,49	1,20	Ga	10,4	1,66
Au	5,53	1,21	In	8,63	1,51
Be	14,3	1,94	Tl	8,15	1,46
Mg	7,08	1,36	Sn	10,2	1,64
Ca	4,69	1,11	Pb	9,47	1,58
Sr	3,93	1,02	Bi	9,9	1,61
Ba	3,64	0,98	Sb	10,9	1,70
Nb	5,32	1,18

Эти значения
являются полезными для практических случаев, поскольку энергия Ферми определяет
термодинамическую работу выхода, а волновой вектор определяет энергетическое
положение уровня Ферми относительно дна разрешенной зоны энергий.

Струнные сети

Каким состоянием вещества является космический вакуум? Большинство людей не задумываются об этом, но в последние десять лет Сяо Ган-Вэнь из Массачусетского технологического института и Майкл Левин из Гарварда предложили новое состояние вещества, которое могло бы привести нас к открытию фундаментальных частиц после электрона.

Путь к разработке модели струнно-сетевой жидкости начался в середине 90-х годов, когда группа ученых предложила так называемые квазичастицы, которые, казалось, появились в эксперименте, когда электроны проходили между двумя полупроводниками. Возник переполох, поскольку квазичастицы действовали так, будто бы обладали дробным зарядом, что казалось невозможным для физики того времени. Ученые проанализировали данные и предположили, что электрон является не фундаментальной частицей Вселенной и что существуют фундаментальные частицы, которых мы пока не обнаружили. Эта работа принесла им Нобелевскую премию, но позже выяснилось, что в результаты их работы закралась ошибка в эксперименте. О квазичастицах благополучно забыли.

Но не все. Вэнь и Левин взяли за основу идею квазичастиц и предложили новое состояние вещества, струнно-сетевое. Основным свойством такого состояния является квантовая запутанность. Как и в случае с неупорядоченной сверходнородностью, если вы с близкого расстояния взглянете на струнно-сетевое вещество, оно будет похоже на неупорядоченный набор электронов. Но если взглянуть на него как на цельную структуру, вы увидите высокую упорядоченность из-за квантово-запутанных свойств электронов. Вэнь и Левин затем расширили свою работу, чтобы охватить другие частицы и свойства запутанности.

Проработав компьютерные модели для нового состояния вещества, Вэнь и Левин обнаружили, что концы струн-сетей могут производить разнообразные субатомные частицы, включая легендарные «квазичастицы». Еще большим сюрпризом стало то, что при вибрации струнно-сетевого вещества оно делает это в соответствии с уравнениями Максвелла, отвечающими за свет. Вэнь и Левин предположили, что космос наполнен струнными сетями запутанных субатомных частиц и что концы этих струн-сетей представляют собой субатомные частицы, которые мы наблюдаем. Также они предположили, что струнно-сетевая жидкость может обеспечивать существование света. Если космический вакуум заполнен струнно-сетевой жидкостью, это может позволить нам объединить свет и материю.

Все это может показаться очень надуманным, но в 1972 году (за десятки лет до струнно-сетевых предложений) геологи обнаружили в Чили странный материал — гербертсмитит. В этом минерале электроны образуют треугольные структуры, которые, похоже, противоречат всему, что мы знаем о взаимодействии электронов друг с другом. Кроме того, эта треугольная структура была предсказана в рамках струнно-сетевой модели, и ученые работали с искусственным гербертсмититом, чтобы точно подтвердить модель.

Основные свойства вырожденного газа

Вырожденный газ — это особая форма газа, при которой его частицы подвергаются сильному влиянию квантовых эффектов и высоким давлениям. Этот тип газа возникает при очень низких температурах, близких к абсолютному нулю, и может наблюдаться в экстремальных условиях, таких как внутри планет или при крайних давлениях в лабораторных условиях.

Основными свойствами вырожденного газа являются:

Природа частиц. Вырожденный газ состоит из частиц, которые имеют спин и нарушают классические правила поведения частиц при высоких температурах. Квантовые эффекты становятся доминирующими, и частицы не могут занимать одни и те же энергетические уровни.
Статистика. Для описания таких газов используются квантово-механические статистические модели, такие как ферми-дираковская или бозе-эйнштейновская статистика, в зависимости от свойств частиц этого газа.
Высокие давления. Вырожденный газ обладает очень высокими давлениями, связанными с близким расположением частиц на квантово-механических уровнях. Это приводит к возникновению аномальных свойств, таких как сжатие или упругость.
Эффекты налетающих частиц. Квантовое состояние частиц в вырожденном газе влияет на их взаимодействие с другими частицами, а также на их взаимодействие с внешней средой. Например, электрически заряженные частицы будут испытывать сильное взаимодействие с электромагнитными полями.

Вырожденные газы являются объектом многих исследований и применяются в различных областях науки, таких как физика высоких энергий, астрофизика, квантовая механика и другие.

Определение «Вырожденный газ» в Большой Советской Энциклопедии

Вырожденный газ, газ, свойства которого существенно отличаются от свойств классического идеального газа вследствие квантовомеханического влияния одинаковых частиц друг на друга. Это взаимное влияние частиц обусловлено не силовыми взаимодействиями, отсутствующими у идеального газа, а тождественностью (неразличимостью) одинаковых частиц в квантовой механике (см. Тождественности принцип). В результате такого влияния заполнение частицами возможных уровней энергии даже в идеальном газе зависит от наличия на данном уровне других частиц. Поэтому теплоёмкость и давление такого газа иначе зависят от температуры, чем у идеального классического газа; по-другому выражается энтропия, свободная энергия и т. д.Вырождение газа наступает при понижении его температуры до некоторого значения, называемого температурой вырождения. Полное вырождение соответствует абсолютному нулю температуры.

Влияние тождественности частиц сказывается тем существеннее, чем меньше среднее расстояние между частицами r по сравнению с длиной волны де Бройля частиц l = h/mv (m — масса частицы, v — её скорость, h — Планка постоянная). Это объясняется тем, что классическая механика применима к движению частиц газа лишь при условии r >> l. Так как скорость частиц газа связана с температурой (чем больше скорость, тем выше температура), то температура вырождения, определяющая границу применимости классической теории, тем выше, чем меньше масса частиц газа и чем больше его плотность (т. е. чем меньше среднее расстояние между частицами). Поэтому температура вырождения особенно велика (порядка 10 000 К) для электронного газа в металлах: масса электронов очень мала (~ 10-27г), а их плотность в металлах очень велика (1022 электронов в 1 см3). Электронный газ в металлах вырожден при всех температурах, при которых металл остаётся в твёрдом состоянии.

Для обычных атомных и молекулярных газов температура вырождения близка к абсолютному нулю, так что такой газ практически всегда ведёт себя как классический (при таких низких температурах все вещества находятся в твёрдом состоянии, кроме гелия, являющегося квантовой жидкостью при сколь угодно близких к абсолютному нулю температурах).

Поскольку характер несилового влияния тождественных частиц друг на друга различен для частиц с целым (бозоны) и полуцелым (фермионы) спином, то поведение газа из фермионов (ферми-газа) и из бозонов (бозе-газа) также будет различным при вырождении.

У ферми-газа (к которому относится электронный газ в металле) при полном вырождении (при Т = 0 К) заполнены все нижние энергетические уровни вплоть до некоторого максимального, называемого уровнем Ферми, а все последующие остаются пустыми. Повышение температуры лишь незначительно изменяет такое распределение электронов металла по уровням: малая доля электронов, находящихся на уровнях, близких к уровню Ферми, переходит на пустые уровни с большей энергией, освобождая таким образом уровни ниже фермиевского, с которых был совершен переход.

При вырождении газа бозонов из частиц с отличной от нуля массой (такими бозонами могут быть атомы и молекулы) некоторая доля частиц системы должна переходить в состояние с нулевым импульсом; это явление называется Бозе — Эйнштейна конденсацией. Чем ближе температура к абсолютному нулю, тем больше частиц должно оказаться в этом состоянии. Однако, как уже говорилось, системы таких частиц при понижении температуры до очень низких значений переходят в твёрдое или жидкое (для гелия) состояния, в которых значительны силовые взаимодействия между частицами и к которым поэтому неприменимо приближение идеального газа. Явление Бозе — Эйнштейна конденсации в жидком гелии, который можно рассматривать как неидеальный газ из так называемых квазичастиц, приводит к появлению сверхтекучести.

Для газа из бозонов нулевой массы, к которым относятся фотоны (спин 1), температура вырождения равна бесконечности; поэтому фотонный газ — всегда вырожденный и классическая статистика к нему не применима ни при каких условиях. Фотонный газ является единственным вырожденным идеальным бозе-газом стабильных частиц. Однако Бозе — Эйнштейна конденсации в нём не происходит, так как не существует фотонов с нулевым импульсом (фотоны всегда движутся со скоростью света). При нулевой абсолютной температуре фотонный газ перестаёт существовать.

См. также Статистическая физика, Металлы, Полупроводники и лит. при этих статьях. Г. Я. Мякишев.

«БСЭ» >>

«В»
>>

«ВЫ»
>>

«ВЫР»

Применение вырожденного газа в науке и технике

Вырожденный газ — это состояние газа, при котором его температура находится так близко к абсолютному нулю, что квантовые эффекты начинают играть определенную роль. Такое состояние газа проявляется в особых свойствах, которые находят применение в различных областях науки и техники.

Одно из основных применений вырожденного газа — в науке, в частности в области квантовой механики и физики низких температур. Вырожденные газы могут служить объектами исследования для изучения квантовых явлений и создания устройств, работающих на основе квантовых эффектов. Так, например, бозе-эйнштейновский конденсат – это особое состояние вырожденного газа, которое позволяет исследовать поведение квантовых частиц при крайне низких температурах.

В технике вырожденный газ нашел применение, в частности, в создании лазеров и криогенной техники. Лазеры на базе вырожденных газов обладают высокой эффективностью и способны создавать мощное излучение в узком диапазоне частот. Криогенная техника использует вырожденные газы для создания экстремально низких температур, которые необходимы для работы некоторых приборов и электронных компонентов.

Применение вырожденного газа также можно встретить в сфере искусственного интеллекта. Квантовые вычисления построены на основе принципов квантовой механики, и вырожденные газы играют важную роль в создании устройств, способных решать сложные задачи, с которыми стандартные компьютеры не справляются.

Теория

Конденсат Бозе-Эйнштейна (КБЭ) на основе фотонов — это весьма «продвинутый» вариант КБЭ, и очень долго считалось, что его нельзя получить в принципе. Но прежде чем рассказать о нем, стоит пояснить, а что вообще такое конденсат Бозе-Эйнштейна. Родиной этого понятия может считаться Индия – именно там большую часть времени жил и работал человек, впервые указавший на возможность существования неизвестного ранее состояния материи. Этого человека звали Шатьендранат Бозе, и он был одним из отцов-основателей квантовой механики.

Чтобы отметить научные заслуги Бозе, в его честь был назван один из типов элементарных частиц – бозоны. К бозонам относятся, например, фотоны — переносчики электромагнетизма, и глюоны, которые переносят сильное взаимодействие и определяют притяжение друг к другу кварков. Знаменитый бозон Хиггса, ради поисков которого был создан Большой адронный коллайдер, тоже относится к этой категории элементарных частиц.

Принадлежность частицы к бозонам определяется по ее спину – собственному моменту импульса элементарных частиц (иногда понятие спина определяют как вращение частицы вокруг собственной оси, но такое представление слишком упрощает ситуацию). Спин бозона всегда целый — то есть выражается целым числом. У другой разновидности элементарных частиц — фермионов — спин полуцелый.

Фермионы (слева) выстраиваются «в линейку» по энергиям квантовых уровней, а бозоны (справа) могут скапливаться на уровне с наименьшей энергией. Изображение выпуска 23 бюллетеня ПерсТ за 2003 год

Lenta.ru

Бозоны и фермионы отличаются друг от друга не только значением спина — эти частицы несходны по целому ряду фундаментальных свойств. В частности, бозоны могут не подчиняться так называемому принципу, или запрету, Паули, который постулирует, что две элементарные частицы не могут находиться в одном и том же квантовом состоянии. Квантовые состояния отличаются друг от друга по энергиям, и при низких температурах фермионы (которые строго соблюдают запрет Паули) поочередно заполняют последовательные состояния. Первыми занимаются состояния с наименьшей энергией (самые «ненапряжные» для частиц), а последними – с самой высокой энергией. Нагляднее всего это свойство фермионов выстраиваться в линейку по квантовым состояниям заметно при низких температурах, когда поведение системы не маскируется за счет температурных флуктуаций.

Бозоны при низких температурах ведут себя иначе — они не ограничены запретом Паули и поэтому стремятся по возможности занять самые удобные места, то есть квантовые уровни с наименьшей энергией. В итоге при охлаждении бозонов происходит следующее: они начинают двигаться очень медленно — со скоростями порядка нескольких миллиметров в секунду, очень тесно «прижимаются» друг к другу, «соскакивают» в одно и то же квантовое состояние и в конце концов начинают вести себя скоординировано — так, как вела бы себя одна гигантская квантовая частица.

Именно о такой трансформации, которая должна происходить с бозонами при температурах, близких к абсолютному нулю, Шатьендранат Бозе написал в начале 1920-х годов Альберту Эйнштейну. Бозе собирался послать свои выкладки в журнал Zeitschrift fur Physik, но Эйнштейн так вдохновился идеями индийского коллеги, что немедленно сам перевел его статью с английского на немецкий и отправил в редакцию. Создатель общей и специальной теорий относительности развил соображения Бозе (индус рассматривал только фотоны, а Эйнштейн дополнил теорию Бозе для частиц, обладающих массой) и изложил свои выводы еще в двух статьях, которые также были опубликованы в Zeitschrift fur Physik.

Роль вырожденного газа в квантовой механике

Вырожденный газ — это газ, состояние которого подчиняется эффектам квантовой механики, таким как полное и частичное занятие квантовых состояний. В квантовой механике каждому квантовому состоянию газа соответствует определенное энергетическое уровень, а электроны, фермионы и бозоны располагаются в этих состояниях в соответствии с принципом выгодности.

Квантовая механика описывает свойства вырожденного газа, основываясь на принципе исключения Паули. Согласно этому принципу, два фермиона, такие как электрон или протон, не могут занимать одно и то же квантовое состояние одновременно. Это приводит к особой статистике распределения частиц, которая называется статистикой Ферми-Дирака. В результате, квантовые состояния электронов в вырожденном газе могут быть заполнены только до определенного предела, называемого уровнем Ферми.

Роль вырожденного газа в квантовой механике состоит в том, что он позволяет описать эффекты, которые играют важную роль в физике твердого тела и астрофизике. Например, электроны в металлах образуют вырожденный газ, который обладает свойствами, влияющими на их электрическую проводимость. Также вырожденные газы используются для моделирования взаимодействия между электронами в звездах и нейтронных звездах.

Важный аспект вырожденного газа в квантовой механике заключается в том, что он позволяет описать поведение системы частиц при очень низких температурах, близких к абсолютному нулю. При таких температурах, эффекты квантовой механики становятся доминирующими, и квантовые состояния начинают играть ключевую роль. Это позволяет исследовать и понять фундаментальные свойства материи и явления, которые мы можем наблюдать в макроскопическом мире.

Идеальный квантовый газ

Условием идеальности квантового газа является условие невзаимодействия между собой частиц, из которого он состоит. Благодаря отсутствию взаимодействия можно считать, что заполнение того или иного квантового состояния системы не влияет на заполнение других состояний. В общем случае, если между частицами есть, например, кулоновское взаимодействие, то, чтобы приближение идеального газа давало хорошие результаты, необходимо считать его слабым. Это приводит к условию разрежённости \displaystyle{ Na^3 \ll 1 }, где \displaystyle{ a } — длина рассеяния частиц или, что то же самое, \displaystyle{ kT \ll \frac{\hbar^2}{ma^2} }. Следовательно, полагаться, что при \displaystyle{ T \gg T_0 }, где \displaystyle{ T_0 } — температура вырождения, свойства квантового газа во многом не зависят от статистики составляющих его частиц и могут описываться статистикой Максвелла — Больцмана. Также, так как нет возможности точно регулировать число частиц в системе, имеет смысл работать в терминах большого канонического ансамбля.

Тогда, в силу независимости состояний, статсумма идеального Бозе-Ферми газа задаётся формулой \displaystyle{ \Sigma =\prod _{\alpha} \Sigma _{\alpha}, } где \displaystyle{ \Sigma_{\alpha} =(1 \pm e^{-(\varepsilon _{\alpha }-\mu)/(kT)})^{\mp 1} } — статсумма одноуровневой системы, суммирование происходит по всем уровням системы, верхние знаки соответствуют случаю Ферми-, нижние — Бозе-газа, \displaystyle{ \varepsilon _{\alpha } } — одночастичный гамильтониан, \displaystyle{ \mu } — химический потенциал газа.

Соответствующий этой статсумме большой термодинамический потенциал идеального квантового газа:

\displaystyle{ \Omega =-kT\ln(\Sigma)=-AV\int \frac{d\varepsilon \quad \varepsilon ^{3/2}}{e^{(\varepsilon -\mu)/(kT)}\pm 1},\qquad A=\frac {2^{7/2}\pi m^{3/2}g}{3h^3} },

где \displaystyle{ V } — объём системы, \displaystyle{ h } — постоянная Планка, \displaystyle{ g=2s+1 } — вырождение по спину.

Среднее число частиц на уровне: \displaystyle{ \lt N_{\alpha}\gt =\frac{1}{e^{(\varepsilon _{\alpha }-\mu)/(kT)}\pm 1} }.

Можно ещё больше унифицировать выражение для термодинамического потенциала, если заметить, что подынтегральная функция в случаях Ферми- и Бозе-газа отличается только знаком. Далее следует вынести из под интеграла все размерные параметры. Тогда термодинамический потенциал запишется в виде:

\displaystyle{ \Omega =-\overline AV(kT)^{5/2}{G}_{3/2}({\mu}/{(kT)}),\qquad \overline A=A\Gamma (5/2). },

где была введена функция
\displaystyle{ {G}_{k}(x) = \begin{cases}
{F_{k}(x)}, Fermi-Dirac \\
\zeta _{k+1}(e^x), Bose-Einstein
\end{cases} },

С обозначениями:

Для Ферми-газа функция Ферми-Дирака: \displaystyle{ F_k(\eta )=\frac 1{\Gamma (k+1)}\int_0^{\infty }\frac {dx\quad x^k}{e^{x-\eta }+1} }.
Для Бозе-газа обобщенная \displaystyle{ \zeta }-функция Римана: \displaystyle{ \zeta _k(a)=\sum _{n=1}^{\infty }\frac{a^n}{n^k}=\frac 1{\Gamma (k)}\int _0^{\infty }\frac {dx\quad x^{k-1}}{e^x/a-1} }.

Тогда, используя простое соотношение \displaystyle{ \partial_{\eta}G_k(\eta)=G_{k-1}(\eta) } и , можно получить различные термодинамические характеристики в общем виде:

Концентрация	\displaystyle{ n=-\frac{1}{V}\Biggr (\frac {\partial \Omega }{\partial \mu}\Biggl )_{T,V} }	\displaystyle{ \overline A(kT)^{3/2}{G}_{1/2}({\mu}/{(kT)}) }	Энтропия	\displaystyle{ S(T,V,\mu )=-\Biggr (\frac {\partial \Omega}{\partial T}\Biggl )_{V,\mu } }	\displaystyle{ \overline AVk^{5/2}\Bigg\{\frac 52T^{3/2}{G}_{3/2}({\mu}/{(kT)})-\frac {\mu }kT^{1/2}{G}_{1/2}({\mu}/{(kT)})\Bigg\}. }
Давление	\displaystyle{ p=-\Biggr (\frac {\partial \Omega }{\partial V}\Biggl )_{T,\mu } }	\displaystyle{ \overline A(kT)^{5/2}{G}_{3/2}({\mu}/{(kT)}) }	Теплоёмкость	\displaystyle{ C_{V,N}=T\Biggr (\frac {\partial S }{\partial T}\Biggl )_{V,N} }	\displaystyle{ \overline AVk^{5/2}T^{3/2}\Bigg\{\frac{15}4{G}_{3/2}({\mu}/{(kT)})-\frac 94\frac {{G}^{2}_{1/2}({\mu}/{(kT)})}{{G}_{-1/2}({\mu}/{(kT)})}\Bigg\}. }