Дошкольное образовательное учреждение это

Прием в дошкольные учреждения и льготы

С 2009 года детские сады не могут принимать детей самостоятельно, для этого формируются специальные комиссии по комплектованию ДОУ. Это правило не касается частных детских садов. Для приема в ДОУ родителям необходимо предоставить комиссии пакет документов, который включает в себя свидетельство о рождении ребенка, паспорт одного из законных представителей, медкарту ребенка, документ, который подтверждает льготу (при ее наличии). Комиссия принимает решение и выдает направление в детский сад. Также в комиссии помогут с выбором ДОУ с учетом особенностей и состояния здоровья ребенка.

Право на внеочередной прием в детские сады имеют:

• дети-сироты, усыновленные, приемные, находящиеся под опекой;
• дети, чьи родители в детском возрасте остались без попечения родителей;
• дети граждан-инвалидов (если инвалидность наступила вследствие аварии на ЧАЭС);
• дети судей, следователей, прокуроров.

На первоочередной прием в ДОУ имеют право:

• дети из многодетных семей;
• дети сотрудников милиции, военных;
• дети, один из родителей которых имеет инвалидность.

Дети одиноких родителей и педагогических работников имеют преимущественное право приема. Кроме того, на преимущественное право могут рассчитывать дети, чьи родные братья и сестры уже посещают группы данного ДОУ.

Нормативно-правовая база в деятельности ДОУ

Определение

Нормативно-правовая база дошкольного образования — это документы международного, федерального, регионального уровня, а также уровня ДОУ.

Документы международного уровня:

1. Декларация прав ребенка (1959 г.).
2. Конвенция ООН о правах ребенка (1989 г.).

Документы федерального уровня:

1. Конституция РФ.
2. Семейный кодекс Российской Федерации от 01.01.01 г. N 223-ФЗ (с изменениями и дополнениями).
3. Федеральный закон РФ «Об образовании в Российской Федерации».
4. Приказ Министерства образования науки России «Об утверждении федерального государственного образовательного стандарта дошкольного образования».

Региональные документы варьируются в зависимости от субъекта (область, край, республика и так далее).

Примеры документов уровня ДОУ:

Что такое дисперсия в статистике?

В статистике дисперсия — это измерение, указывающее на разброс или дисперсию точек данных в наборе данных. Он измеряет, насколько далеко каждое число в наборе данных от среднего (среднего) и, следовательно, от любого другого числа в наборе. Как правило, ВогоньsОн часто обозначается символом σ² и Он используется для определения постоянства доходности инвестиций в течение периода, волатильности рыночных ценных бумаг и наилучшего распределения активов в портфеле.

Различают два типа дисперсии: популяционная и выборочная.s. 

• Дисперсия населения: это дисперсия всего населения. Он рассчитывается путем взятия среднего квадрата отклонений от среднего значения для всех точек данных в совокупности.
• Выборочная дисперсия: это дисперсия подмножества или выборки населения. Он рассчитывается путем получения средних квадратов отклонений от среднего для точек данных в выборке. It используется для оценки дисперсии населенияs поскольку часто невозможно собрать данные по всему населению.

Какое другое слово для дисперсии в статистике?

Другое слово для обозначения дисперсии в статистике — «дисперсия». Отклонения Он мера дисперсии, которая обычно измеряет, насколько далеко набор чисел разбросан от их среднего значения. 

Вычисление дисперсии

Дисперсия – это показатель вариации, который представляет собой средний квадрат отклонений от математического ожидания. Таким образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.

Способ 1: расчет по генеральной совокупности

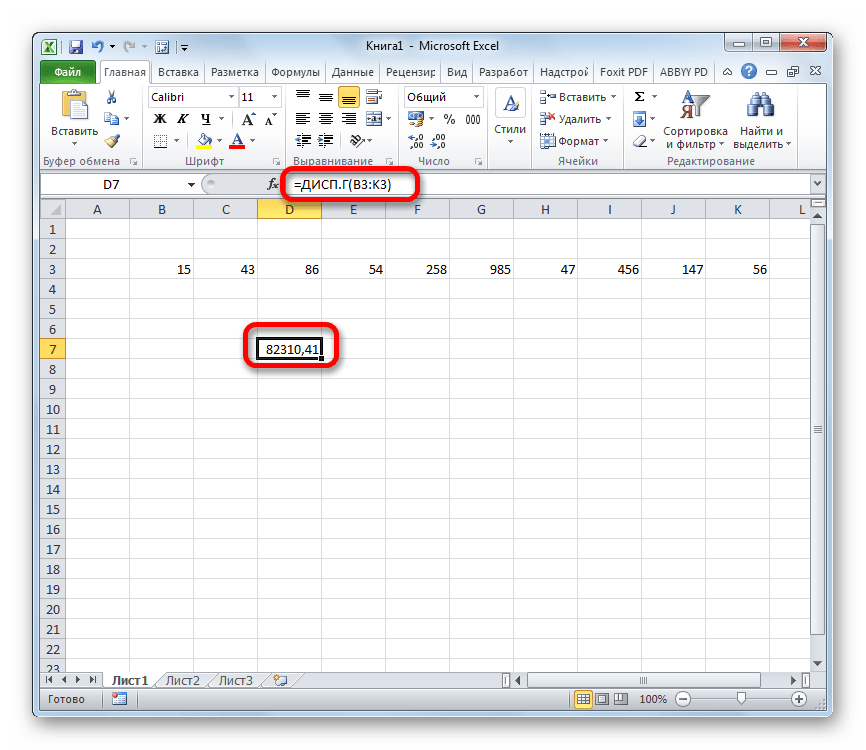
Для расчета данного показателя в Excel по генеральной совокупности применяется функция ДИСП.Г. Синтаксис этого выражения имеет следующий вид:

Всего может быть применено от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.

Посмотрим, как вычислить это значение для диапазона с числовыми данными.

1. Производим выделение ячейки на листе, в которую будут выводиться итоги вычисления дисперсии. Щелкаем по кнопке «Вставить функцию», размещенную слева от строки формул.
2. Запускается Мастер функций. В категории «Статистические» или «Полный алфавитный перечень» выполняем поиск аргумента с наименованием «ДИСП.Г». После того, как нашли, выделяем его и щелкаем по кнопке «OK».
3. Выполняется запуск окна аргументов функции ДИСП.Г. Устанавливаем курсор в поле «Число1». Выделяем на листе диапазон ячеек, в котором содержится числовой ряд. Если таких диапазонов несколько, то можно также использовать для занесения их координат в окно аргументов поля «Число2», «Число3» и т.д. После того, как все данные внесены, жмем на кнопку «OK».
4. Как видим, после этих действий производится расчет. Итог вычисления величины дисперсии по генеральной совокупности выводится в предварительно указанную ячейку. Это именно та ячейка, в которой непосредственно находится формула ДИСП.Г.

Урок: Мастер функций в Эксель

Способ 2: расчет по выборке

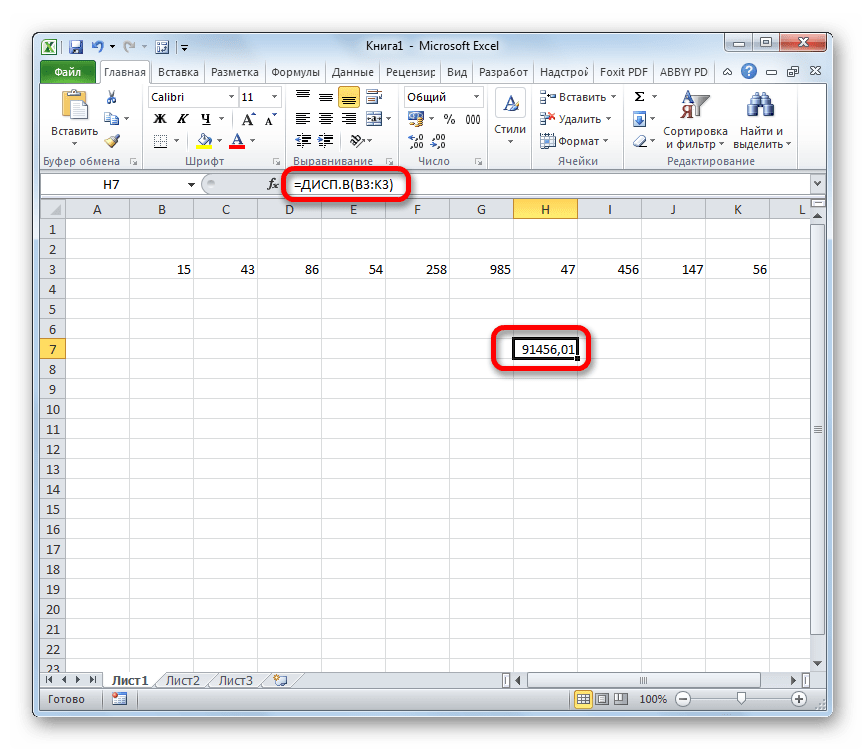
В отличие от вычисления значения по генеральной совокупности, в расчете по выборке в знаменателе указывается не общее количество чисел, а на одно меньше. Это делается в целях коррекции погрешности. Эксель учитывает данный нюанс в специальной функции, которая предназначена для данного вида вычисления – ДИСП.В. Её синтаксис представлен следующей формулой:

Количество аргументов, как и в предыдущей функции, тоже может колебаться от 1 до 255.

1. Выделяем ячейку и таким же способом, как и в предыдущий раз, запускаем Мастер функций.
2. В категории «Полный алфавитный перечень» или «Статистические» ищем наименование «ДИСП.В». После того, как формула найдена, выделяем её и делаем клик по кнопке «OK».
3. Производится запуск окна аргументов функции. Далее поступаем полностью аналогичным образом, как и при использовании предыдущего оператора: устанавливаем курсор в поле аргумента «Число1» и выделяем область, содержащую числовой ряд, на листе. Затем щелкаем по кнопке «OK».
4. Результат вычисления будет выведен в отдельную ячейку.

Урок: Другие статистические функции в Эксель

Как видим, программа Эксель способна в значительной мере облегчить расчет дисперсии. Эта статистическая величина может быть рассчитана приложением, как по генеральной совокупности, так и по выборке. При этом все действия пользователя фактически сводятся только к указанию диапазона обрабатываемых чисел, а основную работу Excel делает сам. Безусловно, это сэкономит значительное количество времени пользователей.

Свойства математического ожидания и дисперсии

Свойства математического ожидания:

1. Линейность: математическое ожидание суммы двух или более случайных величин равно сумме их математических ожиданий.
2. Постоянство относительно сдвига: математическое ожидание случайной величины, увеличенной на постоянное число, равно математическому ожиданию исходной случайной величины, увеличенной на это число.
3. Постоянство относительно масштабирования: математическое ожидание случайной величины, умноженной на постоянное число, равно произведению этого числа на математическое ожидание исходной случайной величины.

Свойства дисперсии:

1. Линейность: дисперсия суммы двух или более случайных величин равна сумме их дисперсий.
2. Постоянство относительно сдвига: дисперсия случайной величины, увеличенной на постоянное число, остается неизменной.
3. Постоянство относительно масштабирования: дисперсия случайной величины, умноженной на постоянное число, равна произведению квадрата этого числа на дисперсию исходной случайной величины.
4. Неравенство Чебышева: доля значений случайной величины, отклоняющихся от ее математического ожидания на величину, большую чем кратное ее стандартного отклонения, ограничена сверху постоянной величиной меньше или равной единице.

Знание свойств математического ожидания и дисперсии позволяет проводить более точные статистические анализы и делать выводы на основе имеющихся данных. Эти свойства являются фундаментальными и применяются во множестве областей, таких как экономика, физика, социология и другие.

Вопрос-ответ:

Как вычислить математическое ожидание и дисперсию?

Для вычисления математического ожидания нужно умножить каждое значение случайной величины на его вероятность и сложить полученные произведения. Для вычисления дисперсии нужно вычислить среднеквадратичное отклонение случайной величины от ее математического ожидания и возвести его в квадрат.

Какие формулы нужно использовать для вычисления математического ожидания и дисперсии?

Формула для вычисления математического ожидания: E(X) = Σ(x * P(x)), где X — случайная величина, x — значения случайной величины, P(x) — вероятность каждого значения. Формула для вычисления дисперсии: Var(X) = Σ((x — E(X))^2 * P(x)), где X — случайная величина, x — значения случайной величины, E(X) — математическое ожидание, P(x) — вероятность каждого значения.

Какие значения может принимать математическое ожидание и дисперсия?

Математическое ожидание может принимать любое вещественное число. Дисперсия всегда неотрицательна, она может быть равна нулю, если все значения случайной величины равны одному числу.

Какую роль играет математическое ожидание и дисперсия в статистике?

Математическое ожидание и дисперсия являются основными характеристиками случайной величины. Математическое ожидание показывает среднее значение случайной величины, а дисперсия показывает степень разброса значений случайной величины относительно ее математического ожидания. Они используются для анализа и сравнения различных случайных величин, а также для принятия решений в статистике и экономике.

Есть ли другие способы вычисления математического ожидания и дисперсии?

Да, существуют различные методы для вычисления математического ожидания и дисперсии, в зависимости от типа случайной величины и доступных данных. Например, для дискретной случайной величины можно использовать таблицу вероятностей или программное обеспечение для вычисления математического ожидания и дисперсии. Для непрерывной случайной величины можно использовать интегралы или специальные формулы. В некоторых случаях также можно применять методы численного анализа, такие как метод Монте-Карло.

Что такое математическое ожидание?

Математическое ожидание — это среднее значение случайной величины, которое ожидается получить в результате многократного проведения эксперимента.

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

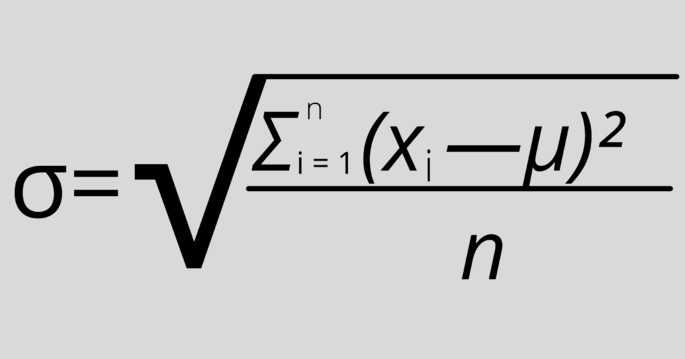Где:
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

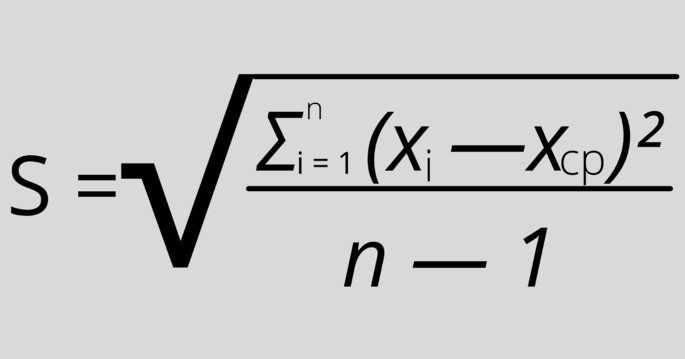Где:
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

• только её часть – используется формула S (с «n–1»),
• полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

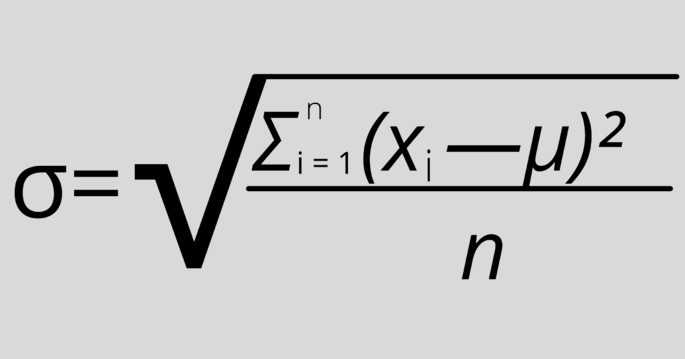
Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 — μ)² = (-5)² = 25

(x2 — μ)² = 6² = 36

(x3 — μ)² = (-5)² = 25

(x4 — μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

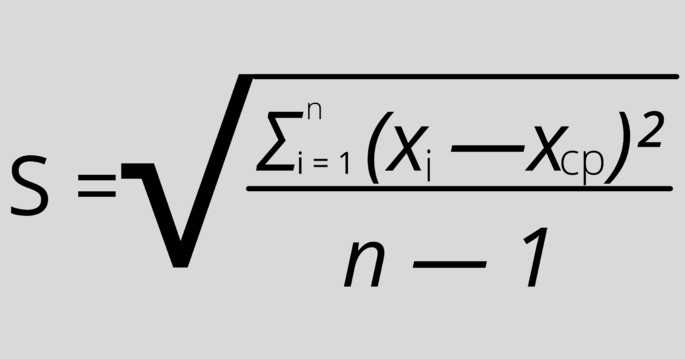
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Другие виды групп

В дошкольных учреждениях могут работать и другие виды групп.

Летняя — временная группа, организуемая летом для детей разного возраста. Занятия в них обычно не проводят, а организуют досуг: с детьми играют, читают, водят их на экскурсии, в театры или музеи.

Группа для детей раннего возраста (от 2 месяцев до 3 лет) для развития, присмотра, ухода и оздоровления.

Группа по присмотру и уходу, без реализации образовательной программы для детей от 2 месяцев до 7 лет.

Семейные дошкольные группы общеразвивающей направленности.

Соотношение групп разных видов ничем не регламентируется — группы в ДОО открывают исходя из потребности и наполненности.

В каждую из групп могут входить дети как одного возраста, так и разных возрастов. Это зависит от общей наполняемости детского сада. Работе воспитателя в разновозрастных группах мы посвятили отдельную статью.

Где получить нужные знания для работы в группах разной направленности

Работа в любой из перечисленных выше групп требует наличия определенных знаний и навыков. Мы в АНО «НИИДПО» разработали самые востребованные программы профессиональной переподготовки и повышения квалификации для воспитателей, где в концентрированной форме даются необходимые знания. Ссылки на полезные курсы вы найдете в каждом разделе выше.

Чтобы поступить на курс и начать учиться, вам не нужно приезжать в институт. Весь процесс построен дистанционно*. Просто выбирайте интересующую программу и записывайтесь — набор в группы не ограничен сроками. Учитесь в удобное время и в любом месте: Слушайте лекции и вебинары, изучайте дополнительные материалы, выполняйте практические задания и проходите тесты.

Успешно освоив программу и сдав итоговое тестирование, вы получите удостоверение, которое сможете предъявить по месту работы для подтверждения своей квалификации.

Присоединяйтесь к числу Слушателей АНО «НИИДПО», получайте новые знания, чтобы ваша работа приносила больше пользы и удовлетворения!

* Форма обучения — заочная. Образовательные программы реализуются с применением электронного обучения, дистанционных образовательных технологий.

Спасибо! Ваша заявка отправлена

Наш специалист свяжется с Вами

Автор статьи:
ДолженкоЮлия Ростиславовна

Преподаватель педагогических дисциплин, педагог-организатор, педагог дополнительного образования, специалист школьной службы медиации, обладатель Почетных грамот и благодарственных писем городского и областного уровня.

Другие статьи автора

• Как воспитателю пройти аттестацию на соответствие занимаемой должности?
• Работа воспитателя в развивающем центре. Особенности, плюсы и минусы
• Индивидуальный образовательный маршрут в работе с одаренными детьми

Все статьи этого автора

Поделитесь этой новостью в социальной сети!

2.3 Независимые величины

Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:

Px∈X,y∈Y=Px∈X⋅Py∈Y.

Обозначим отклонения величин от их средних как Δ⁢x=x-x¯ и
Δ⁢y=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δ⁢x¯=x¯-x¯=,
Δ⁢y¯=. Из независимости величин x и y следует,
что среднее значение от произведения Δ⁢x⋅Δ⁢y¯
равно произведению средних Δ⁢x¯⋅Δ⁢y¯
и, следовательно, равно нулю:

Δ⁢x⋅Δ⁢y¯=Δ⁢x¯⋅Δ⁢y¯=.

(2.6)

Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения ()
следует, что среднее суммы равно сумме средних:

z¯=x¯+y¯.

Найдём дисперсию σz2. В силу независимости имеем

Δ⁢z2¯=Δ⁢x2¯+Δ⁢y2¯+2⁢Δ⁢x⋅Δ⁢y¯≈Δ⁢x2¯+Δ⁢y2¯,

то есть:

σx+y2=σx2+σy2.

(2.7)

Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.

Подчеркнём, что для справедливости соотношения ()
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.

Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2⁢x. Здесь y и x, очевидно, зависят друг от друга. Используя
(), находим σ2⁢x=2⁢σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2⁢x=2⁢σx.

Отдельно стоит обсудить математическую структуру формулы ().
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.

Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.

коэффициент вариации

– это отношение стандартного отклонения к средней, выраженное в процентах:

И вот теперь совершенно без разницы, в д.е. мы считали:

или в тысячах д.е.:

Примечание: на практике часто считают именно через , но для оценки коэффициента вариации всей генеральной совокупности, конечно же, корректнее использовать исправленное стандартное отклонение .

В статистике существует следующий эмпирический ориентир:

– если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство вариант находится недалеко от средней, и найденное значение  хорошо характеризует центральную тенденцию совокупности.

– если показатель вариации составляет существенно больше 30%, то совокупность неоднородна, то есть, значительное количество вариант находятся далеко от , и выборочная средняя плохо характеризует типичную варианту. В таких случаях целесообразно рассмотреть , а иногда и перцентили, которые делят вариационный ряд на части, и для каждого участка рассчитать свои показатели. Но это уже немного дебри статистики.

Другое преимущество относительных показателей – это возможность сравнивать разнородные статистические совокупности. Например, множество слонов и множество хомячков. Совершенно понятно, что дисперсия веса слонов по отношению к дисперсии веса хомяков будет просто конской, и их сопоставление не имеет смысла. Но вот анализ коэффициентов вариации веса вполне осмыслен, и может статься, что у слонов он составляет 10%, а у хомячков 40% (пример, конечно, условный). Это говорит о сбалансированном питании и размеренной жизни слонов. А вот хомяки там, то носятся с голодухи по полям, то отъедаются и спят в норах, и поэтому среди них есть много худощавых и много упитанных особей

Кроме коэффициента вариации, существуют и другие относительные показатели, но в реальных студенческих работах они почти не встречаются, и поэтому я не буду их рассматривать в рамках данного курса.

И сейчас, конечно же, задачки для самостоятельного решения:

Пример 17, на отработку терминов и формул:

а) Стандартное отклонение выборочной совокупности равно 5, а средний квадрат её вариант – 250. Найти выборочную среднюю.

б) Определите среднее квадратическое отклонение, если известно, что средняя равна 260, а коэффициент вариации составляет 30%.

и Пример 18, творческий:

Производство стальных труб на предприятии (тонн) в 1-м полугодии составило:

Определить:
– среднемесячный объем производства;
– среднее квадратическое отклонение;
– коэффициент вариации.

Сделать краткие содержательные выводы. – Да, это тоже типичный пункт статистической задачи!

Обратите внимание, что здесь не понятно, выборочной ли считать эту совокупность или генеральной. И в таких случаях лучше не заниматься домыслами, просто используем обозначения без подстрочных индексов

Вообще, задачи на экономическую и промышленную тематику – самые популярные в статистике, и в моей коллекции их сотни. Но все они до ужаса однотипны, и поэтому я предлагаю их в терапевтической дозировке

Задание 8

Выполнить расчёты в Экселе – числа уже там, ну а инструкцию я на этот раз не привёл, поскольку люди вы уже опытные.

Краткое решение и ответ в конце урока, который подошёл к концу.

Следующее занятие не за горами, а уже за кочкой:

Решения и ответы:

Пример 17. Решение:

а) Используем формулу . По условию, , . Таким образом:

б) Используем формулу . По условию, , . Таким образом:

Ответ: а) , б)

Пример 18. Решение: вычислим сумму вариант и сумму их квадратов:Найдём среднюю: тонны – среднемесячный объем производства за полугодие.Дисперсию вычислим по формуле:Среднее квадратическое отклонение: тонн.Коэффициент вариации:

Ответ:  тонны,  тонн,

Краткие выводы: за первое полугодие среднемесячный объём производства труб составил  тонны. Низкие показатели вариации говорят о стабильной ситуации на производстве.

(Переход на главную страницу)

Государственные детские сады

Именно на них простирается электронная очередь, созданная в Украине для удобства в 2014 году. Это наиболее экономичный, распространенный и популярный вид ДУЗ. Они полностью подчиняются предписаниям государственных органов, как в образовательном, так и медицинском плане. Питание, развивающие занятия, методы оздоровления, гигиена быта и прочие нормы для всех казенных садиков одинаковы.

Они есть в каждом дворе, и если между ними имеются какие-то отличия, то только благодаря человеческому фактору – отношению персонала к своей работе.

• Плюсы таких учреждений: близость к дому и дешевизна.
• Минусы: плотно укомплектованные группы, из-за плохого финансирования постоянные денежные сборы с родителей, зачастую ощущается дефицит методического материала, весьма скромное питание, недостаточно комфортная среда и мало профессиональных педагогов.

Статья 23 Закон об Образовании в РФ 2015 (Новый!) . Типы образовательных организаций

1. Образовательные организации подразделяются на типы в соответствии с образовательными программами, реализация которых является основной целью их деятельности.

2. В Российской Федерации устанавливаются следующие типы образовательных организаций, реализующих основные образовательные программы:

1) дошкольная образовательная организация — образовательная организация, осуществляющая в качестве основной цели ее деятельности образовательную деятельность по образовательным программам дошкольного образования, присмотр и уход за детьми;

2) общеобразовательная организация — образовательная организация, осуществляющая в качестве основной цели ее деятельности образовательную деятельность по образовательным программам начального общего, основного общего и (или) среднего общего образования;

3) профессиональная образовательная организация — образовательная организация, осуществляющая в качестве основной цели ее деятельности образовательную деятельность по образовательным программам среднего профессионального образования;

4) образовательная организация высшего образования — образовательная организация, осуществляющая в качестве основной цели ее деятельности образовательную деятельность по образовательным программам высшего образования и научную деятельность.

3. В Российской Федерации устанавливаются следующие типы образовательных организаций, реализующих дополнительные образовательные программы:

1) организация дополнительного образования — образовательная организация, осуществляющая в качестве основной цели ее деятельности образовательную деятельность по дополнительным общеобразовательным программам;

2) организация дополнительного профессионального образования — образовательная организация, осуществляющая в качестве основной цели ее деятельности образовательную деятельность по дополнительным профессиональным программам.

4. Образовательные организации, указанные в частях 2 и 3 настоящей статьи, вправе осуществлять образовательную деятельность по следующим образовательным программам, реализация которых не является основной целью их деятельности:

1) дошкольные образовательные организации — дополнительные общеразвивающие программы;

2) общеобразовательные организации — образовательные программы дошкольного образования, дополнительные общеобразовательные программы, программы профессионального обучения;

3) профессиональные образовательные организации — основные общеобразовательные программы, программы профессионального обучения, дополнительные общеобразовательные программы, дополнительные профессиональные программы;

4) образовательные организации высшего образования — основные общеобразовательные программы, образовательные программы среднего профессионального образования, программы профессионального обучения, дополнительные общеобразовательные программы, дополнительные профессиональные программы;

5) организации дополнительного образования — образовательные программы дошкольного образования, программы профессионального обучения;

6) организации дополнительного профессионального образования — программы подготовки научно-педагогических кадров, программы ординатуры, дополнительные общеобразовательные программы, программы профессионального обучения.

5. Наименование образовательной организации должно содержать указание на ее организационно-правовую форму и тип образовательной организации.

6. В наименовании образовательной организации могут использоваться наименования, указывающие на особенности осуществляемой образовательной деятельности (уровень и направленность образовательных программ, интеграция различных видов образовательных программ, содержание образовательной программы, специальные условия их реализации и (или) особые образовательные потребности обучающихся) , а также дополнительно осуществляемые функции, связанные с предоставлением образования (содержание, лечение, реабилитация, коррекция, психолого-педагогическая поддержка, интернат, научно-исследовательская, технологическая деятельность и иные функции) .

Источник ipipip.ru

Типы и виды образовательных учреждений | Статьи | Справочник руководителя образовательного учреждения

Существует и другой принцип классификации образовательных учреждений — в зависимости от особенностей их правового положения.

В настоящее время согласно Федеральному закону от 08.05.2010 № 83-ФЗ «О внесении изменений в отдельные законодательные акты Российской Федерации в связи с совершенствованием правового положения государственных (муниципальных) учреждений» все государственные и муниципальные учреждения, в т. ч. дошкольного и общего образования, делятся на три типа:

• автономные;
• бюджетные;
• казенные.

Для того чтобы узнать, чем они отличаются, введите в строку поиска новый запрос «Автономные, бюджетные и казенные учреждения«. Первый документ в списке полученных в результате поиска материалов позволит узнать основные отличия казенных образовательных учреждений от автономных и бюджетных (рис. 2) .

Рис. 2

Искать информацию в электронной системе «Образование» можно не только с помощью строки поиска, но и с помощью рубрикатора. Он расположен на Главной странице и представляет собой набор корневых тематических рубрик, входящих в них подрубрик и материалов. Для того чтобы увидеть подрубрики и входящие в них материалы, необходимо нажать на значок «+» перед названием рубрики.

Раскройте первую рубрику «Управление образовательным учреждением» и сразу увидите искомое — подрубрику «Типы и виды ОУ». Она, в свою очередь, состоит из трех подрубрик:

1. «Экспертные материалы»;
2. «Шаблоны и примеры»;
3. «Нормативная база».

Если нажать на плюс перед названием подрубрики «Экспертные материалы», появится список ответов экспертов на вопросы, которые от- носятся к интересующей нас теме (рис. 3) .

Рис. 3

В подрубрике «Шаблоны и примеры» находятся локальные акты учреждений разных типов, в т. ч. уставы автономного, бюджетного и казенного образовательных учреждений, а в подрубрике «Нормативная база» — нормативные документы: Федеральный закон от 08.05.2010 № 83-ФЗ «О внесении изменений в отдельные законодательные акты Российской Федерации в связи с совершенствованием правового положения государственных (муниципальных) учреждений», Федеральный закон от 12.01.1996 № 7-ФЗ «О некоммерческих организациях» и др. Любой документ можно открыть, кликнув на его названии левой кнопкой мыши.

УЗНАЙТЕ БОЛЬШЕ об электронной системе «Образование», получив

Источник www.menobr.ru

Разновидности деятельности сотрудников ДОУ

Работа педагога детского дошкольного учреждения разнообразна и состоит из множества различных элементов. Каждый из них направлен на развитие определенных качеств ребенка, а суммарно все они позволяют получить гармонично развитую личность, превосходно подготовленную к функционированию к новой среде – в школе.

В состав профессиональных обязанностей каждого педагогического сотрудника дошкольного детского учреждения входят следующие:

• Педагогическая деятельность воспитателя детского сада. Она направлена на развитие социальных навыков воспитанников, защиту их прав и интересов, развитие грамотной, четкой и правильной и речи ребенка, формирование базовых знаний в математике. В это направление входит внедрение сюжетно-ролевых игр и инновационных методик обучения, проведение занятий по физической культуре, наблюдение за природой и природными явлениями, поведением домашних животных в живом уголке, а также соблюдение гигиенических норм и правил. Благодаря всему этому дети могут получить базовые знания в разных областях жизни, которые разовьют их как личность, сформируют характер и помогу стать полноправным членом общества.
• Проектная деятельность воспитателей детского сада. Целью этого метода воспитания является формирование творческой личности ребенка, способного самовыражаться через собственные способности и умения. Проектная деятельность имеет множество вариантов, связанных с возрастом воспитанников и стоящими перед ними задачами. Проекты в ДОУ могут быть исследовательско-творческими, ролево-игровыми, информационными, ориентированными на практическое применение результатов исследования, и творческими. Все разновидности проектной деятельности в детском саду позволяют раскрыть потенциал воспитанников и научить их получать и использовать необходимую информацию.
• Исследовательская деятельность работника детского сада. С момента своего появления на свет ребенок находится в состоянии непрерывного познания мира вокруг себя. Задача специалиста ДОУ состоит в том, чтобы грамотно направить эту активность в необходимое русло, обеспечить ребенку безопасность и заинтересовать его определенными темами. Чем больше малыш видит и познает, тем более гармоничной и прекрасно развитой личностью он становится.
• Методическая деятельность воспитателя детского сада играет важную роль в качестве и эффективности педагогического процесса. Методическая работа – это творческий комплексный процесс, включающий в себя постоянное совершенствование приемов и методов обучения и воспитания подрастающего поколения.

Содержание деятельности воспитателя детского сада включает и обязанности по своевременному и грамотному составлению необходимой документации, участие в реализации основных образовательных и воспитательных программ, повышение компетентности и внедрение инновационных методик.