Занятие 4. инженерные методы определения напряжений. внутренние усилия

Слайд 3Закон Гука при срезеЗакон Гука при сдвиге. Касательные напряжения, возникающие

в поперечном сечении бруса при чистом сдвиге прямо пропорциональны относительному

сдвигу:

где G- модуль сдвига, или модуль упругости второго рода; γ — относительный сдвиг.

Модулем сдвига или модулем упругости второго рода G, называется физическая постоянная материала характеризующая его способность сопротивляться упругим угловым деформациям, вызванными действием касательных напряжений. Практически для всех марок стали модуль сдвига одинаков и равен G=8,1·104 МПа.

Модуль сдвига G, модулем упругости Е и коэффициент Пуассона μ взаимосвязаны между собой по следующей зависимости:

Сдвиг (срез)

Напряжения при сдвиге

Сдвигом называют такой вид деформации, при которой в любом поперечном сечении бруса возникает только поперечная сила. Деформацию сдвига можно наблюдать, например, при резке ножницами металлических полос или прутков, при пробивании отверстия в заготовках на штампе (рис. 1) .

Рассмотрим брус площадью поперечного сечения А , перпендикулярно оси которого приложены две равные и противоположно направленные силы F ; линии действия этих сил параллельны и находятся на относительно небольшом расстоянии друг от друга. Для определения поперечной силы Q применим метод сечений (рис. 2) . Во всех точках поперечного сечения действуют распределенные силы, равнодействующую которых определим из условия равновесия оставленной части бруса:

Σ Y = 0 » F – Q = 0 ,

откуда поперечная сила Q может быть определена, как:

Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении бруса при сдвиге. Очевидно, что при сдвиге в поперечном сечении возникают только касательные напряжения τ .

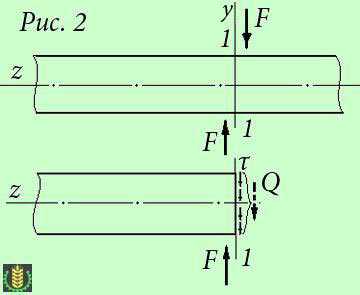
Предполагаем, что эти касательные напряжения равномерно распределены по сечению, и, следовательно, могут быть вычислены по формуле:

На основании полученной формулы можно сделать вывод, что форма сечения на величину напряжения при деформации сдвига не влияет.

Расчеты на прочность при сдвиге

Условие прочности детали конструкции заключается в том, что наибольшее напряжение, возникающее в ней (рабочее напряжение), не должно превышать допускаемое. Расчетная формула при сдвиге:

читается следующим образом: касательное напряжение при сдвиге не должно превышать допускаемое . (при обозначении предельно допустимых напряжений применяют квадратные скобки: или ) По этой расчетной формуле проводят проектный и проверочный расчеты и определяют допускаемую нагрузку.

Деформация сдвига, доведенная до разрушения материала, называется срезом (применительно к металлам) или скалыванием (применительно к неметаллам). Допускаемое напряжение на срез выбирают для пластичных материалов в зависимости от предела текучести. В машиностроении для штифтов, болтов, шпонок и других деталей, работающих на срез принимают [τ_ср] = (0,25….0,35) σ_т, где σ_т – предел текучести материала изделия.

При расчетах на срез в случае, если соединение осуществляется несколькими одинаковыми деталями (болтами, заклепками и т. д.), полагают, что все они нагружены одинаково. Расчеты соединений на срез обычно сопровождают проверкой прочности этих соединений на смятие.

Деформация Гука при сдвиге

Для установления параметров, характеризующих деформацию при сдвиге, рассмотрим элемент бруса в виде параллелепипеда abcd , на грани которого действуют только касательные напряжения τ , а противоположную грань параллелепипеда представим жестко защемленной (рис. 3) .

Деформация сдвига в указанном элементе заключается в перекашивании прямых углов параллелепипеда за счет поступательного перемещения грани bc по отношению к сечению, принятому за неподвижное. Деформация сдвига характеризуется углом γ (гамма) и называется углом сдвига , или относительным сдвигом . Величина bb₁ , на которую смещается подвижная грань относительно неподвижной, называется абсолютным сдвигом . Относительный сдвиг γ выражается в радианах.

Напряжения и деформации при сдвиге связаны между собой зависимостью, которая называется закон Гука при сдвиге. Закон Гука при сдвиге справедлив лишь в определенных пределах нагрузок и формулируется так: касательное напряжение прямо пропорционально относительному сдвигу .

Математически закон Гука для деформации сдвига можно записать в виде равенства:

Коэффициент пропорциональности G характеризует жесткость материала, т. е. способность сопротивляться упругим деформациям при сдвиге, и называется модулем сдвига или модулем упругости второго рода .

Модуль упругости выражается в паскалях; для различных материалов его величина определена экспериментально и ее можно найти в специальных справочниках. При проведении ответственных расчетов на срез величина модуля упругости для каждого соединения определяется опытным путем, непосредственно перед расчетом, либо берется из справочника с применением увеличенного запаса прочности.

Следует отметить, что между тремя упругими постоянными (модулями упругости) E , G и ν существует следующая зависимость:

Принимая для сталей ν ≈ 0,25, получаем: G_ст ≈ 0,4 Е_ст .

Материалы раздела «Сопротивление материалов»:

4.3. Статический способ определения внутренних усилий

Пусть под действием приложенной внешней нагрузки (рис.4.10)
стержень находится в равновесии (дана самоуравновешенная система сил),
т. е. для внешних сил выполняются условия

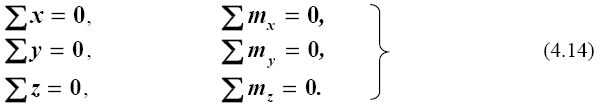
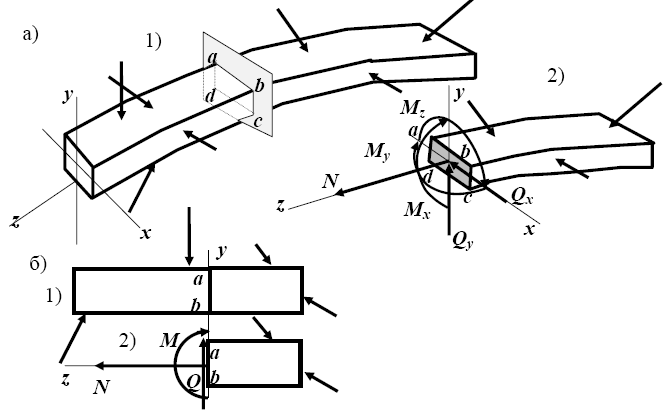
Рис. 4.10. Внутренние усилия в сечении стержня в пространстве (а)
и на плоскости (б)
1 — общий вид стержня;
2- отсеченная его часть

Любая часть стержня должна находиться в равновесии под
действием внешней нагрузки и внутренних усилий. Разделим стержень
сечением abсd на две части. Чтобы не нарушить их равновесия, усилия в
рассеченных связях заменим интегральными силовыми характе-
ристиками (рис. 4.10). Ими должны быть: продольное усилие N,
изгибающие моменты M_x ,M_y; крутящий момент M_z; поперечные силы Q_x,
Q_y(шесть параметров соответствуют шести степеням свободы плоского
сечения или шести макросвязям). Для части стержня также должны быть
справедливы уравнения равновесия (4.14), но только теперь в них войдут
неизвестные внутренние усилия

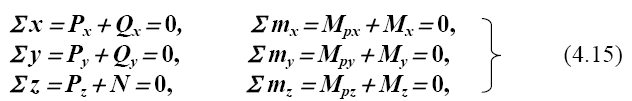
где P_x ,P_y, P_z — проекции приложенных к отсеченной части стержня
внешних сил соответственно на оси x, y, z; M_px, M_py, M_pz— моменты
внешних сил относительно осей x, y, z.

Допущение о малости перемещений дает возможность в уравнения
(4.15) ввести геометрические параметры (размеры, очертания осей или
углы наклона сил и их плечи) недеформированного состояния. Ввиду
этого число уравнений равновесия равно числу неизвестных, система
является статически определимой. При решении плоской задачи будут
иметь место только три внутренних усилия (M, Q, N) и три уравнения
равновесия.

Из системы (4.15) следует простой способ вычисления внутренних
усилий в любом сечении свободного незамкнутого стержня,
загруженного самоуравновешенной нагрузкой. Для этого необходимо
провести сечение, рассмотреть любую отсеченную часть стержня и
составить соответствующие уравнения равновесия.

Приведенные выше рассуждения показывают, что внутренние
усилия представляют собой интегральную характеристику
напряженного состояния сечения в целом, в то время как напряжения
определяют состояние отдельной точки сечения. Из этих же
рассуждений следует, что по известным внутренним усилиям с учетом
принятых геометрических гипотез легко могут быть найдены
напряжения. Внутренние усилия, таким образом, являются основным
инструментом анализа напряженного состояния конструкции. Поэтому
задачу вычисления внутренних усилий в строительной механике часто
называют основной.

Решение задачи определения внутренних усилий и напряжений
принято представлять в виде графиков — эпюр усилий и напряжений. Они
показывают значения усилий и характер их изменения по длине
каждого элемента сооружения и эпюр напряжений — по сечению. Эпюры
дают возможность при соответствующем опыте мгновенно оценить
состояние конструкции, увидеть опасные сечения (точки), наметить при
необходимости способы перераспределения внутренних усилий.

В анализе напряженно деформированного состояния элементов
конструкций задача определения внутренних усилий является наиболее
трудоемкой, и хотя все необходимые вычисления при этом полностью
основываются на составлении уравнений равновесия, для ее успешного
решения требуется иметь прочные практические навыки. В связи с этим мы сочли целесообразным разделить задачу на отдельные простейшие
этапы и подробно разобрать их в Приложении к настоящему курсу.

Практические расчеты на сдвиг

Расчет на сдвиг проводится для деталей, работающих в условиях, при которых внешние силы стремятся их разрушить путем сдвига. Примеры таких деталей: болты, заклепки, шпильки, шпонки и т.п. (рис.1.5).

Расчет деталей на сдвиг носит условный характер, так как для упрощения расчетов принимается ряд допущений:

— при расчете на сдвиг изгиб деталей не учитывается, считается, что в поперечном сечении возникает только один внутренний силовой фактор – поперечная сила Q;

— касательные напряжения в сечении сдвига распределены равномерно;

— в случае, если соединение осуществлено несколькими одинаковыми деталями, например болтами или заклепками, считается, что они нагружены одинаково.

На основании этих допущений условие прочности можно записать в виде

, (1.9)

где τ_с – касательные напряжения в сечении детали (заклепки, болта и т.п.),

Q_с – поперечная сила;

если одинаковых болтов или заклепок несколько, то

здесь Р – полная нагрузка на все соединение;

n – число заклепок или болтов;

F_с – площадь сдвига одной детали (болта или заклепки);

В машиностроении принимают

[ ] = (0,25 0,35) ,

где σ_т– предел текучести материала детали.

На рисунке 1.6. представлены заклепочные соединения двух видов: односрезные (рис.1.6.а) и двухсрезные (рис.1.6, б)

Для односрезной заклепки площадь среза

F _сз= d 2 _з /4,

где d_з– диаметр заклепки,

тогда площадь среза всего соединения будет равна

F_С = n d 2 _з /4.

Условия прочности заклепки по срезу примет вид

Для двухсрезных заклепок

F_с = 2 , τ_{с =}. (1.11)

Одновременно со сдвигом может произойти смятие в местах контакта элементов соединения – появление пластических деформаций под действием контактных сжимающих сил, которые условно называются напряжениями смятия _.

Расчет на смятие также носит условный характер. Условие прочности при этом записывается в виде:

, (1.12)

F _см = t_min d – площадь смятия одной детали;

t_min – наименьшая из толщин соединяемых листов;

d –диаметр болта или заклепки.

Для машиностроительных конструкций принимается = (2 2,5) ,

где – допускаемое напряжение при сжатии.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

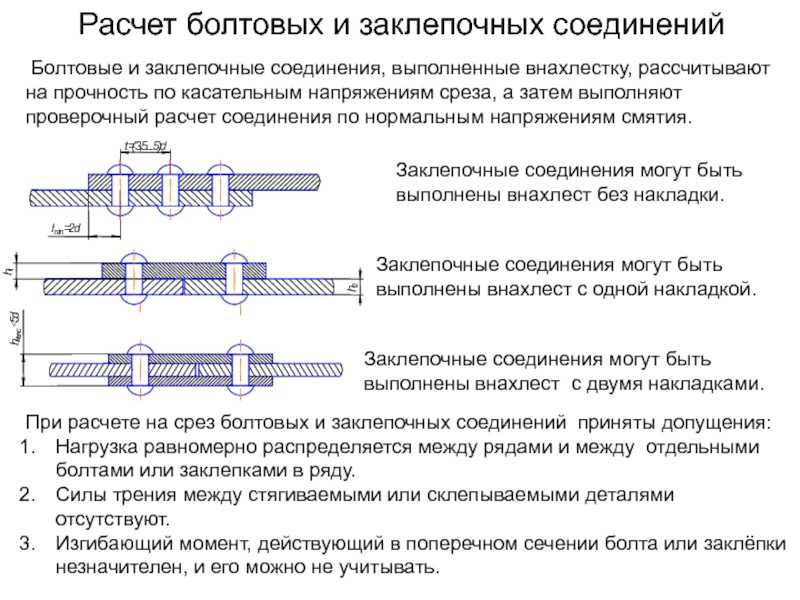
Слайд 6Расчет болтовых и заклепочных соединений Болтовые и заклепочные соединения, выполненные

внахлестку, рассчитывают на прочность по касательным напряжениям среза, а затем

выполняют проверочный расчет соединения по нормальным напряжениям смятия.

При расчете на срез болтовых и заклепочных соединений приняты допущения:Нагрузка равномерно распределяется между рядами и между отдельными болтами или заклепками в ряду.Силы трения между стягиваемыми или склепываемыми деталями отсутствуют.Изгибающий момент, действующий в поперечном сечении болта или заклёпки незначителен, и его можно не учитывать.

Заклепочные соединения могут быть выполнены внахлест с двумя накладками.

Заклепочные соединения могут быть выполнены внахлест без накладки.

Заклепочные соединения могут быть выполнены внахлест с одной накладкой.

Сдвиг (срез)

Сдвигом называется нагружение, при котором в поперечном се­чении бруса возникает только один внутренний силовой фактор — поперечная сила.

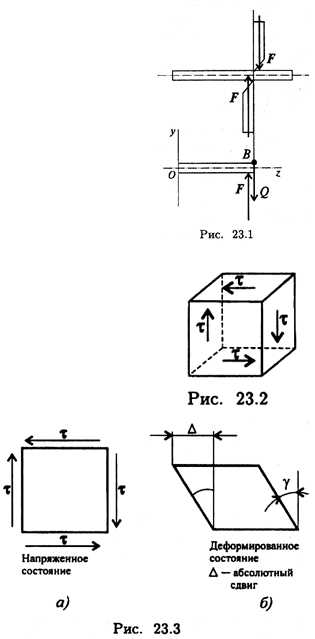
Рассмотрим брус, на который действу­ют равные по величине, противоположно направленные, перпендикулярные продоль­ной оси силы (рис. 23.1).

Применим метод сечений и определим внутренние силы упругости из условия равновесия каждой из частей бруса:

где Q — поперечная сила. Естественно считать, что она вызовет появление только касательных напряжений τ.

Рассмотрим напряженное состояние в точке В поперечного сечения.

Выделим элемент в виде бесконечно малого параллелепипеда, к граням которо­го приложены напряжения (рис. 23.2).

Исходя из условия равновесия точки В, внутри бруса при возникновении касательного напряжения τ на правой вертикальной площадке такое же напря­жение должно возникнуть и на левой площадке. Они образуют пару сил. На горизонтальных площадках возникнут такие же напряжения, образующие такую же пару обратного направления (рис. 23.3).

Такое напряженное состояние называется чистым сдвигом. Здесь действует закон парности касательных напряжений:

При сдвиге в окрест­ностях точки на взаимно перпендикулярных площад­ках возникают равные по величине касательные на­пряжения, направленные на соседних площадках ли­бо от ребра, либо к ребру (рис. 23.3а).

В результате площадки сдвигаются на угол γ, назы­ваемый углом сдвига.

При сдвиге выполняется закон Гука, который в данном случае записывается следующим образом:

Здесь τ — напряжение; G — модуль упругости сдвига; γ — угол сдвига.

При отсутствии специальных испытаний G можно рассчитать по формуле

Е — модуль упругости при растяжении.

Расчет деталей на сдвиг носит условный характер.

Для упрощения расчетов принимается ряд допущений:

— при расчете на сдвиг изгиб деталей не учитывается, хотя силы, действующие на деталь, образуют пару;

— при расчете считаем, что силы упругости распределены по сечению равномерно;

— если для передачи нагрузки используют несколько деталей, считаем, что внешняя сила распределяется между ними равномерно.

Откуда формула для расчета напряжений имеет вид:

где τ_с — касательное напряжение; Q — поперечная сила; Ас — площадь сдвига; F — внешняя сдвигающая сила; z — количество деталей.

Условие прочности при сдвиге (срезе)

[τ_с] — допускаемое напряжение сдвига, обычно его определяют по формуле

При разрушении деталь перерезается поперек. Разрушение детали под действием поперечной силы называют срезом.

Смятие

Довольно часто одновременно со сдвигом происходит смятие боковой поверхности в месте контакта в результате передачи нагрузки от одной поверхности к другой. При этом на поверхности возникают сжимающие напряжения, называемые напряжениями смятия, σ_см.

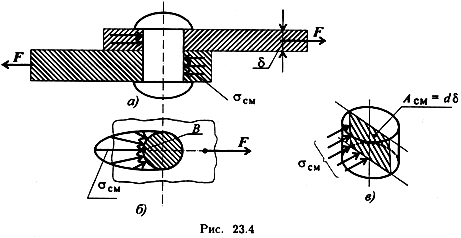Расчет также носит условный характер. Допущения подобны принятым при расчете на сдвиг (см. выше), однако при расчете боковой цилиндрической поверхности напряжения по поверхности распределены не равномерно, поэтому расчет проводят для наиболее нагруженной точки (на рис. 23.4 б). Для этого вместо боковой поверхности цилиндра в расчете используют плоскую поверхность, проходящую через диаметр. На рис. 23.4 показана примерная схема передачи давления на стержень заклепки.

Таким образом, условие прочности при смятии можно выразить соотношением

где d — диаметр окружности сечения; δ — наименьшая высота соединяемых пластин; Асм — расчетная площадь смятия; F — сила взаимодействия между деталями, допускаемое напряжение смятия:

4.4. Определение напряжений по внутренним усилиям

Если внутренние усилия известны, то на основе зависимостей (4.1) —
(4.12.) можно осуществить переход к напряжениям. Формулы определения
напряжений по внутренним усилиям для наиболее часто встречающихся
видов деформации сведем в таблице 4.4.

Таблица 4.4
Формулы для определения напряжений в поперечном сечении стержней

Вид напряженного состояния	Нормальные напряжения σ	Касательные напряжения τ
1.Центральное растяжение или сжатие		нет
2.Чистый изгиб в плоскости zoy в плоскости zox в двух плоскостях (косой чистый изгиб)		нет нет нет
3.Сдвиг (срез)	нет
4.Кручение круглого стержня	нет
5.Поперечный изгиб в плоскости zoy в плоскости zox в двух плоскостях (косой изгиб)
6.Чистый изгиб в плоскости zoy с кручением (для круглого стержня)
7.Сдвиг с кручением (для круглого стержня)	нет
8.Косой изгиб с растяжением (сжатием) — косое внецентренное растяжение (сжатие)
9.Поперечный изгиб круглого стержня в плоскости yoz с кручением
Примечание. При определении напряжений для сложных напряженных состояний, так же как при выводе прямых формул определения внутренних усилий по напряжениям, используется принцип суперпозиции (принцип независимости действия сил), поэтому все недостающие формулы легко получить самостоятельно, разложив предварительно сложное напряженное состояние на простые составляющие. Этот прием, кроме того, позволит во всех случаях довольно просто определять положение опасных точек в сечении.