Теория графов. основные понятия и виды графов

Топ вопросов за вчера в категории Информатика

Информатика 17.07.2023 18:55 326 Волков Влад

Напишите программу на языке Phyton, которая считывает одну строку. Если это пустая строка, т. е. есл

Ответов: 2

Информатика 18.06.2023 02:26 1423 Егерь Денис

Во время практической работы ученик перенёс папку с:\Общая\7 класс\7Г в папку Тексты на диске D:\. Н

Ответов: 1

Информатика 03.06.2023 20:14 450 Борисова Екатерина

На столе в красивой вазочке лежит 10002 леденцов, 278 шоколадных конфет, 3016 карамелек. Сколько все

Ответов: 2

Информатика 03.06.2023 01:51 1436 Данилин Егор

Найдите верное равенство: 1110 = 10102 178 = 11112 1916 = 1000102 208 = 1116

Ответов: 2

Информатика 03.06.2023 22:15 1893 Ли Егор

Сравните величины, указав для каждой пары величин соответствующий знак. 1008 и 6410108 и 101610101

Ответов: 2

Информатика 16.05.2023 12:31 4538 Никитичева Эмилия

Знаковой информационной моделью не является … 1) Рисунок 2) Словесное описание 3) фотография 4

Ответов: 2

Информатика 25.04.2021 00:53 1507 Буткус Алеша

По каналу связи передаются сообщения, содержащие только семь букв: А, Б, В, Г, Д, Е и Ж. Для передач

Ответов: 2

Информатика 26.09.2023 04:28 305 Микитин Петя

Найди правильное решение. Сергей закодировал двоичным кодом буквы А — 00, Б — 01, B — 10, Г — 11.

Ответов: 2

Информатика 18.06.2023 00:36 614 Тимчук Маша

Петя собирает для туристического кружка световое табло. Сколько лампочек ему нужно разместить на таб

Ответов: 1

Информатика 20.06.2023 23:44 384 Балабанов Дима

На столе в красивой вазочке лежит 110012 леденцов, 118 шоколадных конфет, 1916 карамелек. Сколько вс

Ответов: 1

Тема 2.13. Основные понятия теории графов.

Оглавление |
Назад |
Далее |
Глоссарий понятий

Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек.
Вершины, прилегающие к одному и тому же ребру, называются смежными.

Если ребра ориентированны, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом.
Если ребра не имеют ориентации, граф называется неориентированным.

Граф

Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра — линиями, соединяющими точки (рис. 2.15).

Рис. 2.15

Петля это дуга, начальная и конечная вершина которой совпадают.

Простой граф граф без кратных ребер и петель.

Степень вершины это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер.

Пустым называется граф без ребер. Полным называется граф, в котором каждые две вершины смежные.

ПУТИ, МАРШРУТЫ, ЦЕПИ и ЦИКЛЫ.

Путь в ориентированном графе — это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.

Вершины v0, vn называются связанными данным путем (или просто связанными). Вершину v0 называют началом, vn — концом пути. Если v0 = vn, то путь называют замкнутым. Число n называется длиной пути.

Маршрут в графе путь, ориентацией дуг которого можно пренебречь.
Цепь маршрут, в котором все ребра попарно различны.Цикл замкнутый маршрут, являющийся цепью.

Маршрут, в котором все вершины попарно различны, называют простой цепью. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называются простым циклом.

Граф отношения делимости

Построим граф, изображающий отношение делимости на множестве {1,2,3,4,5,6,7,8,9,10}. Принцип такой: если от одного числа до другого есть цепь, ведущая вверх, тогда второе число делится на первое (рис. 2.16).

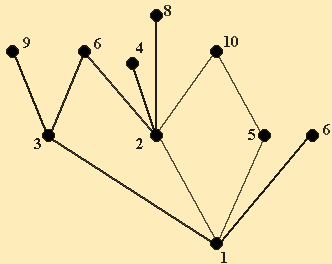
Рис. 2.16

ПОДГРАФЫ

Подграф графа это граф, являющийся подмоделью исходного графа, т.е. подграф содержит некоторые вершины исходного графа и некоторые ребра (только те, оба конца которых входят в подграф).

Подграф, порожденный множеством вершин U это подграф, множество вершин которого — U, содержащий те и только те ребра, оба конца которых входят в U.

Подграф называется остовным подграфом, если множество его вершин совпадает с множеством вершин самого графа.

Связность графа

Граф называется связным, если любая пара его вершин связана.
Связными компонентами графа называются подграфы данного графа, вершины которых связаны.

Деревья

Дерево — это связный граф без циклов.
Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярны генеалогические деревья.

Генеалогическое дерево

На рисунке 2.17 показано библейское генеалогическое дерево.

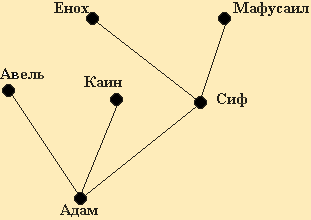
Рис. 2.17

Граф без цикла называется лесом. Вершины степени 1 в дереве называются листьями. Деревья — очень удобный инструмент представления информации самого разного вида. Деревья отличаются от простых графов тем, что при обходе дерева невозможны циклы. Это делает графы очень удобной формой организации данных для различных алгоритмов. Таким образом, понятия дерева активно используется в информатике и программировании.

Очевидно, что графический способ представления графов непригоден для ПК. Поэтому существуют другие способы представления графов.

В теории графов применяются

1. Матрица инцинденций. Это матрица А с n строками, соответствующими вершинам, и m столбцами, соответствующнго рёбрам. Для ориентированного графа столбец, соответствующий дуге (х,y) содержит — 1 в строке, соответствующей вершине х и 1, в строке, соответствующей вершине у. Во всех остальных . Петлю, т.е. дугу (х,х) можно представлять иным значением в строке х, например, 2. Если граф неориентированный, то столбец, соответствуюший ребру (х,у) содержит 1, соответствующие х и у и нули во всех остальных строках.

2. Матрица смежности. Это матрица n×n где n — число вершин, где b_ij = 1, если существует ребро, идещее из вершины х в вершину у и b_ij = 0 в противном случае.

Составим матрицы инциндентности и смежности для следующего непрерывного графа (рис. 2.18)

Рис. 2.18

Матрица инцидентности

Матрица смежности

Оглавление |
Назад |
Далее |
Глоссарий понятий

Способы задания множества

1. Перечисление: 𝐴 = {𝑎, 𝑏, 𝑐} – a,b,c являются элементами множества, и только они

   • При перечислении элементов множества порядок их перечисления не важен: {𝑎,𝑏, 𝑐} = {𝑏, 𝑐, 𝑎} = {𝑐,𝑎, 𝑏}
   • Перечисление невозможно, если:
     • Рассматриваемое множество состоит из элементов, которые нельзя указать по какой-то причине
     • Множество содержит бесконечное число элементов
     • Множество содержит слишком большое число элементов

2. Указание свойства: 𝐵 = {𝑥: 𝑥 − чётное число} – B является множеством чётных чисел.
   Способ сопоставим с предикатом P(x), принимающим значения «ИСТИНА-ЛОЖЬ»

3. Комбинированный:

   • С неполным перечислением: 𝐸 = {𝑒1, 𝑒2, … , 𝑒𝑛}
   • Буквенные обозначения:
     • ℕ − множество натуральных чисел
     • ℤ − множество целых чисел
     • ℚ − множество рациональных чисел
     • ℝ − множество действительных чисел
     • ℂ − множество комплексных чисел

Классические задачи комбинаторики

1. Размещение n предметов по k ящикам: Каждый ящик может вместить k предметов. Все предметы должны быть размещены, порядок не важен. При этом могут остаться незаполненные ящики. Каждый предмет размещается в один из k ящиков независимо от других:
   𝑘 ∗ 𝑘 ∗ 𝑘 ∗ … ∗ 𝑘 = 𝑘𝑛
2. Раскраска р предметов в r цветов: Каждый предмет может быть окрашен ровно в один цвет, краски каждого цвета хватит для окраски всех предметов. Каждый предмет красится независимо от других только в один цвет, значит, число способов перекраски равно
   𝑟𝑝
3. Количество слов длины t в заданном алфавите длины m: На каждое из t мест символ можно выбрать т способами, таким образом количество слов равно
   𝑚 ∗ 𝑚 ∗ … ∗ 𝑚 = 𝑚𝑡
   Пример: существует 32 = 9 слов длины 2 в алфавите {1,2,3}:
   • 11
   • 12
   • 13
   • 21
   • 22
   • 23
   • 31
   • 32
   • 33

Эвристические алгоритмы решения задачи коммивояжера

1. «Жадная» эвристика.
   Начинаем из вершины с наименьшим номером,
   выбираем ребро с минимальным весом,
   включаем его в путь.

   Повторяем, пока все вершины не окажутся в графе.
   Просмотренные рёбра и есть решение задачи.

2. «Ближайшая вставка»
   Начинаем из вершины с наименьшим номером,
   выбираем ребро с минимальным весом, которое в данный момент подключено к дереву,
   включаем его в путь.

   (Примерно как в )

3. Использование остовного дерева с минимальным весом.

   Построенный цикл будет не более, чем в два раза «тяжелее» оптимального.

   • 1 шаг: строим остовное дерево с минимальным весом.
   • 2 шаг: удваиваем ребра построенного дерева.
   • 3 шаг: в полученном графе строим эйлеров цикл.
   • 4 шаг: из полученного цикла удаляем повторяющиеся вершины.
   • В результате получится гамильтонов цикл.

Связный граф — граф, в котором есть хотя бы одна пара соединённых вершин.

Сильносвязный граф — граф, в котором для любой пары вершин найдётся прямая связь (ребро). (Аналог полного графа)

Слабосвязный граф — граф, в котором для любой пары вершин найдётся хотя бы 1 маршрут соединяющий их.

Односторонне достижимый граф — граф, в котором для хотя бы 1 пары вершин найдётся путь A-B, но не B-A

Несвязный граф — граф, в котором найдётся хотя бы 1 пара вершин, для которой нельзя построить маршрут, соединяющий их.

Компонента связности — Максимальный связный подграф неориентированного графа

Существуют два вида связности:

• Число вершинной связности – это наименьшее число вершин, удаление которых (вместе с инцидентными ребрами) приводит к несвязному графу.
• Число реберной связности– это наименьшее число ребер, удаление которых приводит к несвязному графу.

1 Основные понятия

В дальнейшем, если это явно не оговаривается, мы будем рассматривать только
.

Способы задания графа

1. Явное задание графа как алгебраической системы.
2. Геометрический
3. Матрица смежности
4. Матрица инцидентности

Рассмотрим различные способы задания для одного и того же графа.

1. <{a,b,c,d},{u,v,w,x};
   {(u,a),(u,b),(v,b),(v,c),(w,c),(w,a),(x,c),
   (x,d)}>.
   Так как мы рассматриваем только простые графы, граф нам проще определять как
   модель, носителем которой является множество вершин, а отношение – бинарное
   отношение смежности вершин. Тогда данный граф запишется как
   <{a,b,c,d}; {(a,b),
   (b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)}>.
   В таком представлении ребру соответствуют две пары вершин (v1,v2) и
   (v2,v1), инцидентных данному ребру.
   Чтобы задать такое представление, достаточно для каждого ребра указать
   двухэлементное множество вершин – его мы и будем отождествлять с ребром.
   Для данного графа рёбра задаются множеством
   {{a,b},{b,c},{a,c},{c,d}} и граф мы будем записывать как
   пару (V,E), где V – множество вершин, а E – множество рёбер.

   В дальнейшем мы будем опираться именно на второе определение графа.

2. Геометрический

3. Матрица смежности

	a	b	c	d
a	1	1
b	1	1
c	1	1	1
d	1

4. Матрица инцидентности

	u	v	w	x
a	1
b	1	1	1
c	1	1
d	1	1

Понятие изоморфизма для графов имеет наглядное толкование.
Представим рёбра графов эластичными нитями, связывающими узлы – вершины.
Тогда, изоморфизм можно представить как перемещение узлов и растяжение нитей.

Пример 1 (изоморфизм).
Покажем, что следующие два графа изоморфны.

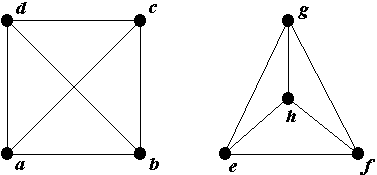
Действительно, отображение a e, b f,
c g, d h,
являющееся изоморфизмом легко представить как модификацию первого графа,
передвигающую вершину d в центр рисунка.

1.1 Постройте изоморфизм графов

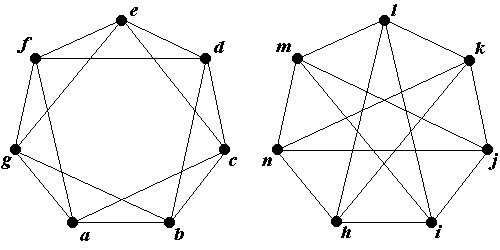
Определение 1 (Степень вершины).

Степенью вершины назовём удвоенное количество петель, инцидентных
этой вершине плюс количество остальных инцидентных ей рёбер.

1.2 Докажите, что изоморфизм сохраняет степени вершин графа. Иначе говоря,
степень образа вершины при изоморфизме совпадает со степенью самой вершины.

1.3 Проверьте, изоморфны ли графы.

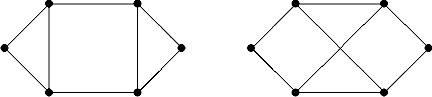
1.4 Докажите, что сумма всех степеней вершин графа равна удвоенному количеству
рёбер.

1.5 Докажите, что в любом графе количество вершин нечётной степени –
чётное число.

Подграфы

Определение 2 (Подграф).
Подграфом графа называется граф,
являющийся подмоделью исходного графа.
Иначе говоря, подграф содержит некоторые вершины исходного графа и некоторые
рёбра (только те, оба конца которых входят в подграф).

Определение 3 (Подграф, порождённый множеством вершин).

Подграфом, порождённым множеством вершин U
называется подграф, множество вершин которого – U, содержащий те и
только те рёбра, оба конца которых входят в U.

Определение 4 (Остовной подграф).
Подграф называется остовным подграфом,
если множество его вершин совпадает с множеством вершин самого графа.

Два последних определения дают два вида максимальности подграфов:
максимальность множества вершин и максимальность множества рёбер.
Это подтверждают следующие три задачи:

1.6 Докажите, что подграф H графа G является порождённым множеством
своих вершин тогда и только тогда, когда не существует ни одного
другого подграфа графа G, для которого H являлся бы остовным подграфом.

см. Решение

1.7 Докажите, что подграф H графа G является остовным
тогда и только тогда, когда не существует ни одного
другого подграфа графа G, для которого H являлся бы подграфом,
порождённым множеством своих вершин.

1.8 Докажите, что если подграф является остовным подграфом и подграфом,
порождённым множеством своих вершин одновременно,
то этот подграф – сам граф.

Определение 5 (Пустой, полный графы).
Пустым называется граф без рёбер.
Полным называется граф, в котором каждые две вершины смежны.

1.9 Докажите, что граф является пустым тогда и только тогда, когда все его
подграфы – тоже пустые.

1.10 Докажите, что граф является полным тогда и только тогда, когда все его
подграфы, порождённые некоторым множеством вершин – тоже полные.

1.11 Докажите, что полные (пустые) графы изоморфны тогда и только тогда, когда они
имеют одинаковое количество вершин.

1.12 Докажите, что пустой граф с n вершинами содержит ровно n попарно
неизоморфных подграфов.

1.13 Докажите, что граф с n вершинами является пустым тогда и только тогда,
когда он содержит ровно n попарно неизоморфных подграфов.

1.14 Докажите, что полный граф с n вершинами содержит ровно n попарно
неизоморфных подграфов, порождённых некоторыми множествами вершин.

1.15 Докажите, что граф с n вершинами является полным или пустым
тогда и только тогда,
когда он содержит ровно n попарно неизоморфных подграфов, порождённых
некоторыми множествами вершин.

История возникновения теории графов

Леонард Эйлер и задача о Кёнигсберских мостах

Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и
предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории
графов.

Издавна среди жителей Кёнигсберга (теперь Калининграда) была распространена такая загадка: как пройти по всем
мостам, не проходя ни по
одному из них дважды? Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во
время
прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно.

В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук
Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В
этом
письме
Эйлер пишет о том, что он смог найти правило, пользуясь которым легко определить, можно ли пройти по всем
мостам,
не проходя дважды ни по одному из них (в случае семи мостов Кёнигсберга это невозможно).

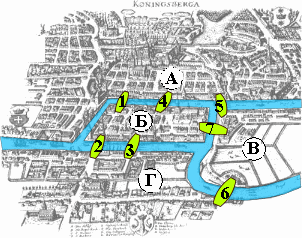
Для того, чтобы решить эту задачу, Эйлер сделал специальные обозначения. Каждую часть суши (остров или берег
реки) он обозначил кружком на бумаге, а затем соединил линиями те кружки, между которыми существуют мосты. Такие
обозначения подчеркивают, что в этой задаче фактическое расположение, форма, длина и другие свойства объектов не
представляют интереса, важны только связи между ними. Такая картинка на бумаге или на экране компьютера
называется графом. Кружки — это его вершины, а линии — рёбра. Размышляя
над этой и другими картинками из кружков и линий, Эйлер пришел к следующим выводам о графах:

• Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно всегда быть чётно. То
  есть, просто не может
  существовать графа, который имел бы нечётное число нечётных вершин.
• Если все вершины графа чётные, то его можно начертить не отрывая карандаша от бумаги, при этом начинать
  можно
  с любой вершины графа и завершить его в ней же.
• Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.

Граф кёнигсбергских мостов имел четыре нечётные вершины (т.е. все), следовательно, невозможно пройти по всем
мостам, не проходя ни по одному из них дважды.

Проблема четырёх красок

Проблема четырёх красок — математическая задача, предложенная Гутри в 1852 году.

Выяснить, можно ли всякую расположенную на сфере карту раскрасить четырьмя красками так, чтобы любые две области,
имеющие общий участок границы, были раскрашены в разные цвета.

Иначе говоря, показать что хроматическое число плоского графа не превосходит 4.

О доказательстве

К. Аппель и В. Хакен доказали в 1976 г., что так можно раскрасить любую карту. Это была первая крупная
математическая теорема, для доказательства которой был применён компьютер. Несмотря на последующие упрощения,
доказательство практически невозможно проверить, не используя компьютер. Поэтому некоторые математики отнеслись
к
этому доказательству с недоверием, что объяснялось не только использованием компьютера, но и громоздкостью
описания алгоритма первых доказательств (741 страница), впоследствии были предложены более компактные алгоритмы
и
скорректирован ряд ошибок. Проблема четырех красок является одним из известнейших прецедентов неклассического
доказательства в современной математике.

Последние заданные вопросы в категории Информатика

Информатика 16.10.2023 04:33 17 Беззубик Ксения

Информация о живой и не живой природе информатика

Ответов: 2

Информатика 16.10.2023 04:09 30 Книжников Костя

Сколько бит получится, если из 3072 килобайт вычесть 2 мегабайт и прибавить 48 байт?

Ответов: 3

Информатика 15.10.2023 23:32 16 Чопик Аня

вычислите и результат запишите в 16-той системе счисление . 10000в двоичной системе счисления +1000в

Ответов: 2

Информатика 15.10.2023 21:18 14 Арутюнян Ангелина

Для доступа к какому информационному ресурсу интернета в универсальном указателе ресурсов(URL)исполь

Ответов: 2

Информатика 15.10.2023 18:44 2 Сидоркина Венера

Дано натуральное число определить его максимальную цифру

Ответов: 2

Информатика 15.10.2023 18:14 30 Токаренко Кристина

Информатика НАРОД! СРОЧНО! СРОЧНО! ПОМОГИТЕ!Задание:1280 и 689 — сколько единиц в этом числе?10110

Ответов: 3

Информатика 15.10.2023 16:43 6 Кварцхава Константин

Помогите!Изобразить с помощью кругов Эйлера: птица, воробей, перелиная птица, ласточка, аист.Спасибо

Ответов: 2

Информатика 15.10.2023 14:59 4 Baidullina Kamila

В каких единицах измеряется скорость процессора?

Ответов: 3

Информатика 15.10.2023 13:51 31 Гулоян Карен

Палиндромом называется строка, которая одинаково читается как слева направо, так и справа налево.

Ответов: 2

Информатика 15.10.2023 12:40 22 Смирнов Евгений

Из слова электрофотополупроводник составить другие

Ответов: 2

Что такое теория графов и что такое граф?

Теория графов — один из обширнейших разделов дискретной математики, широко применяется
в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических
цепей, коммуникации, психологии, психологии, социологии, лингвистике, других областях знаний. Теория графов систематически
и последовательно изучает свойства графов, о которых можно сказать, что они состоят из множеств точек и
множеств линий, отображающих связи между этими точками. Основателем теории графов считается Леонард
Эйлер (1707-1882), решивший в 1736 году известную в то время задачу о кёнигсбергских мостах.

Графы строят для того, чтобы отобразить отношения на множествах.
Пусть, например, множество —
множество людей, а каждый элемент будет отображён в виде точки

Множество —
множество связок (прямых, дуг, отрезков — пока не важно). На множестве A задано отношение
знакомства между людьми из этого множества

Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
Естественно, число знакомых у одних людей может отличаться от числа знакомых у других людей, а некоторые
вполне могут и не быть ни с кем знакомы (такие элементы будут точками, не соединёнными ни с одной другой). Вот и получился граф!

То, что мы сначала назвали «точками», следует называть вершинами графа, а то, что
называли «связками» — рёбрами графа.

Теория графов не учитывает конкретную природу множеств A и B. Существует
большое количество самых разных конкретных задач, при решении которых можно временно забыть о специфическом
содержании множеств и их элементов

Эта специфика никак не сказывается на ходе решения задачи, независимо
от её трудности! Например, при решении вопроса о том, можно ли из точки a добраться до
точки e, двигаясь только по соединяющим точки линиям, неважно, имеем ли мы дело с людьми,
городами, числами и т.д. Но, когда задача решена, мы получаем решение, верное для любого содержания,
которое было смоделировано в виде графа

Не удивительно поэтому, что теория графов — один из самых
востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может
обсудить с собеседником и вопросы любви, и вопросы музыки или спорта, и вопросы решения различных задач,
причем делает это без всякого перехода (переключения), без которого в подобных случаях не обойтись человеку.

А теперь строгие математические определения графа.

Определение 1. Графом называется система объектов произвольной
природы (вершин) и связок (рёбер), соединяющих некоторые пары этих объектов.

Определение 2. Пусть – (непустое) множество вершин, элементы – вершины.
Граф с множеством вершин есть некоторое
cемейство пар вида: , где , указывающих,
какие вершины остаются соединёнными. Каждая пара — ребро графа.
Множество — множество рёбер графа. Вершины и – концевые точки ребра .

Графы как структура данных. Широким применением теории графов в
компьютерных науках и информационных технологиях обусловлено добавлением к вышеизложенным определениям
понятия графа как структуры данных. В компьютерных науках и информационных технологиях граф определяется
как нелинейная структура данных. Что же тогда — линейная структура данных и чем от них отличаются графы?
Линейные структуры данных характеризуются тем, что связывают элементы отношениями типа «простого соседства».
Линейными структурами данных являются, например, массивы, таблицы, списки, очереди, стеки, строки. В
противоположность им нелинейные структуры данных — такие, в которых элементы располагаются на различных
уровнях иерархии и подразделяются на три вида: исходные, порождённые и подобные. Итак, граф — нелинейная
структура данных.

Слово граф греческого происхождения, от слов «пишу», «описываю». Из начала этой статьи
известно, что именно описывает граф: описывает он отношения. То есть, любой граф описывает отношения. И
наоборот: любое отношение можно описать в виде графа.

Что такое граф, классификация графов, реализация на C++

Граф – совокупность точек, соединенных линиями. Точки называются вершинами, или узлами, а линии – ребрами, или дугами.

Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер.

Граф, содержащий ребра между всеми парами вершин, является полным.

Встречаются такие графы, ребрам которых поставлено в соответствие конкретное числовое значение, они называются взвешенными графами, а это значение – весом ребра.

Когда у ребра оба конца совпадают, т.е. оно выходит из вершины и входит в нее, то такое ребро называется петлей.

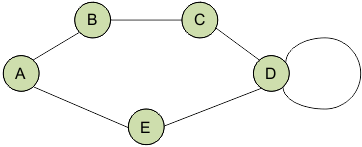
Что такое граф, классификация графов, реализация на C++

Алгоритм поиска в ширину

Алгоритм подобен волне, просматривает ближайшие вершины, потом вершины на расстоянии 2 шагов, 3 и т.д.

1. Создаём очередь вершин для просмотра

2. Создаём список просмотренных вершин

3. Выбираем начальную вершину

   • Упорядочиваем узлы по номеру и берём первую

     либо

   • Выбираем произвольную вершину

4. Добавляем начальную вершину в очередь

5. Пока очередь не пуста

   • Берём элемент из очереди
   • Добавляем его в список просмотренных
   • Ищем все такие узлы, который соединены с текущим
   • Если узел ещё не посещён и ещё не в очереди

Пример кода:

Graph.Nodes = Graph.Nodes.OrderBy(n => n.Id).ToList();

List<Node> visitedNodes = new List<Node>(); // посещённый узлы
Queue<Node> queue = new Queue<Node>(); // очередь узлов к обработке
queue.Enqueue(Graph.Nodes); // добавляем первый узел
// пока очередь не пуста
while (queue.Count > )
{
    Node node = queue.Dequeue(); // достаём первый узел
    visitedNodes.Add(node); // считаем его обработанным
    // ищем все такие узлы, который соединены с текущим
    foreach (var n in Graph.Connections.Select(t => t.GetPairedNode(node)).Where(n => n != null).OrderBy(n=>n.Id))
    {
        // если узел ещё не посещён и ещё не в очереди
        if (!visitedNodes.Contains(n) && !queue.Contains(n))
        {
            node.Children.Add(n); // добавляем дочерний узел
            n.Parent = node; // устанавливаем родительский узел
            queue.Enqueue(n); // добавляем узел в очередь обработки
        }
    }
}

Основные определения

Пусть 𝑉={𝑣1,𝑣2,…,𝑣𝑛} – множество.

Объект вида (𝑣𝑖,𝑣𝑗)называется парой элементов множества V.

Пусть E–множество: 𝐸={𝑒1,𝑒2,…,𝑒𝑚}, элементы которого являются парами вершин: 𝑒1=(𝑣𝑖,𝑣𝑗),𝑒2=(𝑣𝑘,𝑣𝑙),𝑒3=(𝑣𝑘,𝑣𝑙),𝑒4=(𝑣𝑧,𝑣𝑧),

Пара (𝑉,𝐸) называется графом и обозначается 𝐺=(𝑉,𝐸)

Элемент множества 𝑉 называется вершиной графа.

Запись 𝑣𝑖∈𝑉 обозначает, что 𝑣𝑖 является вершиной графа 𝐺=(𝑉,𝐸).

Множество 𝑉 – множество вершин.

Элемент набора 𝐸 называется ребром графа. Запись 𝑒𝑗∈𝐸 обозначает, что 𝑒𝑗 является ребром графа 𝐺=(𝑉,𝐸). Набор 𝐸-набор ребер.

Если все пары в 𝐸 неупорядоченные ((𝑢,𝑣)=(𝑣,𝑢)={𝑢,𝑣}), то граф 𝐺 называется неориентированным.

Если каждая пара в 𝐸 упорядочена ((𝑢,𝑣)≠(𝑣,𝑢)), то граф 𝐺 называется ориентированным графом, или орграфом.

Для оргафов используют обозначение G⃗=(V⃗,E⃗). Элементы E⃗ называются ориентированными ребрами, или дугами, элементы V ⃗ –узлами.

Геометрическая реализация (геометрическая интерпретация) – его изображение на плоскости.

Каждой вершине графа сопоставляется точка, а каждому ребру, т.е. паре вершин – непрерывная не самопересекающаяся кривая, соединяющая эти вершины.

В случае ориентированного графа на кривой указывают направление от начальной вершины дуги к конечной.

Если в множестве 𝐸 есть несколько ребер, заданных одной и той же парой (𝑣,𝑢) называется кратным ребром.

Количество вхождений ребра – его кратность.

Если в множество 𝐸 входит ребро, заданное парой(𝑣,𝑣), то такое ребро пара называется петлей.

Псевдограф – допускаются петли и кратные ребра.
Мультиграф – допускаются только кратные ребра.
Простой граф – в графе нет ни петель, ни кратных ребер.

Если 𝑒=(𝑢,𝑣) – ребро графа 𝐺, то вершины 𝑢 и 𝑣 называются смежными (соседними) или концами ребра 𝑒.

В случае ориентированного графа для дуги 𝑒⃗= (𝑢,𝑣⃗⃗) вершина 𝑢–начальная, вершина 𝑣–конечная.

Также говорят, что дуга 𝑒⃗ исходит из вершины 𝑢 и заходит в вершину 𝑣.

Как в случае ориентированного, так и в случае неориентированного ребра говорят, что ребро 𝑒 (дуга 𝑒⃗) инцидентно вершинам 𝑢 и 𝑣,
а также, что вершины 𝑢 и 𝑣 инцидентны ребру 𝑒 (дуге 𝑒⃗).

Степень вершины (локальная степень вершины) – количество ребер, инцидентных ей. Договоримся петлю учитывать дважды.

Вершина, не инцидентная никакому ребру, называется изолированной.

Граф называется конечным, если число его ребер конечно.

При таком определении конечный граф может иметь бесконечное число вершин, но все они, кроме конечного числа, изолированные.

Теорема. В конечном графе сумма степеней вершин равна удвоенному количеству ребер.

Теорема остается справедливой и при наличии петель, если только в степенях вершин считать их дважды.

• Следствие 1. В конечном графе количество ребер равно полусумме степеней вершин.
• Следствие 2 (лемма о рукопожатиях). В конечном графе число вершин нечетной степени четно.
  (Количество человек, совершивших нечетное число рукопожатий, четно.)

Полный граф — простой неориентированный граф с 𝑛 вершинами и обозначается 𝐾𝑛, если в нем любые две различные вершины смежны.

Количество ребер в 𝐾𝑛. Степень каждой вершины графа 𝐾𝑛 равна (𝑛−1), а количество ребер равно полусумме степеней вершин, то есть 𝑛(𝑛−1) / 2=𝐶2𝑛.

В теории графов классическим способом представления графа служит матрица инциденций (инцидентностей).

• Матрицы инциденций неориентированных графов

• Матрицы инциденций ориентированных графов

• Матрицы смежности графов.

Способы представления графа

Граф может быть представлен (сохранен) несколькими способами:

• матрица смежности;
• матрица инцидентности;
• список смежности (инцидентности);
• список ребер.

Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Размер массива зависит от количества вершин и/или ребер в конкретном графе.

Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1.

Число строк матрицы смежности равно числу столбцов и соответствует количеству вершин графа.

•  – соответствует отсутствию ребра,
• 1 – соответствует наличию ребра.

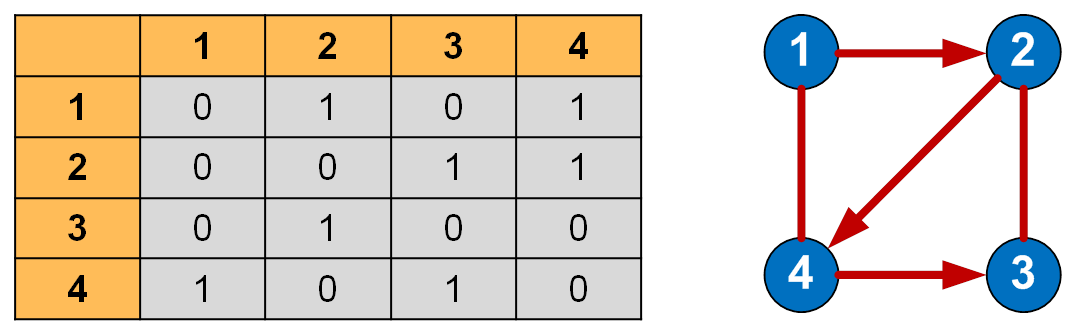
Матрица смежности графа

Когда из одной вершины в другую проход свободен (имеется ребро), в ячейку заносится 1, иначе – 0. Все элементы на главной диагонали равны 0 если граф не имеет петель.

Матрица инцидентности (инциденции) графа — это матрица, количество строк в которой соответствует числу вершин, а количество столбцов – числу рёбер. В ней указываются связи между инцидентными элементами графа (ребро(дуга) и вершина).

В неориентированном графе если вершина инцидентна ребру то соответствующий элемент равен 1, в противном случае элемент равен 0.

В ориентированном графе если ребро выходит из вершины, то соответствующий элемент равен 1, если ребро входит в вершину, то соответствующий элемент равен -1, если ребро отсутствует, то элемент равен 0.

Матрица инцидентности для своего представления требует нумерации рёбер, что не всегда удобно.

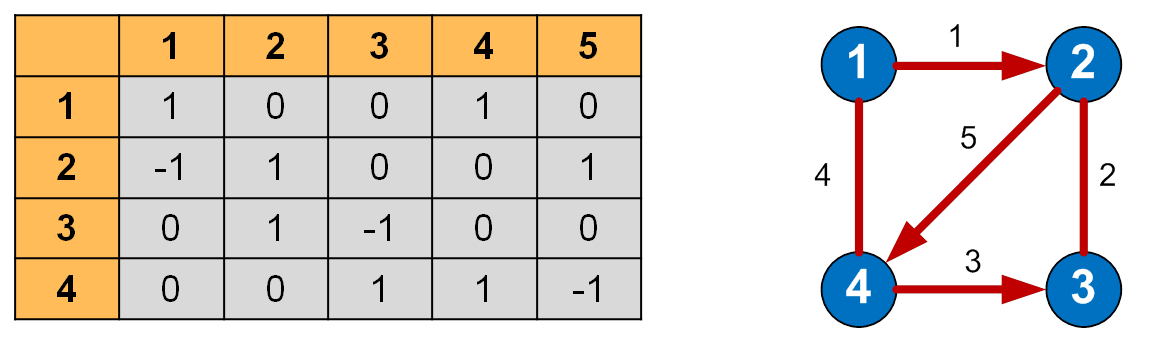
Матрица инцидентности (инциденции) графа

Список смежности (инцидентности)
Если количество ребер графа по сравнению с количеством вершин невелико, то значения большинства элементов матрицы смежности будут равны 0. При этом использование данного метода нецелесообразно. Для подобных графов имеются более оптимальные способы их представления.

По отношению к памяти списки смежности менее требовательны, чем матрицы смежности. Такой список можно представить в виде таблицы, столбцов в которой – 2, а строк — не больше, чем вершин в графе.
В каждой строке в первом столбце указана вершина выхода, а во втором столбце – список вершин, в которые входят ребра из текущей вершины.

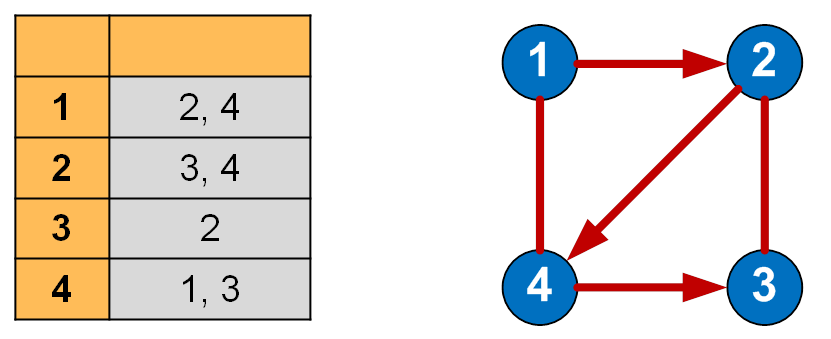
Список смежности (инцидентности)

Преимущества списка смежности:

• Рациональное использование памяти.
• Позволяет быстро перебирать соседей вершины.
• Позволяет проверять наличие ребра и удалять его.

Недостатки списка смежности:

• При работе с насыщенными графами (с большим количеством рёбер) скорости может не хватать.
• Нет быстрого способа проверить, существует ли ребро между двумя вершинами.
• Количество вершин графа должно быть известно заранее.
• Для взвешенных графов приходится хранить список, элементы которого должны содержать два значащих поля, что усложняет код:
  • номер вершины, с которой соединяется текущая;
  • вес ребра.

Список рёбер
В списке рёбер в каждой строке записываются две смежные вершины и вес соединяющего их ребра (для взвешенного графа).
Количество строк в списке ребер всегда должно быть равно величине, получающейся в результате сложения ориентированных рёбер с удвоенным количеством неориентированных рёбер.

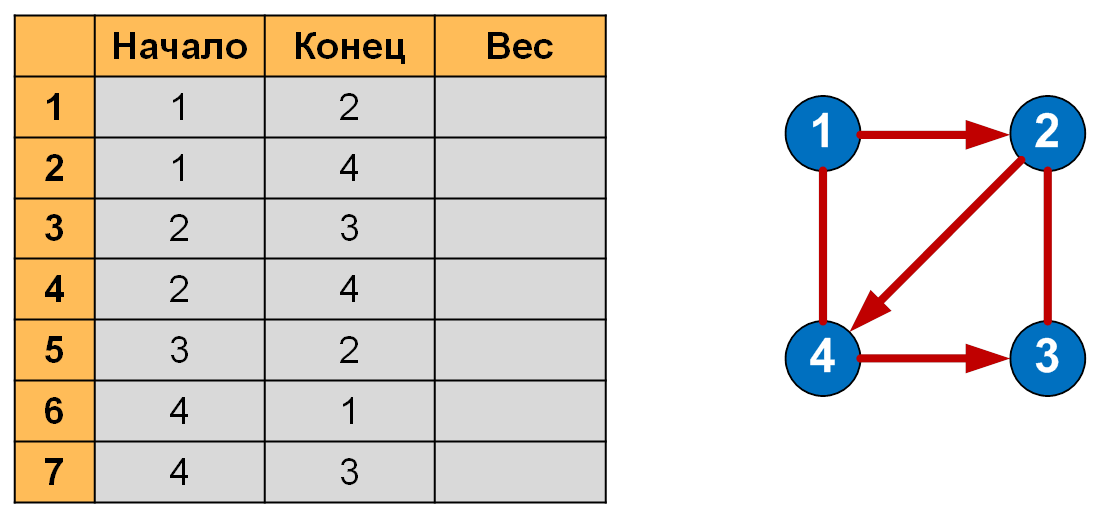
Список рёбер

Какой способ представления графа лучше? Ответ зависит от отношения между числом вершин и числом рёбер. Число ребер может быть довольно малым (такого же порядка, как и количество вершин) или довольно большим (если граф является полным). Графы с большим числом рёбер называют плотными, с малым — разреженными. Плотные графы удобнее хранить в виде матрицы смежности, разреженные — в виде списка смежности.