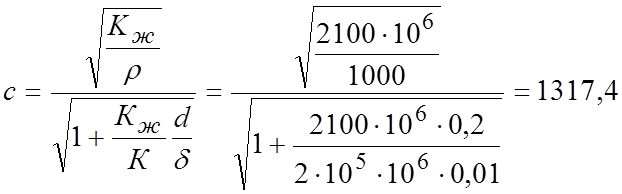Движение жидкости

Основные уравнения равновесия и движения жидкостей

Силы, действующие в жидкости, обычно разделяют на массовые (объемные) и поверхностные. Примером массовых сил может служить сила тяжести. Обозначим — объемную плотность массовых сил. Поверхностные силы — это силы, которые действуют на каждый объем жидкости, благодаря нормальным и касательным напряжениям, действующим на его поверхности со стороны соседних частей жидкости.

Основным уравнением гидростатики является выражение:

Уравнение (4) показывает, что при равновесии жидкости плотность силы, действующая на единицу объема жидкости ( есть градиент скалярной функции. Это необходимое и достаточное условие консервативности плотности силы . Получается, что для равновесия жидкости надо, чтобы поле сил, в котором находится жидкость, было консервативным. В неконсервативных силовых полях равновесие не возможно.

В координатной форме формулу (4) запишем как:

Основным уравнением гидродинамики идеальной жидкости является выражение:

где ускорение жидкости в рассматриваемой точке. Уравнение (6) называется уравнением Эйлера.

Уравнением Бернулли получено швейцарским физиком Д. Бернулли в 1738 г. Это выражение закона сохранения энергии относительно установившегося течения идеальной жидкости:

где — статическое давление — давление жидкости на поверхности тела, которое она обтекает; — динамическое давление; — гидростатическое давление; — высота столба жидкости.

Графически движение жидкости изображают при помощи линий тока. Их проводят так, что касательные к ним совпадают по направлению с вектором скорости в соответствующих точках пространства. Жидкость, ограниченную линиями тока называют трубкой тока. При стационарном течении жидкости форма и расположение линий тока не изменяется.

Движение несжимаемой жидкости подчиняется уравнению неразрывности, которое записывают как:

И — сечения трубки тока.

7.2. Примеры решения задач

Пример 7.1. Определить
время закрытия задвижки, установленной на свободном конце стального водопровода
диаметром м, длиной м
с толщиной стенки мм, при условии, чтобы
максимальное повышение давления в водопроводе было в три раза меньше, чем при
мгновенном закрытии задвижки. Через сколько времени после мгновенного закрытия
задвижки повышение давления распространится до сечения, находящегося на
расстоянии от задвижки ?

Решение:

Время закрытия задвижки находим из уравнения (7.3).
Согласно условию задачи, максимальное повышение давления в водопроводе должно
быть в три раза меньше, чем при мгновенном закрытии задвижки, т.е. , где —
приращение давления при прямом гидравлическом ударе. Величину определяем по формуле Жуковского
(7.2).

Таким образом, получим

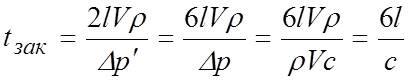Скорость распространения ударной волны найдем из
уравнения (7.4)

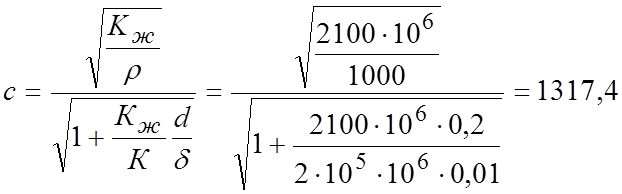м/с.

Следовательно, время закрытия задвижки

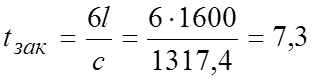с.

Найдем время, через которое повышение давления после
мгновенного закрытия задвижки распространится до сечения, находящегося на расстоянии
от задвижки

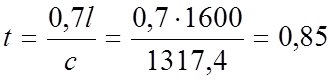с.

Ответ: с; с.

Задачи гидродинамики

Жидкость, находящаяся в движении обычно характеризуется при помощи двух параметров: скорости течения () и гидродинамического давления (). Следовательно, к основным задачам гидродинамики относят определения этих параметров при известной системе действующих внешних сил.

В процессе движения жидкости и способны изменяться в зависимости от времени и точки в пространстве. При этом выделяют два типа движения жидкости установившееся и неустановившееся.

Движение, при котором и являются постоянными во времени для любой точки жидкости в пространстве и являются функция координат, называют установившимся. При неустановившемся течении скорость и давление являются функциями и от времени и от координат.

В гидродинамике используют понятие жидкой частицы. Это условно выделяемый элементарный объем жидкости, изменением формы которого можно пренебречь. Частица жидкости при своем движении описывает кривую, которая носит название траектории движения.

Потоком жидкости считают перемещающуюся массу жидкости, которая полностью или частично ограничена поверхностями. Эти поверхности могут образовываться самой жидкостью на фазовой границе или быть твердыми. Границы потоков — это стенки трубы, канала, поверхность, которую жидкость обтекает, открытая поверхность жидкости.

Небольшая сжимаемость жидкости позволяет во многих случаях полностью пренебречь изменением ее объема. Тогда говорят о несжимаемой жидкости. Это идеализация, которую часто используют. Говорят, что несжимаемая жидкость — предельный случай сжимаемой жидкости, когда для получения бесконечно больших давлений, достаточно бесконечно малых сжатий.

Жидкость, в которой при любом ее движении не возникают силы внутреннего трения, называют идеальной. Иначе говоря, в идеальной жидкости существуют только силы нормального давления, которые однозначно определяются степенью сжатия и температурой жидкости. Модель идеальной жидкости используют тогда, когда скорости изменения деформаций в жидкости малы.

Физическая величина, которая определяется нормальной силой, с которой жидкость действует на единицу площади поверхности, называют давлением ():

Давление при равновесии жидкости подчиняется закону Паскаля:

Давление в любой точке покоящейся жидкости одинаково во всех направлениях. Давление одинаково передается во всем объеме, которое жидкость занимает.

Сила давления на нижние слои жидкости больше, чем на верхние. Вследствие этого на тело, погруженное в жидкость (газ) действует выталкивающая сила, называемая силой Архимеда ():

где — плотность жидкости; — объем тела, погруженного в жидкость.

В состоянии равновесия жидкости (газа) давление () меняется в зависимости от плотности ( и температуры () и однозначно определено ими. Соотношение:

в состоянии равновесия называют уравнением состояния.

Скорости течения воды и распределение их по живому сечению

Скорости течения в реках неодинаковы в различных точках потока: они изменяются и по глубине и по ширине живого сечения. На каждой отдельно взятой вертикали наименьшие скорости наблюдаются у дна, что связано с влиянием шероховатости русла. От дна к поверхности нарастание скорости сначала происходит быстро, а затем замедляется, и максимум в открытых потоках достигается у поверхности или на расстоянии 0,2H от поверхности. Кривые изменения скоростей по вертикали называются годографами или эпюрами скоростей (рис. 66). На распределение скоростей по вертикали большое влияние оказывают неровности в рельефе дна, ледяной покров, ветер и водная растительность. При наличии на дне неровностей (возвышения, валуны) скорости в потоке перед препятствием резко уменьшаются ко дну. Уменьшаются скорости в придонном слое при развитии водной растительности, значительно повышающей шероховатость дна русла. Зимой подо льдом, особенно при наличии шуги, под влиянием добавочного трения о шероховатую нижнюю поверхность льда скорости малы. Максимум скорости смещается к середине глубины и иногда расположен ближе ко дну. Ветер, дующий в направлении течения, увеличивает скорость у поверхности. При обратном соотношении направления ветра и течения скорости у поверхности уменьшаются, а положение максимума смещается на большую глубину по сравнению с его положением в безветренную погоду.

По ширине потока скорости как поверхностная, так и средняя на вертикалях меняются довольно плавно, в основном повторяя распределение глубин в живом сечении: у берегов скорость меньше, в центре потока она наибольшая. Линия, соединяющая точки на поверхности реки с наибольшими скоростями, называется стрежнем. Знание положения стрежня имеет большое значение при использовании рек для целей водного транспорта и лесосплава. Наглядное представление о распределении скоростей в живом сечении можно получить построением изотах — линий, соединяющих в живом сечении точки с одинаковыми скоростями (рис. 67). Область максимальных скоростей расположена обычно на некоторой глубине от поверхности. Линия, соединяющая по длине потока точки отдельных живых сечений с наибольшими скоростями, называется динамической осью потока.

Рис. 66. Эпюры скоростей.
а — открытое русло, б — перед препятствием, в — ледяной покров, г — скопление шуги.

Средняя скорость на вертикали вычисляется делением площади эпюры скоростей на глубину вертикали или при наличии измеренных скоростей в характерных точках по глубине (V_ПОВ, V_0,2, V_0,6, V_0,8, V_ДОН) по одной из эмпирических формул, например

Движение установившееся и неустановившееся. Понятие о местной осредненной скорости

Движение установившееся и неустановившееся. Понятие о местной осредненной скорости. В зависимости от условий, вызывающих движение жидкости Это движение является стационарным (неподвижным) g Или нестационарный (нестационарный Лама послужит примером стабильного движения. Трубопроводный поток. Тем не менее, уровень жидкости ГНИ 13 бак (рис. 7-1) остается неизменным. Стационарный поток характеризуется постоянным полем Само движение-это скорость пространства, занимаемого потоком Частицы могут быть неравномерными.

Предмет гидравлика

Если движение трубопровода становится неустойчивым Уровень жидкости в баке меняется. Следовательно Неустойчивое движение характеризуется за пределами пространства Поле скорости, которое извлекается потоком и изменяется с течением времени. Дай Общее определение устойчивых понятий Гоша упражнение. Рассмотрим конкретный поток (рис. 7-3) и выберем в пространстве В собственность занимаемого потоком, любой точки y и r * Скорость и давление частиц, проходящих в разное время Через точки пространства а, будут разные, такие движения Это называется неустановившимся.

Ламинарное и турбулентное движение.

Скорость (и давление, меняя во времени с черточкой идут-пункты Он также изменяется при перемещении частиц жидкости от 1 частицы Еще одно условие. Аналитически, это Движение скорости и гидродинамического давления Координат функции точек x y и r в занимаемой площади Поток и время В отличие от неудержимого, в стабильном движении Скорость движения и гидродинамическое давление в данной точке Пространство постоянно. То есть она тоже не меняется во времени. Размер и направление частиц Жидкость, которая попадает в «другую нагрузку» в точке пространства a.

Имеют одинаковую скорость и гидродинамическое давление (Рис. 7-4). Аналитически, это было установлено Скорость движения и гидродинамическое давление Он работает только для x, y и т. д. Переменные x, y1 g и i называются переменными Эйлера Как изучать выраженные гидродинамические величины В виде функциональной зависимости переменных Эйлера 1. Он называется методом Эйлера. ух. .Постоянная скорость и гидродинамическое давление Изменение при движении, ми в точке погружения пространства Жидкие частицы из одного положения в другое .

Инвариантность поля скоростей в установившемся потоке Это выражается математически следующим образом .Экспериментальные исследования показали, что турбулентность Движение всегда преходяще только движение Мы шьем .На рис . 1 7-5 показана схема изменения осевой составляющей Скорость в точке турбулентности .Жидкость Оно пропускает от резервуара в трубопровод, и жидкостный уровень Тор оставался неизменным .Из рисунка Поле скоростей турбулентности изменяется .Несмотря на Кажущаяся случайность изменения скорости в какой-то момент Компоненты в нем изменяются вокруг определенного среднего времени О чтении .

Средняя скорость в живом сечении. Формула Шези

Для вычисления средней скорости потока при отсутствии непосредственных измерений широко применяется формула Шези. Она имеет следующий вид:

_ср

Величина коэффициента С не является величиной постоянной. Она зависит от глубины и шероховатости русла. Для определения С существует несколько эмпирических формул. Приведем две из них:

формула Манинга

формула Н. Н. Павловского
где n — коэффициент шероховатости, находится по специальным таблицам М. Ф. Срибного. Переменный показатель в формуле Павловского определяется зависимостью.

Из формулы Шези видно, что скорость потока растет с увеличением гидравлического радиуса или средней глубины. Это происходит потому, что с увеличением глубины ослабевает влияние шероховатости дна на величину скорости в отдельных точках вертикали и тем самым уменьшается площадь на эпюре скоростей, занятая малыми скоростями. Увеличение гидравлического радиуса приводит и к увеличению коэффициента С. Из формулы Шези следует, что скорость потока растет с увеличением уклона, но этот рост при турбулентном движении выражен в меньшей мере, чем при ламинарном.

Поток жидкости и его параметры

Поток жидкости характеризуется такими параметрами как площадь живого сечения S, расход жидкости Q(G), средняя скорость движения v.

Живое сечение потока — это сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.

Векторы скорости частиц имеют некоторое расхождение в потоке жидкости.

Живым сечением потока жидкости называется сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.

Поэтому живое сечение потока — криволинейная плоскость (рис. а, линия I—I) В виду незначительного расхождения векторов скорости в гидродинамике за живое сечение принимается плоскость, расположенная перпендикулярно скорости движения жидкости в средней точке потока.

Расход жидкости — это количество жидкости, протекающей через живое сечение потока в единицу времени. Расход может определяться в массовых долях G и объемных Q.

Средняя скорость движения жидкости — это средняя скорость частиц в живом сечении потока.

Если в живом сечении потока, движущегося, например, в трубе, построить векторы скорости частиц и соединить концы этих векторов, то получится график изменения скоростей (эпюра скоростей).

Если площадь такой эпюры разделить на диаметр данной трубы, то получится значение средней скорости движения жидкости в данном сечении:

Объемный расход жидкости рассчитывается по формуле:

Параметры потока жидкости определяют характер движения жидкости. При этом оно может быть установившимся и неустановившимся, равномерным и неравномерным, неразрывным и кавитационным, ламинарным и турбулентным.

Если параметры потока жидкости не изменяются во времени, то ее движение называется установившимся.

Равномерным называется движение, при котором параметры потока не изменяются по длине трубопровода или канала. Например, движение жидкости по трубе постоянного диаметра является равномерным.

Неразрывным называется движение жидкости, при котором она перемещается сплошным потоком, заполняющим весь объем трубопровода.

Отрыв потока от стенок трубопровода или от обтекаемого предмета приводит к возникновению кавитации.

Кавитацией называется образование в жидкости пустот, заполненных газом, паром или их смесью.

Кавитация возникает в результате местного уменьшения давления ниже критического значения pкр при данной температуре (для воды ркр= 101,3 кПа при Т= 373 К или ркр= 12,18 кПа при Т= 323 К и т. д.). При попадании таких пузырьков в зону, где давление выше критического, в эти пустоты устремляются частицы жидкости, что приводит к резкому возрастанию давления и температуры. Поэтому кавитация неблагоприятно отражается на работе гидротурбин, жидкостных насосов и других элементов гидравлических устройств.

Ламинарное движение — это упорядоченное движение жидкости без перемешивания между ее соседними слоями. При ламинарном течении скорость и силы инерции, как правило, невелики, а силы трения значительны. При увеличении скорости до некоторого порогового значения ламинарный режим течения переходит в турбулентный.

Турбулентное движение — это течение жидкости, при котором ее частицы совершают неустановившееся беспорядочное движение по сложным траекториям. При турбулентном течении скорость жидкости и ее давление в каждой точке потока хаотически изменяется, при этом происходит интенсивное перемешивание движущейся жидкости.

Для определения режима движения жидкости существуют условия, согласно которым скорость потока может быть больше или меньше той критической скорости, когда ламинарное движение переходит в турбулентное и наоборот.

Однако установлен и более универсальный критерий, который называют критерием или числом Рейнольдса:

Опытами было установлено, что в момент перехода ламинарного режима движения жидкости в турбулентный Re = 2320.

Число Рейнольдса, при котором ламинарный режим переходит в турбулентный, называется критическим. Следовательно, при Re 2320 — турбулентное. Отсюда критическая скорость для любой жидкости:

Примеры решения задач

ПРИМЕР 1

Задание

Запишите уравнение равновесия жидкости в случаях: а) когда массовых сил нет; б) жидкость находится в поле тяжести. Поясните, что следует из записанных уравнений?

Решение

а) Если массовые силы равны нулю (), то уравнение гидростатики запишем как:

Следовательно, при равновесии давление одинаково по всему объему жидкости.

б) Если жидкость находится в поле тяжести, то . Направим ось Z вертикально вверх. Тогда основные уравнения равновесия можно записать как:

Из уравнений (1.2) следует, что при механическом равновесии давление не зависит от координат x, y. Оно остается постоянным в любой горизонтальной плоскости . Горизонтальные плоскости являются плоскостями равного давления. Так, свободная поверхность жидкости является горизонтальной, так как она находится под постоянным атмосферным давлением. Из третьего уравнения системы (1.2) следует, что для механического равновесия надо, чтобы являлось функцией только от . Если зависимостью ускорения свободного падения от широты и долготы пренебречь, то плотность изменяется только в зависимости от высоты. А из уравнения состояния:

следует, что при механическом равновесии давление, температура и плотность жидкости зависят только от и не могу зависеть от .

Поток жидкости через поверхность

Как и при изучении криволинейных интегралов, начнём с физической задачи. Пусть через объём $\mathbf > $ течёт поток жидкости, имеющий скорость $\bar (M)$ в точке $\mathbf > $. Пусть в $\mathbf > $ размещена проницаемая поверхность $\sigma $. Требуется найти количество $\Pi $ жидкости, протекающей через $\sigma $ за единицу времени. В дальнейшем мы будем называть это количество потоком через поверхность.

В случае, когда $\sigma $ — ограниченная плоская область и $\bar (M)= \overline $, решение очевидно. Это количество равно объёму, ограниченному цилиндрической поверхностью с основанием $\sigma $ и боковой стороной $\bar (M)$. Площадь основания объёма равна $\sigma $ , высота $h=\mbox _ > \bar =\vert \bar \vert \cos \varphi =\bar \cdot \bar $, т.е. равна скалярному произведению вектора скорости на единичный вектор нормали. Итак, $\Pi =\bar \bar \sigma $. Заметим, что изобразив на рисунке единичный вектор нормали, мы ввели на поверхности ориентацию. Так, применительно к рисунку справа, мы выбрали верхнюю сторону поверхности; если бы выбрали противоположную нормаль, поток изменил бы знак.

Возможны два способа представления этой величины.

Обозначив $f=(\bar \cdot \bar )$, получим $\prod = f\cdot\sigma$
Если в некоторой координатной системе $\bar (M)$ имеет координаты $\mathbf > $, $\mathbf > $, $\mathbf > $, единичный вектор $\bar (M)$ имеет координаты — направляющие косинусы $\cos \alpha ,\cos \beta ,\cos \gamma $, то $\Pi =\bar \bar \sigma =(P\cos \alpha +Q\cos \beta +R\cos \gamma )\sigma =P(\cos \alpha \cdot \sigma )+Q(\cos \beta \cdot \sigma )+R(\cos \gamma \cdot \sigma )$.

Чему равно произведение $\cos \gamma \cdot \sigma $? Произведение $\vert \cos \gamma \vert \cdot \sigma $ равно площади $s(D_ )$ проекции $D_ $ поверхности $\sigma $ на плоскость $\mathbf > $ .

Следовательно, $\cos \gamma \cdot \sigma $ равно $s(D_ )$, если $\cos \gamma \geqslant 0$ (M)$ на орт $\bar $ оси $\mathbf > $ положительна > . Этот случай соответствует верхнему рисунка.

Соответственно, $\cos \gamma \cdot \sigma $ равно $-s(D_ )$, если $\cos \gamma Огравление $\Rightarrow $

Скорость течения горных и равнинных рек

Течение равнинных рек значительно более спокойное, чем горных. Водная поверхность равнинных рек сравнительно ровная. Препятствия обтекаются потоком спокойно, кривая подпора, возникающего перед препятствием, плавно сопрягается с водной поверхностью вышерасположенного участка.

Горные реки отличаются крайней неровностью водной поверхности (пенистые гребни, взбросы, провалы). Взбросы возникают перед препятствием (нагромождением валунов на дне русла) или при резком уменьшении уклона дна. Взброс воды в гидравлике носит название гидравлического (водного) прыжка. Его можно рассматривать как одиночную волну, появившуюся на водной поверхности перед препятствием. Скорость распространения одиночной волны на поверхности, как известно, c = , где g — ускорение силы тяжести, H — глубина.

Если средняя скорость течения v_ср потока оказывается равной скорости распространения волны или превышает ее, то образующаяся у препятствия волна не может распространиться вверх по течению и останавливается вблизи места ее возбуждения. Формируется остановившаяся волна перемещения.

Пусть v_ср = c. Подставляя в это равенство значение из предыдущей формулы, получим v_ср = , или

Левая часть этого равенства известна как число Фруда (Fr). Это число позволяет оценить условия существования бурного или спокойного режима течения: при Fr 1 — бурный режим.

Таким образом, между характером течения, глубиной, скоростью, а следовательно, и уклоном существуют следующие соотношения: с увеличением уклона и скорости и уменьшением глубины при данном расходе течение становится более бурным; с уменьшением уклона и скорости и увеличением глубины при данном расходе течение приобретает более спокойный характер.

Горные реки характеризуются, как правило, бурным течением, равнинные реки имеют спокойный режим течения. Бурный режим течения может быть и на порожистых участках равнинных рек. Переход к бурному течению резко усиливает турбулентность потока.

Неустановившееся движение — жидкость

Неустановившееся движение жидкости в напорных системах требует в некоторых случаях учета упругих свойств как самой жидкости, так и стенок трубопроводов.

Неустановившееся движение жидкости — движение, при котором давление и скорость ее в каждой точке пространства изменяются с течением времени.

Неустановившееся движение жидкости возникло из-за отключения сосредоточенного отбора.

Неустановившееся движение жидкости в настоящее время является основным видом движения нефтей и нефтепродуктов по магистральным трубопроводам.

График подачи трехплунжерного насоса.

Неустановившееся движение жидкости в трубопроводе при значительной его длине вызывает нежелательные инерционные явления. В начале хода нагнетания жидкость, находящаяся в напорном трубопроводе, должна быть ускорена. Для преодоления сил инерции этой жидкости необходим избыток давления в рабочей камере. Аналогично в начале хода всасывания для преодоления сил инерции жидкости, находящейся во всасывающем трубопроводе, необходимо создать в рабочей камере значительно большее разрежение, чем это требовалось бы при равномерной подаче.

Рассмотрим неустановившееся движение жидкости, при котором скорости и давления в каждой точке потока меняются с течением времени.

Если неустановившееся движение жидкости возникает вследствие гидравлических возмущений ( включение или отключение насосав, гидравлические удары), то переходный процесс можно разделить на два этапа. На первом из них продолжительностью не более нескольких десятков минут происходит существенное изменение скорости потока и, давления -, а распределение температур остается приблизительно постоянным. На втором этапе продолжительностью 1 сут и более происходят квазистационарное, медленное изменение температуры и связанное с ним постепенное изменение давления и расхода. Если неустановившийся режим возникает только вследствие изменения параметров работы тепловых станций, то первый этап переходного процесса отсутствует.

Рассмотрим неустановившееся движение жидкости, при которой скорости и давления в каждой точке потока меняются с течением времени.

Различают напорное и безнапорное неустановившееся движение жидкости, одномерное, двухмерное и пространственное неустановившееся движение.

Исследования неустановившегося движения жидкости в гидравлических магистралях, необходимость в которых все более возрастает в различных областях техники, включает и задачу определения изменения объема участков магистрали при изменении давления рабочей жидкости в ней. Полученные до настоящего времени решения этой задачи для участков гидро-маг.

Задачи неустановившегося движения жидкости и газа в пласте решаются методами математической физики. Для этого составляются и затем интегрируются дифференциальные уравнения. Чтобы вывести дифференциальные уравнения фильтрации в пористой среде, заключающей в себе движущийся флюид ( жидкость, газ), выделяется бесконечно малый элемент пласта и рассматриваются изменения массы, импульса и энергии, происходящие в этом элементе за бесконечно малый промежуток времени. При этом используются законы сохранения массы, импульса и энергии, а также результаты лабораторного или промыслового экспериментального изучения свойств и поведения флюидов и свойств пористой среды с изменением термобарических условий.

Вопросы неустановившегося движения жидкости и газа в трубах имеют существенное значение как при проектировании, так и при эксплуатации трубопроводов различного назначения.

Действие усилий на образец пористой среды.