Что такое астрономическая единица

КУМУЛЯЦИЯ И АМБИВАЛЕНТНОСТЬ В СЕМАНТИКЕ МИФОЛОГЕМ (НА ПРИМЕРЕ РЕПРЕЗЕНТАНТА HORSESHOE КОНЦЕПТА SUPERSTITION В АНГЛОСАКСОНСКОЙ КУЛЬТУРЕ)

Статья посвящена исследованию внутренней, «невидимой» структуры репрезентанта horseshoe концепта SUPERSTITION в англосаксонской культуре, отражающей основные категории магического мышления. Новизна настоящего исследования состоит в том, что оно выполнено в рамках теолингвистики, а именно теолингвоконцептологии как ее раздела (Постовалова, 2016). Для анализа языковых репрезентантов исследуемого концепта используется разработанный нами метод анализа онтологических концептов (Степаненко, 2006; Stepanenko, 2015. P. 185-195; Степаненко, 2019. С. 467-488). История подковы уходит корнями в глубокую древность, к дохристианской цивилизации. Как амбивалентный символ она интерпретируется в двух концептуальных системах — языческой и христианской. Астрономический атрибут языческих богинь — полумесяц — был «переведен» на язык христианского богословия с измененной семантикой его символа, благодаря которой евангельское повествование мира трансцендентного передается на язык имманентный. Современная …

Астрономическая единица

В принципе, в масштабах солнечной системы, еще актуальны привычные нам километры и метры, но все же удобнее использовать астрономические единицы.

Одна астрономическая единица (а.е.) соответствует среднему расстоянию от Земли до Солнца или размеру большой полуоси ее орбиты. Это 149 597 870 700 метров.

1 а.е. = 149 597 870 700 м

Восемь астрономических единиц, это минимальное расстояние, на которое сближается Сатурн и Земля. Можете перевести это расстояние в километры, и прикинуть сколько раз придется сделать капиталку двигателя вашего автомобиля намотав на нем такой километраж.

Астрономическая единица по Земным меркам величина, конечно, большая, но все же для измерения расстояний за пределами солнечной системы она будет мелковата. Поэтому идем дальше.

Единицы измерения астрономических расстояний

Одна из основных задач астрономии — узнать расстояние для того или иного небесного тела,

Какие же системы и меры расчета используются в астрономии?

Астрономическая единица (а. е).

Данная единица используется для измерения расстояний внутри нашей Солнечной системы или внутри иных планетных систем. Такая единица равняется радиусу орбиты Земли вокруг Солнца. Или же среднему расстоянию от нашей планеты до Солнца. Таким образом, одна астрономическая единица получается равная примерно 150 000 000 км.

В пользу использования астрономической единицы, в частности, говорит возможность сравнивать измеряемые расстояния с удаленностью Земли от Солнца. Измерения таких больших чисел в километрах неудобно и затруднительно.

Толчком к появлению астрономической единицы послужило открытие того, что Земля обращается вокруг Солнца, и разработка Кеплером законов небесной механики. С помощью расчетов удалось установить точное расстояние от Земли до Солнца и до планет Солнечной системы.

В дальнейшем благодаря развитию науки и техники удалось уточнить расстояния от Земли до Солнца и планет нашей системы.

В 1962 году специалистам удалось измерить при помощи радиолокационных сигналов расстояние от Земли до Солнца. В результате эталоном была принята средняя величина, которая равна 149597870,7 км. С таким значением данное определение и содержится теперь в Международной системе единиц СИ.

Однако, наблюдения показали, что астрономическая единица не является постоянной. Так, выяснилось, что в течении каждых 7 лет длина астрономической единицы увеличивается на метр. Точного объяснения такого увеличения расстояния нет. Однако, наиболее поддерживаемой теорией является идея о том, что причиной является уменьшение массы Солнца из-за воздействия солнечного ветра.

Световой год

Определение 1

Световой год – это единица измерения расстояний в космосе, которая, однако, не является системной и применяется в основном в учебной и популярной литературе по астрономии.

Под световым годом понимается расстояние, которое пройдет луч света за 365,25 земных дня (т. е. за земной год) в вакууме, при этом не луч не должен на себе испытывать воздействие магнитных полей.

Световой год равен 9,46 триллионам километров

В научной практике световой год применяется редко и в основном для выражения расстояний до не особо далеких объектов в космосе. Причиной этого является, то, что при выражении расстояния до далеких галактик в световых годах, число оказывается слишком большим и неудобным в расчетах. Поэтому для подобных расчетов применяется парсек.

Парсек

Определение 2

Парсек – происходит от сокращения «параллакс секунда», и является внесистемной единицей измерения, с помощью которой происходит определение расстояния до очень отдаленных объектов исследования.

Для понимания того, что такое парсек необходимо узнать, что такое параллакс.

Параллакс состоит в том, что при перемещении наблюдателя в процессе наблюдения за двумя отдаленными друг от друга телами, расстояние между данными объектами также меняется.

При наблюдении за звездами параллакс возникает при изменении положения звезды при смещении Земли на один градус её орбиты. Это называется годичный параллакс и измеряется в угловых секундах. В результате если годичный параллакс равен одной угловой секунде, то и расстояние до звезды оценивается в один парсек. Точное число парсека оценивают в 3,0856776•1016 метра или 3,2616 светового года. 1 парсек равен примерно 206 264,8 а. е.

Методы определения расстояний в астрономии

Метод лазерной локации и радиолокации.

Метод лазерной локации заключается в отправлении в сторону объекта наблюдения радиосигнала. После этого объект отражает сигнал и тот возвращается обратно. В результате, время, которое тратится на преодоления расстояния, помогает определить расстояние до цели.
При этом точность радиолокации составляет всего несколько километров.

Лазерная локация предполагает отправку светового луча, который помогает таким же образом определить расстояние до цели, но уже с точностью до долей сантиметра.

Метод тригонометрического параллакса.

Замечание 1

Тригонометрический параллакс является одним из самых простых методов измерения расстояния в космосе. Данный метод основан на школьных знаниях из геометрии.

Итак, рассмотрим метод тригонометрического параллакса.

Начертим отрезок (иначе именуемый базисом) между двумя точками на поверхности Земли. Затем мы выбираем нужный объект на небе, расстояние до которого нам нужно определить, и обозначаем его как вершину получившегося у нас треугольника. Потом мы замеряем углы между начертанным базисом и прямыми, которые были проведены от выбранных точек до нужного нам объекта в небе. А поскольку нам известна сторона и два прилежащих к ней угла треугольника, то можно определить и остальные его элементы.

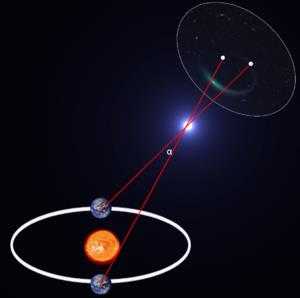Рисунок 1. Тригонометрический параллакс. Автор24 — интернет-биржа студенческих работ

В первое время в роли базиса выступал радиус Земли, однако, впоследствии в качестве базиса стали брать средний радиус орбиты Земли, т. е. астрономическую единицу. Это позволяло узнать расстояние до более отдаленных небесных тел. Угол, который лежал в данном случае напротив базиса называется годичным параллаксом.

Такое измерение расстояние до звезд не очень удобно при исследованиях с Земли. Причиной являются помехи атмосферы. Поэтому определение годичного параллакса для объектов расположенных на расстоянии больше чем в 100 парсек не удавалось.

Выходом стал, в частности, запуск в 1989 год Европейским космическим агентством космического телескопа Hipparcos. Этот телескоп способен определить расстояние до звезд в 1000 парсек.

Итогом стало получение трехмерной карты всех звезд, расположенных вокруг Солнца. А в 2013 году тоже Агентство запустило ещё более точный аппарат – Gaia. Точность данного аппарата в 100 раз лучше прежнего. Это позволяет наблюдать все звезды Млечного Пути.

Метод стандартных свечей.

Замечание 2

Метод стандартных свечей основан на том, что чем дальше от наблюдателя источник света, тем он кажется более тусклым. В результате возможно сравнивать расстояние до нужных звезд с расстояниями до звезд с известными нам мощностями.

При использовании данного метода за основу стандартных свечей берут источники, мощность которых известна исследователям. Таким источником может выступать звезда, температура поверхности и яркость которой известна. Такие расчеты помогают получить общие данные о расстоянии до галактики, в которой эта звезда расположена.

Недостатками такого метода является его сложность и не очень высокая точность.

Уникальные стандартные свечи.

При помощи данного метода удается более точно определить расстояния до звезды, опираясь на характеристики цефеид.

Цефеиды – переменные пульсирующие звезды, которые используются земными астрономами как своеобразные маяки – стандартные свечи. Изучая их физические свойства, астрономам удалось узнать, что цефеиды обладают такой особенностью как период пульсации. Период пульсации и яркость переменных звезд дают возможность узнать светимость и соответственно расстояние до данной звезды.

Рисунок 2. Цефеиды. Автор24 — интернет-биржа студенческих работ

Также в роли уникальных стандартных свечей могут выступать сверхновые, чья светимость известна, а также красные гиганты.

Общепринятая астрономическая единица, как единица измерения

Первыми, кто решил измерить пространство от Земли до ближайшей звезды и узнать параллакс светила, а также сравнить результаты с параллаксом сестры родной планеты, были астрономы Уильям Крабтри и Джереми Хоррокс. Они в 1639-м провели необходимые наблюдения и определили требуемое расстояние от солнца до Земли. Получилось, что астрономическая единица в км. равнялась 95,6 млн. Полученная величина не имела определения, потому что считалась очень приблизительной. Да и труд увидел свет только после кончины ученых в 1661 г.

При измерении параллакса красной планеты Д. Кассини в 1672-м удалось добиться иных результатов. Получив точные результаты орбит Земли и «бога войны» (Марса), ученый решил уточнить труды своего предшественника. После необходимых вычислений значение астрономической единицы составило 140 000 000 км. Но информация не была принята к сведению и постоянно уточнялась.

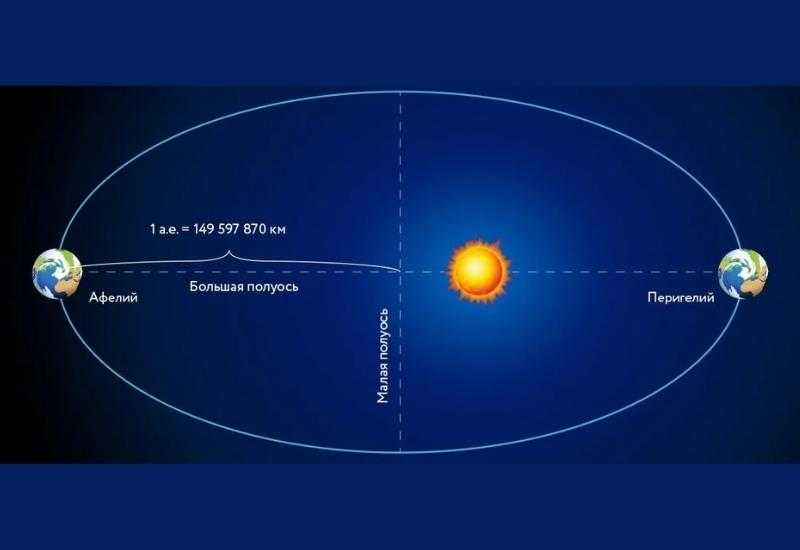
Определение расстояния между Солнцем и Землей

Астрономическими единицами обычно измеряют расстояния до планет внутри солнечной системы. Величина не менее удобна, чтобы высчитать пространство до каких-либо звезд, но в силу объективных причин чаще используется световой год или парсек. Актуальность использования а.е. постепенно снижается. Спустя каждые 7 лет астрономическая единица увеличивается на 1 метр, так что через 100 лет расстояние между солнцем и Землей увеличится на 15 м. Среди различных теорий явления на первый план выходит одна, где парадокс объясняется утратой светилом своей массы за счет воздействия потока ионизированных частиц. 

Что такое фундаментальные астрономические постоянные

Формулы, описывающие движение небесных тел, содержат большое число постоянных величин, которые должны быть определены из наблюдений или экспериментов.

Очевидно, значения этих величин зависят как от совокупности наблюдений, по которым они определены, так и от системы формул, описывающих движение небесных тел. Таким образом, каждая новая теория или даже каждое новое наблюдение, требуют пересмотра всей совокупности постоянных величин.

Но практически такой пересмотр нецелесообразен, хотя и возможен в наше компьютерное время. Чтобы сравнивать между собой наблюдения, сделанные в разное время и из разных мест, планировать полеты космических аппаратов и для многих других целей необходимы значения постоянных, являющиеся общепринятым стандартом.

Такой стандарт в астрономии называют системой фундаментальных постоянных (астрономическими постоянными, хотя многие из них определяются геодезическими, геофизическими и другими методами).

Список астрономических постоянных не регламентирован и меняется в зависимости от потребностей, точности вычислений. Желательно, чтобы числовые значения постоянных, выводимые из большого числа наблюдений, точно удовлетворяли теоретическим соотношениям и разности между принятыми и наблюденными значениями для каждой астрономической постоянной были малыми величинами. Желательно также, чтобы система существовала без изменений в течение длительного времени.

Рекомендации

1. ↑ и
2. В частности, существует барицентрическая небесная система отсчета (BCRS) с центром в барицентре Солнечной системы и геоцентрическая небесная система отсчета (SRCG; на английском языке geocentric celestial reference system , GCRS) с центром в центре масс Земли (включая жидкую среду). конверты). (en) Деннис Д. Маккарти, П. Кеннет Зайдельманн, Время: от вращения Земли к атомной физике , Wiley-VCH ,2009 г., 373  с. , «Резолюция B1.3: Определение барицентрической небесной системы отсчета и геоцентрической небесной системы отсчета. XXIV Генеральная ассамблея Международного астрономического союза (2000 г.). )  » , С.  105
3. Жерар Пети и Брайан Лузум, ред., IERS , техническое примечание IERS № 36: Общие определения и числовые стандарты , Международная служба вращения Земли и систем отсчета ,
   Полный текст документа см. (En) Жерар Пети и Брайан Лузум, редакторы, IERS Conventions (2010): Техническая записка IERS No. 36 , Международная служба вращения Земли и систем отсчета,2010 г.

Таблица используемых астрономических постоянных

Параметр	Символ	Значение	Относительная неопределенность
Определенные константы
Гауссова гравитационная постоянная	k	0,017 202 098 95 A3/2 S−1/2 D−1	точно (по опред.)
Скорость света	c	299 792 458 м/с	точно (по опред.)
Среднее отношение секунды TT к секунде TCG	1 − LG	1 − 6,969 290 134⋅10−10	точно (по опред.)
Среднее отношение секунды TCB к секунде TDB	1 − LB	1 − 1,550 519 767 72⋅10−8	точно (по опред.)
Первичные константы
Среднее отношение секунды TCB к секунде TCG	1 − LC	1 − 1,480 826 867 41⋅10−8	1,4⋅10−9
Световое время на единицу расстояния	τA	499,004 786 3852 s	4,0⋅10−11
Радиус экватора Земли	ae	6,378 1366⋅106 m	1,6⋅10−8
Потенциал геоида	W0	6,263 685 60⋅107 m2 s−2	8,0⋅10−9
Динамический форм-фактор Земли	J2	0,001 082 6359	9,2⋅10−8
Фактор сжатия Земли	1/ƒ	0,003 352 8197 = 1/298.256 42	3,4⋅10−8
Геоцентрическая гравитационная постоянная	GE	3,986 004 391⋅1014 m3 s−2	2,0⋅10−9
Гравитационная постоянная	G	6,673 84⋅10−11 m3 kg−1 s−2	1,2⋅10−4
Отношение массы Луны к массе Земли	μ	0,012 300 0383 = 1/81,300 56	4,0⋅10−8
Наклон эклиптики	ε	23° 26′ 21,406″	*
Производные константы
Постоянная нутации	N	9,205 2331″	*
Астрономическая длина = cτA	A	149 597 870 691 м	4,0⋅10−11
Экваториальный горизонтальный параллакс = arcsin(ae/A)	π☉	8,794 1433″	1,6⋅10−8
Постоянная аберрации для стандартной эпохи 2000	κ	20,495 52″
Гелиоцентрическая гравитационная постоянная = A3k2/D2	GS	1,327 2440⋅1020 m3 s−2	3,8⋅10−10
Отношение массы Солнца к массе Земли = (GS)/(GE)	S/E	332 946,050 895
Отношение массы Солнца к массе (Земли + Луны)	(S/E) (1 + μ)	328 900,561 400
Масса солнца = (GS)/G	S	1,9818⋅1030 кг	1,0⋅10−4
Система планетарных масс: отношение массы Солнца к массе планеты
Меркурий		6 023 600
Венера		408 523,71
Земля + Луна		328 900,561 400
Марс		3 098 708
Юпитер		1047,3486
Сатурн		3497,898
Уран		22 902,98
Нептун		19 412,24
Плутон		135 200 000
Другие константы
Парсек = A/tan(1″)	pc	3,085 677 581 28×1016 м	4,0⋅10−11
Световой год = 365,25 cD	ly	9,460 730 472 5808⋅1015 м	точно (по опред.)
Постоянная Хаббла	H0	70,1 (км/с)/Мпк	0,019
Солнечная светимость	L☉	3,939⋅1026 Вт = 2,107⋅10−15 S D−1	переменная, ±0,1 %

Система астрономических постоянных 1896 года

Саймона Ньюкомб

Первая система фундаментальных астрономических постоянных, обязательная при обработке наблюдений, была принята в 1896 г и 1911 г и действовала вплоть до 1964 г. В основу этой системы были положены результаты исследований Саймона Ньюкомба.

В список астрономических постоянных вошли 14 постоянных величин: постоянные прецессии, нутации, аберрации, параллакс Солнца, экваториальный радиус Земли, ускорение силы тяжести на экваторе и др.

Хотя из-за несогласованности постоянных между собой, отсутствия разделения на основные и выводимые скорее их можно считать списком наиболее точных значений важнейших астрономических постоянных.

Тем не менее первая система постоянных просуществовала почти семьдесят лет.

Еще термины по предмету «Астрономия»

Метеороиды (метеорные тела)

небольшие небесные объекты (гораздо меньше астероидов) в пространстве Солнечной системы, которые движутся вокруг Солнца по эллиптическим орбитам.

Пространство околоземное космическое

область от слоев нейтральной земной атмосферы (точнее, нижних орбит зоны пилотируемой космонавтики ~ 160-200 км) вплоть до лунной орбиты или, по некоторым представлениям — до границы сферы действия Земли (930 тыс. км) общим объемом порядка 1015–1018 км

• Астрономическая единица (а. е.)

• Ея

• Витамин Е

• Изголовь(е)

• Е-волна

• Кормовит Е

• Соевит Е

• Сольвитак Е

• Группа Е

• Весна (астрономически)

• Зима (астрономически)

• Астрономические сумерки

• Астрономический климат

• Астрономические координаты

• Азимут астрономический

• Астрономическая долгота

• Астрономическая зима

• Астрономическая широта

• Астрономический азимут

• Астрономический зенит

Дальнейшее развитие системы фундаментальных астрономических постоянных

В настоящее время в астрономии в общих чертах продолжает использоваться система постоянных 1976 г., утвержденная МАС (с дополнениями от 1994 г. и уточненными в 2009 г. значения). Так как точность изменений и т.п. возрастает с каждым годом, в 2009 году принято решение не изменять существенно саму снову системы астрономических постоянных (как и в 1994 г.), но регулярно обновлять её более свежими данными.

Также, в конце 1980-х г.г. Международная служба вращения Земли (МСВЗ ) выпустила дополняющие систему астрономических постоянных “Стандарты” или “Соглашения” (выходили в 1989, 1992, 1996 г.).

В соглашениях приводятся определения основных систем координат, значения постоянных, которые должны использоваться при обработке наблюдений, описываются методы вычисления различных поправок к координатам станций, указывается, какие эфемериды, модели геопотенциала необходимо использовать.

В 1994 г., примеру МСВЗ последовал и МАС, решивший не менять впредь саму систему (МАС 1976 г), но в то же время при наличии новых данных – выпускать свои варианты “Стандартов” уточняющих основную систему. Аналогичные решения приняты и Международной Ассоциацией Геодезии (МАГ), которая сохранила Геодезическую систему отсчета (Geodetic Reference System) 1980 г как основу для геодезических вычислений.

Численные значения отдельных постоянных могут быть изменены, при этом сама система не меняется. Так как МАГ публикует свой список параметров, общих для астрономии, геодезии и геодинамики (Parameters of Common Relevance of Astronomy, Geodesy, and Geodynamics), то это приводит к путанице, так как постоянные МАГ и постоянные МАС не согласованы друг с другом.

Эмблема Международной службы вращения Земли. Да, есть и такая! Занимается оценкой параметров вращения нашей планеты. Регулярно «укорачивает» и «удлиняет» наши годы на 1-2 секунды!

Внешние ссылки

Системы основного блока
Международная система	Базовые единицы Производные единицы Префиксы Международной системы единиц Новое определение Международной системы единиц на 2018-2019 гг.
Система CGS	сантиметр грамм второй Гауссова система единиц
Астрономическая система	астрономическая единица солнечная масса день
Система натуральных единиц	Система атомных единиц Система геометрических единиц Система единиц Планка Размерный анализ Безразмерная величина Эффект масштаба
Старые измерительные системы	Устаревшие системы Китайские единицы измерения Единицы измерения в Древнем Египте Римские единицы измерения Старые французские единицы измерения Старые испанские единицы измерения Старые мальтийские единицы измерения Традиционные системы Англосаксонские единицы измерения Американские единицы измерения Тайские единицы измерения
Особые системы	Аптекарская система Система условных электрических единиц
Физический размер Физическая постоянная Величина Единица измерения Фундаментальная единица Уменьшенный блок Преобразование единиц Метрология

Как используют астрономическую единицу

Утверждено, что астрономическая единица в световых годах равняется 1,58125e-5. Она относится к перечню внесистемных единиц. Величина успешно используется вкупе с единицами СИ (получила утверждение от сотрудников МБМВ). Ученые РФ могут работать с а. е. без ограничений и учета временных рамок вместе с прочими единицами СИ. С различными приставками (кратными, дольными) применение a.u. исключено.

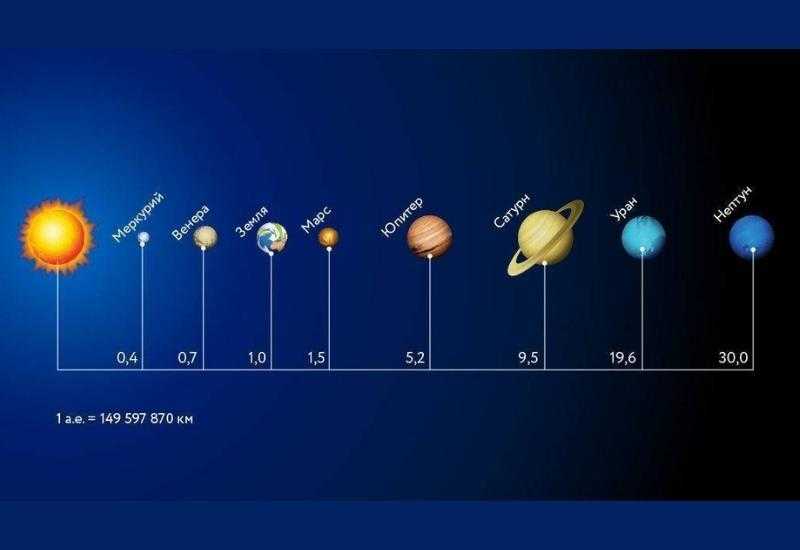
Расстояния в астрономических единицах до планет Солнечной системы

В такой точной науке, как астрономия, исключено понятие астрономическая единица Солнца. С помощью постоянной величины начинающим любителям космоса нетрудно узнать расстояние до внешних, внутренних планет и удаленных объектов: Урана, Нептуна и видимых звезд. С использованием параллакса, угла измерений, когда Земля будет находиться в двух противоположных точках и тригонометрических уравнений, можно получить точный результат.

При измерении а. е. брались данные при прохождении «Вечерней Звезды» по солнечному диску и прочие наблюдения параллаксов (в частности, астероида Эрос, когда орбита далекого гостя пролегала в непосредственной близости в 1901, 1930 гг). Чтобы уточнить информацию, использовался метод радиолокации планет, а в современных условиях положение АМС. В наступившем столетии а.е. равна 149 597 870 700 м.

Астрономическая метафора в медийном дискурсе

В статье рассматривается астрономическая метафора, функционирующая в англоязычном медийном дискурсе. В связи с популяризацией астрономии и изучением космоса происходит активное внедрение в языковое сознание человека астрономических понятий, а, следовательно, астрономической терминологической и нетерминологической лексики, которая часто служит базой метафоризации. Метафорический потенциал астрономической лексики активно используется в медийном дискурсе, цель которого не только информировать аудиторию, но и воздействовать на нее, используя обширные языковые средства, в том числе различные типы метафор. В статье предложено определение астрономической метафоры, итогом семантической классификации выступающих в медийном дискурсе астрономических метафор явилось выделение ряда тематических групп. Процедуры количественного анализа позволили выявить наиболее продуктивные в плане метафоризации тематические группы и отдельные лексические единицы. Проведен функциональный анализ астрономической м…