Измерение дистанции стрельбы коррекцией параллакса, или что такое параллакс?

10 примеров, которые взорвут ваших посетителей!

Если правильно и гармонично использовать эффект параллакса, то можно создать уникальный пользовательский опыт.
Но если сделать плохо, то это отпугнет ваших посетителей или будет отвлекать от основной цели сайта. Будьте особенно
осторожны с мобильной версией, там перебор с параллаксом может настолько замедлить работу браузера,
что посетитель вашего сайта может сильно расстроиться. Рекомендуем тестировать поведение пользователей, чтобы
добиться хороших результатов.

Примеры:

Два крутых американских дизайнера создали сайт, где рассказывают историю своих отношений и
используют при этом параллакс скроллинг. В результате получился романтический рассказ, дополненный классной графикой.

Пример №1

Пример №2

Этот ресторан расскажет вам о своем заведении, меню и поворах с помощью приятных иллюстраций дополненных параллакс эффектом.
Только, пожалуйста, не открывайте этот сайт, если вы голодный.

Пример №3

Хоть тема финансов считается довольно сухой и скучной, этот сайт умудрился сделать из этого увлекательную историю, по просмотру которой вы побежите открывать себе счет.

Пример №4

Пример №5

Epicurrence — это конференция для творческих людей, которая проводится в Америке, штате Колорадо.
Срезу на главном экране нас встречает параллакс эффект с использованием надписи и гор. В меру и со вкусом.

Пример №6

Сюрреалистичные иллюстрации в сочетании с параллаксом дают незабываемый пользовательский опыт, проверьте сами!

Пример №7

Пожалуй, самый яркий промо сайт в этой подборке! На нем вы во всей красе увидите замороженные итальянские морепродукты.

Пример №8

На сайте эпл реализована горизонтальная прокрутка. За счет параллакс эффекта можно покрутить и повертеть Ipad как только вы захотите.
Как всегда минималистичное и стильное решение.

Пример №9

Возможно вы уже встречали ранее этот сайт как пример параллакса. Но нужно признать, сделан он фантастически. Яркая иллюстрация заката
и множество слоев параллакса покоряют с первого раза.

Пример №10

Установка:

Скачиваем и подключаем библиотеку parallax.js или parallax.min.js

Или подключаем используя CDN

<script src=»https://cdnjs.cloudflare.com/ajax/libs/parallax/3.1.0/parallax.min.js»></script>

1	<script src=»https://cdnjs.cloudflare.com/ajax/libs/parallax/3.1.0/parallax.min.js»></script>

Для параллакс контейнера (сцены) задается ID, в котором все прямые дочерние элементы становятся движущимися объектами. Для каждого такого объекта задается атрибут глубины .

Чем больше значение атрибута , тем дальше будет смещаться элемент сцены

<div id=»scene»>
<div data-depth=»0.2″>Дальный слой</div>
<div data-depth=»0.6″>Ближний слой</div>
</div>

1 2 3 4

<div id=»scene»> <div data-depth=»0.2″>Дальный слой</div> <div data-depth=»0.6″>Ближний слой</div> </div>

Также можно задавать отдельные оси смещения и . Подробнее смотрите в

Запускаем параллакс для заданного ID

var scene = document.getElementById(‘scene’);
var parallaxInstance = new Parallax(scene);

1 2	varscene=document.getElementById(‘scene’); varparallaxInstance=newParallax(scene);

В дополнение к оригиналу

Параллакс-эффект сегодня сравним по популярности, пожалуй, со слайдерами-каруселями пять лет назад. Хотя стоит заметить, что последние и до сих пор успешно эксплуатируются.

Если не пускаться в холиварные брюзжания на тему «это тру-параллакс, а это нет», можно вывести такую формулу: и параллакс и не-параллаксовая анимация делают сайт более живым.

Но так как наш блог никогда не ограничивался аргументацией вроде «потому что это красиво», то добавим к вышесказанному несколько тезисов, объясняющих… Зачем параллакс-эффект нужен вашему сайту

На самом деле причины самые простые.

Презентация в действии. Любой моушен всегда куда более презентабелен, чем статичная картинка

Пользователи рефлекторно будут обращать внимание на ваш продукт, если на сайте что-то движется. Возможности для креатива

Параллакс — всего лишь инструмент, но сколько «фишек» можно придумать на его основе! Взять хотя бы вот этот потрясающий по зрелищности пример, который мы недавно публиковали в #SOTD

Возможности для креатива. Параллакс — всего лишь инструмент, но сколько «фишек» можно придумать на его основе! Взять хотя бы вот этот потрясающий по зрелищности пример, который мы недавно публиковали в #SOTD

Ощущение, что кадры снимали камерой, закрепленной на квадрокоптер — но нет, это просто фотошоп и параллакс.

Средство сторителлинга. Маркетологи много говорят о сторителлинге, историях как методе воздействия на целевого посетителя. Концепция «рассказа» как нельзя лучше дополняется навигацией по скроллу и эффектами параллакса в качестве декоративных и дополняющих.

Еще один способ «зацепить» мобильную аудиторию. Параллакс-эффект особенно эффектно смотрится на планшетах и смартфонах с встроенным гироскопом. Наклоняя устройство, пользователь наблюдает смещение объектов в зависимости от степени удаленности — тем самым создается эффект глубины. Элементарно — такой сайт покажут коллегам и проведут на нем больше времени.

Чтобы не выпасть из тренда. Конечно, совсем не обязательно слепо бежать за модой, но в таком случае нужно искать альтернативные пути выделиться. Потому что позиция «я остаюсь на месте, тем и значим» — заведомо проигрышная.

Итак, спасибо Робу за статью и подробные научные доводы. Те, кто читал с планшета, могут напоследок тапнуть по картинке и поиграть с гироскопом

11.2. Годичный параллакс

Угол, под которым с какой-либо звезды виден радиус земной орбиты a, при
условии, что он перпендикулярен направлению на нее, называется
годичным параллаксом звезды (рис. 23).

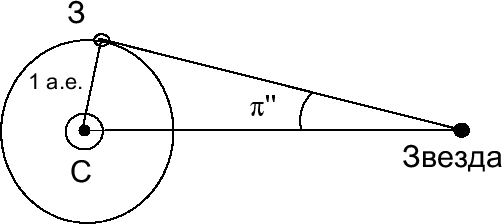Рис. 23. Годичный параллакс

По аналогии с горизонтальным экваториальным параллаксом, зная годичный
параллакс, можно определять расстояния до звезд:

пкпарсекпк18световой годпк

Расстояние до звезды в парсеках определяется через величину годичного
параллакса особенно просто

Задачи

60. (477) Параллакс Солнца p=8″.8, а видимый угловой радиус
Солнца
. Во сколько раз радиус Солнца больше радиуса
Земли?

Решение: Так как параллакс Солнца есть ни что иное, как угловой радиус
Земли, видимый с Солнца, следовательно, радиус Солнца во столько же раз больше
радиуса Земли, во сколько его угловой диаметр больше параллакса

.

61. (482) В момент кульминации наблюденное зенитное расстояние
центра Луны (p=57′) было 50o 00′ 00″. Исправить это наблюдение за
влияние рефракции и параллакса.

Решение: За счет рефракции наблюденное топоцентрическое зенитное
расстояние меньше истинного топоцентрического, т.е.
. Истинное топоцентрическое
зенитное расстояние больше геоцентрического на величину суточного параллакса

.

62.(472) Чему равен горизонтальный параллакс Юпитера, когда он
находится от Земли на расстоянии 6 а.е. Горизонтальный параллакс Солнца
p=8″.8.

63. (474) Наименьшее расстояние Венеры от Земли равно 40 млн. км. В
этот момент ее угловой диаметр равен 32″.4. Определить линейный радиус
этой планеты.

64. (475) Зная, что для Луны p=57’02».7, а ее угловой радиус в
это время
rЛ=15’32».6, вычислить расстояние до Луны и ее линейный
радиус, выраженные в радиусах Земли, а так же площадь поверхности и объем Луны по
сравнению с таковыми для Земли.

65. (483) Наблюденное зенитное расстояние верхнего края Солнца
составляет 64o 55′ 33″, а его видимый радиус
. Найти
геоцентрическое зенитное расстояние центра Солнца, учтя рефракцию и параллакс.

66. Из наблюдений известны годичные параллаксы звезд Вега
()
, Сириус
()
, Денеб
()
. Определить расстояние до этих звезд
в пк и в а.е.

10. Движение планет
| Оглавление |
12. Физические характеристики звезд >>

Публикации с ключевыми словами: задача — общая астрономия — Небесная сфера — системы координат — суточное вращение — рефракция — Сумерки — время — движение планет — расстояние — звезды — галактика Публикации со словами: задача — общая астрономия — Небесная сфера — системы координат — суточное вращение — рефракция — Сумерки — время — движение планет — расстояние — звезды — галактика
См. также: Все публикации на ту же тему >>

Мнение читателя

Астрометрия
—
Астрономические инструменты
—
Астрономическое образование
—
Астрофизика
—
История астрономии
—
Космонавтика, исследование космоса
—
Любительская астрономия
—
Планеты и Солнечная система
—
Солнце

Силы

Проекция Страха: Параллакс обладает огромными силами по «созданию» страха и может с легкостью напугать таких существ, как Супермэн (Superman), Чудо Женщина (WonderWoman), за исключением тех, кто способен понять и преодолеть внутренние страхи, например Кайл Рэйнер и Бэтмэн (Batman).

Контроль разума: Параллакс обладает огромными силами по захвату разума, которых достаточно, чтобы подчинить себе самых сильных существ.

Обладание: Он может завладеть телом существа, если оно испытывает даже малейший страх.

Манипуляции энергией посредством усиления страха: Параллакс, как сущность Страха, может генерировать и управлять огромным количеством энергии. Параллакс способен на все, на что способно Квардианское Кольцо Силы (смотри раздел силы и способности). Также он способен создавать твердые энергетические конструкции. Примером может служить копия Синестро, созданная во время событий Изумрудных Сумерек.

Гипноз

Изменение реальности

Изменение времени

Бессмертие: являясь живым воплощением эмоционального концепта, Параллакс по всем стандартам не может умереть.

Полет

Астрономия | Университетский центр карьеры

 Загрузить PDF

ОТ УЧЕБЫ К НАВЫКАМ

Все академические программы, предлагаемые в UM, помогают учащимся развивать ценные навыки. Астрономия — это область исследований, ориентированная на изучение фундаментальной природы Вселенной, ее происхождения и эволюции, а также физических процессов, происходящих в ней. Будучи студентом-астрономом, вы разовьете широкий спектр навыков — от исследовательских навыков, характерных для астрофизических исследований, до технических и коммуникативных навыков.

Связанные области включают физику, математику, статистику и информатику.

SKILLS AND ABILITIES

Investigative Skills

Defining a research problem Developing a research model Establishing hypotheses Gathering/analyzing data Evaluating ideas Seeing relationships among factors Drawing meaningful conclusions

Communication Skills

Developing and написание исследовательских предложений Обзор литературы по астрономии Суммирование результатов исследований Информирование/объяснение/инструктаж Подготовка технических отчетов

Вычислительные/математические навыки

Измерение расстояний/размеров/отношений Выполняющие расчеты Математическое моделирование . Соответствующие записи . Использование математических форм 9000 3

000

000
000 9000 9000 9000 9000 9000 9000 9000 9000.ships 9011. специализированное оборудование Идентификация и классификация материалов/образцов Наблюдение и интерпретация результатов Запись и анализ данных Разработка и контроль экспериментальных планов Разработка и использование компьютерного моделирования Использование научных инструментов

РАЗВИТИЕ СВОИХ НАВЫКОВ ВНЕ КЛАССА

Работодатели ищут людей, которые могут продемонстрировать отличные устные и письменные навыки общения, работы в команде и межличностного общения навыки, инициативность и трудолюбие.

Студенческие организации и трудоустройство в кампусе предлагают ценные возможности для развития навыков, которые вы развиваете на занятиях. Большинство концентраций спонсируют определенные студенческие группы, такие как студенческая организация или общество чести. Другие варианты включают обучение за границей, работу за пределами кампуса или волонтерство в обществе. Наконец, летняя стажировка может быть лучшим способом проверить свою карьеру и развить рыночные навыки.

ОТ НАВЫКОВ К КАРЬЕРЕ

Навыки, которые вы приобретете в качестве концентратора астрономии, подготовят вас к успеху в ряде областей. Помимо подготовки к исследовательской карьере, астрономы-концентраторы открыли для себя возможности в самых разных профессиях; приведенный ниже список был составлен на основе выпускников UM и национальных данных. Кроме того, концентраторы астрономии могут продолжить свое образование в аспирантуре или профессиональной школе.

Навыки расследования

Исследовательский ученый Специалист по оптическому дизайну Физик частицы Информационный специалист Аналитики управления полетами Атмосферный космос Ученый Биохимик Биофизик

Навыки коммуникации

Пенсионный телевидение 11111111111111111111111111111111111111thENG11111111111111111111111111111111111 ГЛАВНЫЙ ПЕРЕДЕЛА Планировщик музейных выставок Технический писатель Автор веб-страниц Научный журналист Продажи, техническое оборудование

Вычислительные/математические навыки

Компьютерный программист Математический техник Картограф Дизайнер/администратор веб -сайтов .

специалист по оборудованию Художник по спецэффектам

 = Зеленые рабочие места = Требуется дополнительное обучение

для получения дополнительной информации о карьере см. В o*net по адресу http://online.onetcenter.org/

Требования к концентрации

Предварительные условия: Математика 115, 116, 215, 216 . , 340 / 341 Астрономия 160 или другой 100-уровневый обзорный класс

Общие требования: ASTRO 361, 399, 402, 404, 429, плюс факультатив 400-го уровня Математика 450 или 451 9014 Физика 4 390, Один из МАТЕМАТИКА 404, 450, 556 или Физика 451

Департамент астрономии 830 Dennison 734-764-3440 www.astro.lsa.umich.edu

Newnan Advising Center 1255 Angell Hall 1 734-764-0333333333333333333333333333333333333333333333333333333333333н. edu/advising

Чтобы начать общение с профессионалами в интересующих вас областях, создайте собственную учетную запись LinkedIn: www.

Метрология

Необходимо использовать правильную линию визирования, чтобы избежать ошибки параллакса.

Измерения, сделанные путем просмотра положения некоторого маркера относительно объекта измерения, подвержены погрешности параллакса, если маркер находится на некотором расстоянии от объекта измерения и не просматривается с правильного положения. Например, если измерить расстояние между двумя метками на линии с линейкой, нанесенной на ее верхнюю поверхность, толщина линейки отделит ее отметки от меток. Если смотреть из положения, не совсем перпендикулярного линейке, видимое положение сместится, и показания будут менее точными, чем позволяет линейка.

Аналогичная ошибка возникает при считывании положения указателя по шкале в таком приборе, как аналоговый мультиметр . Чтобы помочь пользователю избежать этой проблемы, шкала иногда печатается над узкой полосой зеркала , а глаз пользователя располагается так, чтобы указатель загораживал его собственное отражение, гарантируя, что линия взгляда пользователя перпендикулярна зеркалу и, следовательно, масштаб. Тот же эффект изменяет скорость, считываемую на спидометре автомобиля водителем впереди него и пассажиром сбоку, значениями, считываемыми с не в реальном контакте с дисплеем осциллографа , и т. Д.

Современное состояние вопроса

Макет космического аппарата Gaia на салоне Ле Бурже, 2013

В настоящее время наземные оптические измерения позволяют в некоторых случаях снизить ошибку в измерении параллакса до 0,005″, что соответствует предельному расстоянию в 200 пк. Дальнейшее повышение точности измерений стало возможным благодаря использованию космических телескопов. Специально для астрометрических целей Европейским космическим агентством (ЕКА) в 1989 году был запущен космический телескоп Hipparcos, позволивший измерить параллаксы более 100 тысяч звёзд с точностью до 0,001″. В 2013 году ЕКА запустило новый космический телескоп — Gaia. Планируемая точность измерения параллакса ярких звёзд (до 15 m) будет выше 25 миллионных долей секунды, для слабых звёзд (около 20 m) — до 300 миллионных долей секунды. Измерение годичных параллаксов позволяет производить также один из инструментов Космического телескопа им. Хаббла — Широкоугольная камера 3. Точность измерения параллаксов составляет от 20 до 40 миллионных долей секунды, что позволяет измерять расстояния до 5 килопарсек. В частности, был измерен параллакс переменной звезды SU Возничего.

Значительным достижением конца XX века явилось использование для параллактических измерений метода сверхдальной радиоинтерферометрии. Погрешность при этом может составлять до 10 миллионных долей угловой секунды. Этот метод применяется для измерения расстояния до компактных радиоисточников — космических мазеров, радиопульсаров и др. Так, с помощью этого метода удалось измерить расстояние до объекта Стрелец B2 — газопылевого облака с бурным звездообразованием, находящимся в 100-120 парсеках от центра нашей Галактики. Результаты измерений показали, что Стрелец B2 расположен на расстоянии 7,8±0,8 кпк, что даёт расстояние до центра Галактики 7,9±0,8 кпк. Измерение параллаксов ультракомпактных внегалактических радиоисточников является одной из целей планируемого российского космического эксперимента Миллиметрон — космической обсерватории миллиметрового, субмиллиметрового и инфракрасного диапазонов.

История

Суточным (геоцентрическим) параллаксом называется угол, под которым виден земной радиус с определенного небесного тела. Кроме того, выделяют понятие горизонтального параллакса. Горизонтальным параллаксом называется угол, под которым виден экваториальный радиус Земли из центра определенного небесного тела при нахождении последнего на истинном горизонте (истинный горизонт — мысленно воображаемый большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии в точке наблюдения). Различия понятий суточного и горизонтального параллакса связаны с несферичностью Земли (так полярный радиус Земли короче экваториального радиуса на 21 км).

Суточный параллакс сыграл очень важную роль в истории астрономии, как наиболее простой и достоверный способ определения расстояния до объектов Солнечной Системы. Фактически этот метод являлся единственным геометрическим методом измерения расстояний в Солнечной Системе вплоть до радиолокации, лазерной локации и методов радиоинтерференции сигналов межпланетных станций. Базой суточного параллакса является земной радиус. Самым большим суточный параллакс является у Луны (57 угловых минут) и у Солнца (9 угловых минут). У всех планет Солнечной Системы суточный параллакс подвержен регулярным изменениям и значительно меньше угловой минуты (у Венеры  0.1-0.6 угловых минут, у Марса 0.1-0.4 угловых минут, у Юпитера и Сатурна меньше 0.1 угловой минуты, а у Урана и Нептуна меньше одной угловой секунды).

Первыми параллакс Луны и Солнца определили древнегреческие астрономы на основе наблюдений лунных затмений, которые позволяли определять параллакс Луны из одного и того же места. Так древнегреческий астроном Гиппарх Никейский (180-125 годы до нашей эры) в 129 году до нашей эры оценил параллакс Солнца в 7 угловых минут (максимальная величина угла, который неразличим невооруженным глазом). Похожие расчеты выполнил до него другой древнегреческий астроном Аристарх Самосский (310-230 годы до нашей эры).

С другой стороны, александрийский астроном Клавдий Птолемей (100-170 годы нашей эры) полагал, что расстояние до Луны зависит от её фаз. Это говорит о больших разногласиях среди астрономов Древнего мира по поводу оценок параллаксов Луны и Солнца. Позже ошибка Птолемея о зависимости размера параллакса Луны от её фаз стала одним из основных объектом критики птолемевской системы мира. Так юный Николай Коперник (1473-1543 годы нашей эры) во время учебы в Италии проводил измерения параллакса Луны вместе со своим учителем Новарой. Наблюдения положения Луны во время затмения яркой звезды Альдебаран из Болоньи 9 марта 1497 года показали, что параллакс Луны не зависит от её фазы. В последующие века началось широкое использование одновременных наблюдений из северного и южного полушария для точного измерения параллаксов Луны, Солнца и Марса. К примеру, в 18 веке такие наблюдения осуществлялись в обсерватории мыса Доброй Надежды в южной части Африки и Берлинской обсерватории.

Частные случаи использования суточного и годичного параллакса

Многие тысячи лет число известных объектов в Солнечной Системе было постоянным и было равно девяти (Земля, Луна, Солнце, Меркурий, Венера, Земля, Марс, Юпитер и Сатурн). Это постоянство нарушали лишь кометы, которые периодически появлялись во внутренних областях Солнечной Системы. В 18 веке в Солнечной Системе начались открытия новых планет и астероидов (к примеру, Урана и Цереры). Шквал новых открытий вынудил астрономов разрабатывать методики по вычислению орбит небесных тел Солнечной Системы по минимальному числу измерений. В 1801 году 24-летний немецкий математик Фридрих Гаусс (1777-1855 годы) с целью обнаружения потерянной Цереры разработал математический метод, по которому было возможно определить орбиту небесного тела на основе всего трех его наблюдений.

В то же время примерное расстояние до небесного тела в Солнечной Системе, возможно, определить лишь по двум наблюдениям. Особенно, это актуально в случае открываемых объектов за орбитой Нептуна (ТНО). У таких объектов скорость движения является минимальной по сравнению с орбитальной скоростью Земли (несколько сотен метров в секунду против 30 км в секунду). В результате этого наблюдаемое расстояние от Солнца (гелиоцентрическое расстояние) до ТНО в астрономических единицах можно определить простым соотношением 150/q, где q – это угловая скорость объекта в угловых секундах за один час.

С другой стороны в последние годы астрометрические наблюдения мигрируют из оптического диапазона в более длинноволновые диапазоны электромагнитного спектра: инфракрасные лучи и радиоволны. Первый диапазон является очень перспективным для астрометрии красных и коричневых карликов во Вселенной (наиболее распространенной популяции массивных объектов в галактике, чей максимум теплового излучения приходится на инфракрасный диапазон). Второй диапазон является уникальным во всем электромагнитном спектре по проникающей способности.

Так недавно радиоастрономы с помощью радиоинтерферометра VLBA смогли установить рекорд самого далекого измеренного параллакса: расстояние до межзвездного облака G007.47+00.05 (внешний рукав Щита – Центавра) составило 20 тысяч парсек или 67 тысяч световых лет

Как измеряется расстояние до звезд и что такое световой год?

Расстояния между звездами настолько велики, что измерять их километрами или милями – занятие с бесконечными нолями. Привычную систему измерений применяют для обозначения расстояний в одной системе. К примеру называют, что минимальное расстояние от Земли до Марса – 55,76 миллионов километров. Со звездами всё сложнее, и здесь обычно используют понятия светового года и парсека.

Астрономическая единица – принятая в астрономии единица измерения объектов Солнечной системы и ближайших к ней объектов Вселенной. Астрономическая единица равна 149 598 100 км (+- ~750 км), что приблизительно равняется среднему расстоянию Земли от Солнца. Современные наблюдения зафиксировали постепенно увеличение значения на 15 см ежегодно, что объясняется, возможной потерей Солнцем массы, последствия солнечного ветра.

Световой год – расстояние, которое свет проходит за один год, в метрах это 9 460 730 472 580 800. На самом деле свет звезд, который мы видим в безоблачную ночь, шёл до нашей планеты многие столетия, а некоторые из них вообще больше не существуют.

Парсек, он же «параллакс угловой секунды» – это расстояние, с которого средний радиус орбиты Земли (перпендикулярный лучу зрения), виден под углом в одну секунду угловую. Если совсем просто, то парсек = 3,26 световым годам.

Интересно то, что в научно-популярной и фантастической литературе принято использовать понятие светового года, а парсеками обычно пользуются только в профессиональных трудах и исследованиях.

Ближайшая к нам звезда – это Альфа Центавра, которая находится от Земли на расстоянии в 4,37 световых лет. А вот до самой удалённой галактики (по состоянию на декабрь 2012 года) от Земли целых 13,3 миллиардов световых лет!. Получается, когда солнце этой самой галактики (известной под индексом UDFj-39546284) потухнет, человечество об этом узнает еще не скоро.

Расстояния в цифрах

• Меркурий– ближайшая к Солнцу планета, среднее расстояние от Солнца 0,387 а. е (58 млн. км), а расстояние до Земли колеблется от 82 до 217 млн. км. Меркурий движется вокруг Солнца по сильно вытянутой эллиптической орбите, плоскость которой наклонена к плоскости эклиптики под углом 7°.
• Венера– вторая по удаленности от Солнца планета, среднее расстояние от Солнца 0,72 а.е. (108,2 млн. км). Средний радиус планеты составляет 6051 км, масса – 4,9 на 10 в 24 степени кг (0,82 массы Земли), средняя плотность 5,24 г/см3.
• Земля– третья от Солнца планета Солнечной системы, среднее расстояние от Солнца 1 а.е. (149,6 млн. км), средний радиус 6371,160 км (экваториальный 6378, 160 км, полярный 6356,777 км), масса – 6 на 10 в 24 степени кг.
• Марс– четвертая планета от Солнца, среднее расстояние от Солнца составляет 1,5 а.е. (227,9 млн. км). Минимальное расстояние от Марса до Земли составляет 55,75 млн. км, максимальное – около 401 млн. км.
• Юпитер– пятая по счету от Солнца, а также крупнейшая планета Солнечной системы, среднее расстояние от Солнца 5,2 а.е.(778 млн. км), экваториальный радиус равен 71,4 тыс. км, полярный – около 67 тысяч км, масса 1,9 на 10 в 27 степени кг (317,8 массы Земли), средняя скорость обращения вокруг Солнца – 13,06 км/с.
• Сатурн– шестая планета от Солнца и вторая по размерам планета в Солнечной системе после Юпитера. Среднее расстояние Сатурна от Солнца 9,54 а.е. (1,427 млрд. км), средний экваториальный радиус около 60,3 тысяч км, полярный – около 54 тысяч км, масса 5,68 на 10 в 26 степени кг (95,1 массы Земли).
• Уран– седьмая от Солнца планета Солнечной системы. Планета была открыта в 1781 году английским астрономом Уильямом Гершелем и названа в честь греческого бога неба Урана. Среднее расстояние от Солнца 19,18 а.е. (2871 млн. км), средний радиус 25560 км, масса 8,69 на 10 в 25 степени (14,54 массы Земли), средняя плотность – 1,27 г/см3.
• Нептун– восьмая планета от Солнца и четвертая по размеру среди планет. Нептун открыт в Берлинской обсерватории 23 сентября 1846 года немецким астрономом Иоганном Галле на основании предсказаний, сделанных независимо математиком Джоном Адамсом в Англии и астрономом Урбеном Леверрье во Франции. Среднее расстояние планеты Нептун от Солнца 30,1 а.е. (4497 млн. км), средний радиус около 25 тысяч км, масса 1,02 на 10 в 26 степени кг (17,2 массы Земли), плотность 1,64 г/см3.
• Плутоном– в честь древнеримского бога подземного царства. В тот момент предполагали, что его масса сравнима с массой Земли, но позже было установлено, что масса Плутона почти в 500 раз меньше земной, даже меньше массы Луны. Масса Плутона 1,2 на 10 в22 степени кг (0,22 массы Земли). Среднее расстояние Плутона от Солнца 39,44 а.е. (5,9 на 10 в12 степени км), радиус около 1,65 тысяч км.

Фотография

Дальномер Contax III с настройкой макросъемки . Поскольку видоискатель находится на верхней части объектива и в непосредственной близости от объекта, перед дальномером устанавливаются очки, а для компенсации параллакса устанавливается специальный видоискатель.

Неудачное панорамное изображение из-за параллакса, так как ось вращения штатива не совпадает с точкой фокусировки.

Ошибка параллакса может быть замечена при съемке фотографий с помощью многих типов камер, таких как зеркальные камеры с двумя объективами и камеры с видоискателями (например, дальномерные камеры ). В таких камерах глаз видит объект через другую оптику (видоискатель или второй объектив), чем та, через которую делается фотография. Поскольку видоискатель часто находится над объективом камеры, фотографии с ошибкой параллакса часто немного ниже, чем предполагалось, классическим примером является изображение человека с обрезанной головой. Эта проблема решается в однообъективных зеркальных камерах , в которых видоискатель видит через тот же объектив, через который делается фотография (с помощью подвижного зеркала), что позволяет избежать ошибки параллакса.

Параллакс также является проблемой при сшивании изображений , например, для панорам.

Светимость

Светимость  — название ряда физических величин .

В фотометрии светимость  — это световая величина , представляющая собой световой поток излучения, испускаемого с малого участка светящейся поверхности единичной площади . Она равна отношению светового потока, исходящего от рассматриваемого малого участка поверхности, к площади этого участка:

где dΦv — световой поток, испускаемый участком поверхности площадью d S . Светимость в Международной системе единиц (СИ) измеряется в лм /м². 1 лм/м² — это светимость поверхности площадью 1 м2, излучающей световой поток, равный 1 лм.

Аналогом светимости в системе энергетических фотометрических величин является энергетическая светимость (излучательность). Её определение аналогично определению светимости, но вместо светового потока Φvиспользуется поток излучения Фe. Единица энергетической светимости в СИ — Вт /м².

Светимость в астрономии  — полная энергия , излучаемая астрономическим объектом ( планетой , звездой , галактикой и т. п.) в единицу времени . Измеряется в абсолютных единицах ( СИ  — Вт ; СГС  — эрг /с) либо в единицах светимости Солнца ( L ☉ = 3,86⋅1033 эрг /с = 3,86⋅1026Вт).

Светимость астрономического объекта не зависит от расстояния до объекта, от него зависит только видимая звёздная величина . Светимость — одна из важнейших звёздных характеристик, позволяющая сравнивать между собой различные типы звёзд на диаграммах «спектр — светимость» , «масса — светимость». Светимость звезд главной последовательности можно приближенно рассчитать по формуле:

Светимость самых ярких звёзд в миллионы раз превышает светимость Солнца.

В экспериментальной физике элементарных частиц светимостью называют параметр ускорителя , характеризующий интенсивность столкновения частиц пучка с частицами фиксированной мишени (интенсивность столкновения частиц двух встречных пучков в случае коллайдеров ). Светимость L измеряется в см−2·с−1. При умножении сечения реакции на светимость получается средняя частота протекания этого процесса на данном коллайдере N˙process=L⋅σprocess{\displaystyle {\dot {N}}_{\text{process}}=L\cdot \sigma _{\text{process}}} .

Светимость Большого адронного коллайдера во время первых недель работы пробега была не более 1029частиц/см²·с, но она продолжает постоянно повышаться. Целью является достижение номинальной светимости в 1,7⋅1034частиц/см²·с, что по порядку величины соответствует светимостям BaBar ( SLAC , США) и Belle ( KEK , Япония ). Коллайдеру KEKB принадлежит мировой рекорд светимости для ускорителей с встречными пучками — 2,11⋅1034см−2·с−1.