Физика 9 класс

Графики равномерного прямолинейного движения

Построение графика

Очень важно уметь описывать движение графиком. Это может значительно упростить решение задачи

Давай посмотрим, как с помощью графика описать равномерное прямолинейное движение.

Любой график – множество точек, который показывает зависимость одного значения от другого. Эта зависимость определяется каким-то уравнением.

Например, когда мы строим параболу, мы руководствуемся уравнением \(y={{x}^{2}}\). Как еще это можно записать?

Вот так: \(f(x)={{x}^{2}}\). Это показывает, что функция \(f\) зависит от значения \(x\).

Давай аналогично составим график движения тела. Вспомним то главное уравнение:

Иными словами, это график зависимости координаты тела от времени. Давай так и запишем:

Начинаем работать с уравнением. Предположим, что нам известна проекция скорости и начальное положение тела. Работать с конкретными числами удобнее.

Пусть: \({{V}_{x}}=0.5\)м/с и \({{x}_{0}}=3\)м

Тогда уравнение имеет вид: \(x=3+0.5\cdot t\)

Нарисуем оси и обозначим их. Так как у нас даны единицы измерения (метры и секунды), мы обязательно должны подписать их рядом с названиями осей!

Теперь можем взять и рассмотреть положение тела в любую секунду: хоть в первую, хоть в двенадцатую!

Отметим точки и соединим их. Получим график движения.

А теперь вопрос на засыпку: может ли время быть отрицательным?

Могу ли я указать положение тела в минус третью секунду? Могу.

Для этого стоит помнить, что «нулевая» секунда – момент, когда мы запускаем секундомер, когда мы только начинаем наблюдать за телом. Но оно могло двигаться и до того, как мы включили таймер, верно?

Давай покажем движение тела до наших наблюдений пунктирной линией:

Зачастую точки пересечения графика с осями несут в себе очень важную информацию!

Например, когда мы только включили секундомер (\(t=0\)с), тело находилось в начальном положении (\({{x}_{0}}=3\)м), и это видно по графику!

А когда координата тела была равна нулю?

Все очень просто: за 6 секунд до того, как мы включили секундомер! Прямая пересекает ось времени в точке -6.

Итак, мы выяснили, что…

И действительно, само уравнение \(x={{x}_{0}}+{{V}_{x}}\cdot t\) уже напоминает стандартное уравнение прямой, которое мы изучаем на математике: \(y=kx+m\), где \(m\) — точка пресечения графика с осью Х, а \(k\) — коэффициент наклона прямой.

Относительность движения. Операции над скоростями

Давай вспомним одну из важнейших вещей, когда мы говорим про движение. Мы давали ему определение, когда говорили о кинематике в целом.

Это тело отсчета. То тело, относительно которого мы рассматриваем движение.

Мы уже знаем, что относительно одного тела тело может нестись с бешеной скоростью, а относительно другого не двигаться вовсе.

От системы отсчета зависит изменение положения тела. А что еще от нее зависит? Траектория зависит?

Оказывается, да!

Однажды человек изобрел колесо и изменил мир. Давай воспользуемся этим изобретением для того, чтобы найти ответ на вопрос выше.

Возьмем какую-то точку на колесе и пусть оно катится по дороге! Как движется эта точка относительно оси колеса? По кругу.

А относительно Земли?

Вот так:

Круто, да?

Эта кривая называется циклоида. И она точно отличается от траектории движения точки относительно оси колеса.

Сегодня мы научимся определять и связывать скорости в разных системах отсчета.

А еще на относительности основан главный закон скоростей – закон об их сложении.

Поступим как настоящие ученые. Готовые формулы – для слабаков. Мы будем выводить их сами.

Рассмотрим ситуацию.

По реке плывет плот (П) со спортсменом (С). На берегу реки сидит рыбак (Р) и наблюдает за этим. В какой-то момент пловец прыгает с плота и движется к другому берегу реки. Их несёт течение реки.

Давай изобразим это:

Давай нарисуем вектор перемещения спортсмена относительно плота и назовем его относительным перемещением:

Теперь нарисуем вектор перемещения плота, которого несет течение. Назовем этот вектор переносным:

А теперь посмотрим, как спортсмен двигался относительно рыбака, и назовем вектор этого перемещения абсолютным:

Ты только посмотри! У нас тут треугольник!

Нет, оставь свои теории заговора и иллюминатов. Не тот треугольник. Треугольник суммы векторов!

Переносное перемещение и относительное в сумме дают абсолютное!

Как связать перемещение со скоростью? Нужно поделить его на время!

Та-а-ак… А его откуда брать?

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?

1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с

2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?

1) 0,25 м
2) 6 м
3) 10 м
4) 150 м

3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — ​\( v_1 \)​ и скорости «Пежо» — \( v_2 \).

1) ​\( v_1=v_2 \)​
2) ​\( v_1=2v_2 \)​
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)

4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости ​\( v_1 \)​ и \( v_2 \).

1) ​\( v_1=v_2 \)​
2) ​\( v_1=2v_2 \)​
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)

5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен

1) 20 м
2) 40 м
3) 80 м
4) 160 м

6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен

1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с

7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости ​\( v_1 \)​, \( v_2 \) и \( v_3 \) движения этих тел.

1) ​\( v_1=v_2=v_3 \)​
2) \( v_1>v_2>v_3 \)​
3) \( v_1<v_2<v_3 \)​
4) ​\( v_1=v_2 \), \( v_3<v_1 \)

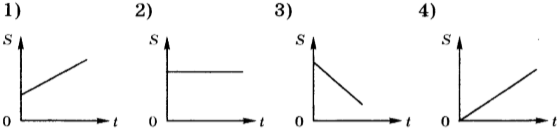
8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?

9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?

1) 9,8 м
2) 6 м
3) 4 м
4) 2 м

10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид

1) ​\( x=1t \)​ (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)

11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость

ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит

12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.

1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось

Часть 2

13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?

Таблица сравнения равномерного и неравномерного прямолинейного движения

Характеристика	Равномерное прямолинейное движение	Неравномерное прямолинейное движение
Определение	Движение, при котором тело перемещается по прямой линии с постоянной скоростью.	Движение, при котором тело перемещается по прямой линии с переменной скоростью.
Скорость	Постоянная скорость на протяжении всего движения.	Скорость меняется в течение движения.
Ускорение	Отсутствует (ускорение равно нулю).	Может быть как положительным, так и отрицательным.
График зависимости скорости от времени	Горизонтальная прямая линия.	Линия с наклоном, может быть прямой или кривой.
Примеры	Автомобиль, движущийся по прямой дороге с постоянной скоростью.	Тело, падающее под действием силы тяжести.

Решение задач на среднюю скорость и действия со скоростями

Задача 8 (продолжение задачи 3  ). Поймавший Петю директор пишет замечание в его дневник, его ручка движется по листу бумаги со скоростью 0.05 м/с. Через 3 секунды Петя взмолится перед Максимом Михайловичем, его ручка станет двигаться со скоростью 0.03 м/с на протяжении 4 секунд.

А если бедному ученику повезёт и ручка начнет плохо писать, то, чтобы расписать ее, директор будет давить на нее сильнее в течение 5 секунд и скорость ее станет равна 0.01 м/с.

Найдите среднюю путевую скорость ручки. Зная, что длина красноречивого замечания равна 24 см, найдите среднюю скорость ручки по перемещению.

Механическое движение. Система отсчёта. Закон относительности движения

Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.

То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).

Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.

Рисунок 1 – Иллюстрация к примеру

Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение

Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета

То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение

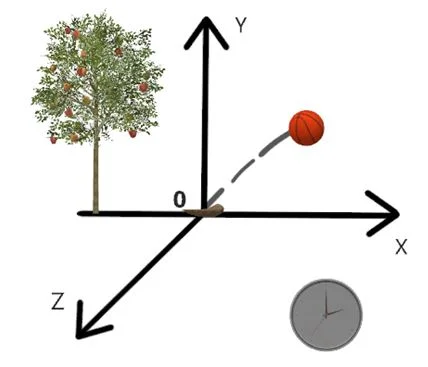Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)

Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.

Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку. Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь

Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.

Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как  материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см

рисунок 8). Радиус-вектор, проведенный в точку A обозначим r, а радиус-вектор в точку Б обозначим r1. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

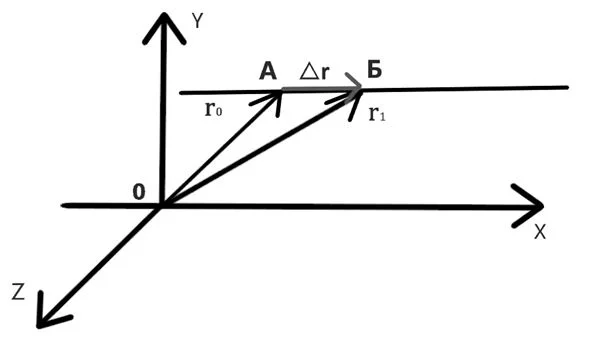
Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r₁ — r. Тогда выражение для скорости можно переписать в виде:

Из этого выражения следует:

r₁ = r + v*t.

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

r= r + v*t.

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

r_x = r_0x + v_x*t;

r_y = r_0y + v_y*t;

r_z = r_0z + v_z*t.

В этих выражениях r_0x, r_0y, r_0z и v_x, v_y, v_z– это компоненты изначальных векторов r и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

r_x = r_0x + v_x*t;
r_y = r_0y + v_y*t;
r_z = r_0z + v_z*t.

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х) и конечной (х₁) точки на ось ОХ.

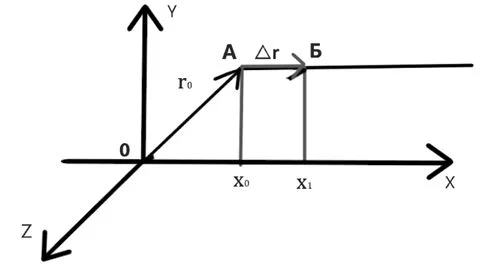Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

x(t) = x+ v*t.

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

S(t) = S + v*t.

Если точка начала двигаться из начала отсчета S = 0, можно переписать эту формулу в виде:

S(t) = v*t.

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

x = 3 см = 0,03 м.

Теперь можно записывать уравнение для координаты х:

x(t) = x+ v*t = 0,03 + 5*t.

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2)  = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:

x(t) = x- v*t = 0,03 — 5*t.

График зависимости проекции вектора скорости от времени

И все-таки, чаще мы будем иметь дело с задачами, при решении которых нам понадобится использовать проекции векторов.

Например, обратимся к задаче с катерами из прошлого урока. Два катера двигаются в противоположных направлениях (рисунок 6). Один из них проходит $60 \space км$, а другой — $50 \space км$. Пусть эти перемещения совершены за время $t_1$, равное $2 \space ч$.

Рисунок 6. Иллюстрация к задаче

В этом случае векторы скорости и перемещения первого катера будут сонаправлены друг другу, как и векторы скорости и перемещения второго катера. Их проекции: для первого катера они будут положительными, а для второго — отрицательными.

Проекция скорости первого катера:$s_{1x} = \upsilon_{1x} t_1$,$\upsilon_{1x} = \frac{s_{1x}}{t_1}$,$\upsilon_{1x} = \frac{60 \space км}{2 \space ч} = 30 \frac{км}{ч}$.

Проекция скорости второго катера:$\upsilon_{2x} = \frac{s_{2x}}{t_1}$,$\upsilon_{2x} = \frac{−50 \space км}{2 \space ч} = −25 \frac{км}{ч}$.

А теперь взгляните на графики зависимости проекций векторов скорости от времени (рисунок 7).

Рисунок 7. Графики зависимости проекций векторов скорости от времени движения

Какую информацию о движении двух тел можно получить по графикам, изображенным на рисунке 7?

Здесь мы видим и числовые значения проекций векторов скорости, и их знаки, а также знаки проекций перемещений, которые совершили катера за время $t_1$. Проекции этих перемещений численно равны площадям под графиками:

• проекция вектора перемещения $s_{1x}$ больше нуля и численно равна площади оранжевого прямоугольника;
• проекция вектора перемещения $s_{2x}$ меньше нуля и численно равна площади голубого прямоугольника.

{"questions":,"answer":}}}]}

Равномерное прямолинейное движение в физике — формулы и определения с примерами

Равномерное прямолинейное движение:

Вы изучали равномерное прямолинейное движение, познакомились с понятием «скорость». Скалярной или векторной величиной является скорость? Каковы закономерности равномерного прямолинейного движения?

Вы знаете, что движение, при котором за любые равные промежутки времени тело проходит одинаковые пути, называется равномерным. В каком случае одинаковыми будут не только пути, но и перемещения?

Проделаем опыт. Проследим за падением металлического шарика в вертикальной трубке, заполненной вязкой жидкостью (например, густым сахарным сиропом) (рис. 43). Будем отмечать положение шарика через равные промежутки времени. Опыт показывает, что за равные промежутки времени, например за

Сделаем вывод. При равномерном прямолинейном движении тело за любые равные промежутки времени совершает одинаковые перемещения и проходит одинаковые пути.

В 7-м классе вы находили скорость равномерного движения тела как отношение пути к промежутку времени, за который путь пройден: Это отношение показывает, как быстро движется тело, но ничего не говорит о направлении движения. Чтобы скорость характеризовала и быстроту движения, и его направление, ее определяют через перемещение.

Скорость равномерного прямолинейного движения — это величина, равная отношению перемещения к промежутку времени, за который оно совершено:

Из равенства (1) следует, что скорость — векторная физическая величина. Ее модуль численно равен модулю перемещения за единицу времени, а направление совпадает с направлением перемещения (т. к. ).

Отношение для всех участков движения на рисунке 43 одинаково: Значит, скорость равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.

Из формулы (1) легко найти перемещение:

и путь (равный модулю перемещения ):

А как определить положение равномерно и прямолинейно движущегося тела в любой момент времени Рассмотрим пример. Автомобиль движется с постоянной скоростью по прямолинейному участку шоссе (рис. 44).

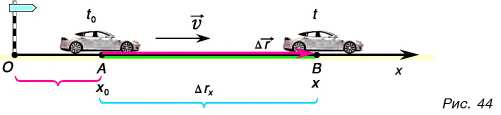
Автомобиль рассматриваем как материальную точку. Из формулы (2) находим проекцию перемещения автомобиля на ось Ох:

Согласно рисунку 44 за время автомобиль совершил перемещение Подставляя в равенство (4), получим:

Приняв запишем формулу для координаты автомобиля:

Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.

Зависимость координаты движущегося тела от времени называется кинематическим законом движения. Формула (5) выражает кинематический закон равномерного прямолинейного движения.

Для измерения скорости используются специальные приборы. В автомобилях имеется спидометр (рис. 45), на самолетах — указатель скорости. Эхолокаторы измеряют скорость тел, движущихся под водой, а радиолокаторы (радары) — в воздухе и по земле. Сотрудники службы дорожного движения с помощью портативного радара с видеокамерой (рис. 46) регистрируют скорость транспортных средств.

Для любознательных:

Скорости движения могут сильно отличаться. За одну секунду черепаха может преодолеть несколько сантиметров, человек — до 10 м, гепард — до 30 м, гоночный автомобиль — около 100 м.

Около 8 км за секунду пролетает по орбите спутник Земли (рис. 47). Но даже скорости космических кораблей «черепашьи» по сравнению со скоростью микрочастиц в ускорителях. В современном ускорителе (рис. 48) электрон за одну секунду пролетает почти 300 000 км!

Главные выводы:

1. При равномерном прямолинейном движении за любые равные промежутки времени тело совершает одинаковые перемещения.
2. Скорость равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.
3. При равномерном прямолинейном движении тела модуль перемещения равен пути, пройденному за тот же промежуток времени.
4. Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.

Пример решения задачи:

Кинематический закон прямолинейного движения лодки но озеру вдоль оси Ох задан уравнением где

Определите: 1) проекцию скорости лодки 2) координату лодки в момент времени 3) проекцию перемещения лодки на ось Ох и путь, пройденный лодкой за время от момента до момента

Решение

Сделаем рисунок к задаче.

По условию задачи координата лодки линейно зависит от времени. Значит, лодка движется равномерно. Сравнив получим

Найдем

Из рисунка 49: проекция перемещения

Ответ:

Примеры решения задач

Однако не при любом виде движения можно использовать данную формулу для определения перемещения. Существует ряд особенностей (рассмотрены ниже, в виде примеров), в которых действия имеют иной характер.

Задача 1

Каков модуль и каково направление скорости тела, если известно, что движение равномерно и происходит вдоль оси OX. С начала движения прошло 4 секунды, а координата изменилась с 5м до -3м.

Решение

Выше было рассмотрено, что отражением модуля и направления вектора являются проекции на оси координат. Поскольку движение характеризуется равномерностью, то проекцию скорости на ось абсцисс можно определить по следующей формуле:

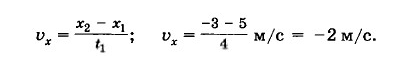
Проекция может иметь отрицательный знак. В таком случае скорость точки иметь направление, противоположное положительному по оси OX. Модуль скорости \(V=|Vx|=|-2м/с|=2м/с.\)

Задача 2

Расстояние между пунктами A и B по прямой линии 20 км. Навстречу друг другу из этих пунктов одновременно выехали два автомобиля. Первый имел скорость 50 км/ч, второй — 60 км/ч.

Необходимо определить места положения автомобилей относительно пункта А через полчаса с момента начала движения, а также на каком расстоянии они будут друг от друга в этот момент.

Решение.

Автомобили совершают движения, которые можно выразить формулами:

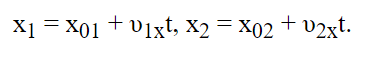
Спустя полчаса (0,5ч), их положение математически можно выразить так:

Один из автомобилей достигнет точки C, отдаленной от старта движения на 25 км вправо от A. Второй автомобиль достигнет точки D, которая отдалена влево на 10 км. Таким образом, модуль расстояния составит разность их координат:

\(S=|X2-X1| =|-10км-25км|=35км\)

Соответственно пройденные расстояния можно найти по формулам:

\(S1=V1t=50 км/ч*0,5ч=25км\)

\(S2=V2t=60 км/ч*0,5ч=30км\)

Задача 3

Автомобиль выехал из пункта A в пункт B со скоростью V1. Через время t0 пункт B покинул второй автомобиль и направился в том же направлении. Его скорость составила V2. Расстояние между пунктами обозначаем S. Где будет находиться место встречи автомобилей (выразить через пункт B)? Какое время пройдет до их встречи (выразить через первый автомобиль)?

Решение

Задача № 3

Автомобиль выехал из пункта A в пункт B со скоростью V₁. Через время t пункт B покинул второй автомобиль и направился в том же направлении. Его скорость составила V₂.

Расстояние между пунктами обозначаем S.

Где будет находиться место встречи автомобилей (выразить через пункт B)? Какое время пройдет до их встречи (выразить через первый автомобиль)?

Решение

При встрече автомобилей их координаты будут равны: X₁=X₂=X_в

В целом уравнения движения в данном случае выглядят так:

X₁=V₁t

X₂=S+V₂(t-t)

Производя математические действия, получаем:

V₁t_в=S+V₂(t_в-t)

Вероятно, V₁>V₂, S>V₂t

Место встречи автомобилей можно найти по формуле: