Математическая модель: что это и как ее создать

Что такое математическая модель

Математическая модель также была создана для того, чтобы проанализировать и предугадать поведение материального объекта. Однако у математической модели есть проблема, от которой не избавиться — идеализация.

Все науки, которые используют для решения своих задач математический аппарат, практикуют математическое моделирование. То есть, заменяют объект своего исследования математической моделью и занимаются исследованием последней.

При помощи совокупности математических методов можно описать образцовый объект или процесс, который построен на стадии содержательного моделирования.

Как осуществляется связь математической модели и реальности?

Эмпирические законы.
Гипотезы.
Идеализация.
Упрощения.

Однако стоит помнить, что модель — объект, она может иметь собственные качества и свойства, которые могут не относиться к реальному моделируемому объекту.

Часто математические модели представляют в виде:

Графика. Получить данные для решения задачи мы можем, посмотрев на данные графика.
Уравнения. Данные для решения задачи зашифрованы в виде уравнения, под буквами x и y.

Гносеология

Гносеология или эпистемология — это отрасль философии, изучающая природу знания и его возможности, связь знания с реальностью и раскрывающая условия достоверности и правдивости знания. Термин «гносеология» происходит от греческих слов «гнозис» — знание и «логос» — понятие, учение и означает «понятие знания», «учение о знании». Эта доктрина исследует природу человеческих знаний, формы и закономерности перехода от поверхностного взгляда на вещи (мнения) к постижению их сущности (истинного знания), и поэтому рассматривает вопрос о путях истины, ее критериях. Наиболее животрепещущим вопросом для всей гносеологии является вопрос о том, в чем практический смысл достоверных знаний о мире, о самом человеке и о человеческом обществе. И хотя термин «эпистемология» был введен в философию относительно недавно (1854 г.) шотландским философом Й. Феррером, доктрина знания была разработана еще со времен Гераклита, Платона и Аристотеля.

Эпистемология рассматривает универсальную в познавательной деятельности человека, независимо от того, что это за деятельность: мирская или специализированная, профессиональная, научная или художественная. Поэтому эпистемологию (теорию научного знания) можно назвать подразделением гносеологии, хотя в литературе эти две науки часто отождествляются, что не соответствует действительности.

Определим предмет и объект знания, без которого процесс познания невозможен.

Предмет знания — это тот, кто его осознает, то есть творческий человек, который формирует новое знание. Предметы знаний в своей совокупности формируют научное сообщество. Она, в свою очередь, исторически развивается и организуется в различных социальных и профессиональных формах (академии, университеты, научно-исследовательские институты, лаборатории и т.д.).

С эпистемологической точки зрения можно утверждать, что субъект знаний — это социально-историческая сущность, реализующая социальные цели и осуществляющая познавательную деятельность на основе исторически сложившихся методов научного исследования.

Объектом познания является фрагмент реальности, находящийся в фокусе внимания исследователя. Проще говоря, объектом познания является то, что изучает ученый: электрон, клетка, семья. Это могут быть как явления и процессы объективного мира, так и субъективный мир человека: Мысли, душевное состояние, общественное мнение. Также объектом научного анализа могут быть как бы «побочные продукты» самой психической деятельности: художественные особенности литературного произведения, закономерности развития мифологии, религии и др. Объект объективен в отличие от собственных представлений исследователя о нем.

Иногда в эпистемологии вводится дополнительный термин «субъект познания», чтобы подчеркнуть нетривиальность формирования объекта науки. Предметом познания является определенный раздел или аспект объекта, который входит в сферу научного анализа. Объект знаний входит в науку через предмет знаний. Можно сказать, что объект познания — это проекция выбранного объекта на конкретные исследовательские задачи.

На странице рефераты по философии вы найдете много готовых тем для рефератов по предмету «Философия».

Здесь темы курсовых работ по философии

Читайте дополнительные лекции:

Подсистемы общества – сферы общественной жизни
Культура в условиях глобализации
Основные формы движения материи и проблема классификации наук — Проблема единства мира: история и современность
Философская сущность государства
Сёрен Обю Кьеркегор, датский теолог, философ, писатель
Создание универсального теплового двигателя (Джеймс Уатт, 1784) и становление машинного производства
Объективность знания и творческая деятельность
Л. Фейербах и его философия
Возрожденческий гуманизм и проблема индивидуальности — Переход от теоцентрического к антропологическому пониманию мира
Чарвака-Локаята – исторически первая философская материалистическая школа

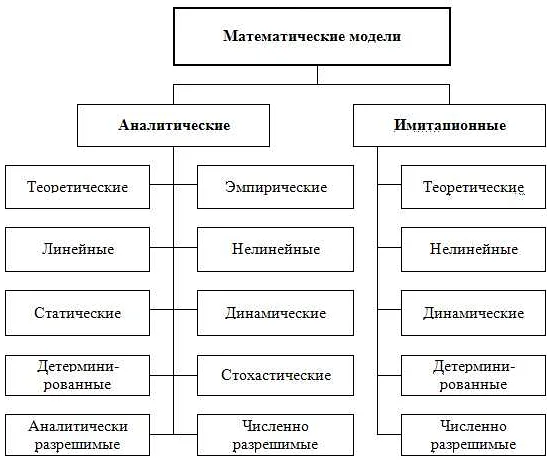
Виды математических моделей, классификация

Существует несколько классификаций математических моделей. Рассмотрим некоторые из них.

Формальная типология

Основа данной классификации — какие математические средства используются для создания модели. Для создания схем в формальной классификации часто используется прием дихотомии.

К известным типам дихотомии относятся:

Линейные	Нелинейные
Сосредоточенные	Распределенные
Детерминированные	Стохастические
Статические	Динамические
Дискретные	Непрерывные

Типология по методу представления объекта

В рамках данной классификации выделяют структурные и функциональные модели.

Структурная модель показывает объект как комплекс с механизмом и устройством функционирования.
Функциональные модели могут отражать поведение объекта, которое мы можем воспринимать внешне.

Эти парадигмы также имеют название «черные ящики».

Содержательные, а также формальные модели

Многие авторы, которые описывают процесс моделирования в математике, отмечают, что для начала нужно построить специальную образцовую конструкцию, так называемую содержательную модель.

Содержательная типология

В работах английского физика Рудольфа Эрнста Пайерлса можно найти некоторые типологии математических моделей, которые используются в физике и других естественных науках. Советские ученые Александр Горбань и Рэм Хлебопрос расширили классификацию Пайерлса

Данная типология акцентирует свое внимание на процессе выстраивания содержательной модели. Итак, существуют следующие типы математических моделей:

Гипотеза. Это пробное описание феноменов, автор которых либо верит в возможность их существования, либо считает это явление истинным. Такой, по мнению Пайерлса, является макет Солнечной системы от Птолемея, атомная модель Резерфорда, прототип Большого взрыва.
Феноменологическая модель. Этот тип содержит систему для описания феномена. Эта система обычно не особенно убедительна, не имеет достаточную аргументационную базу, плохо соотносится с существующими теориями. У феноменологических моделей временный статус. Ответ на вопрос феноменологической модели неизвестен, поэтому продолжается поиск истинных решений проблемы. К этому типу относятся макет теплорода.
Приближение. Если возможно построение уравнения, которое могло бы описать систему, это не значит, что его можно найти решения уравнения с помощью компьютерных программ. К таким уравнения относятся модели линейного отклика. Просто пример приближения — закон Ома.
Упрощение. В рамках данной модели убираются детали, которые могли бы повлиять на результат исследования (заметно и не контролируемо). Примером данного типа являются уравнения состояния Вандер-Ваальса, а также модели из физики жидкостей, твердого тела и т.д.
Эвристическая модель. Данная модель сохраняет подобие реальности, метод «слепого поиска» (через ошибки и пробы). Примером данной модели может быть измерение средней длины свободного пробега в кинетической теории.
Аналогия. Этот тип учитывает лишь некоторые особенности систем. Примером аналогии может быть исследование Гейзенберга о происхождении ядерных сил.
Мысленный эксперимент. Основа данного типа — предположение не на практике, не в результате реального эксперимента, а в опровержении какой-либо возможности в теории. Мысленный эксперимент часто использовал в своей работе Эйнштейн. В результате одного из мысленных экспериментов была выведена специальная теория относительности.
Демонстрация возможности. Основа данного типа — показать непротиворечивость возможности. Это своеобразные мысленные эксперименты, которые демонстрируют, что явление может согласоваться с базовыми теориями и непротиворечиво само по себе. Модель демонстрации возможности был использован для эксперимента геометрии Лобачевского.

Сложность моделируемой системы

Выделяются три уровня систем по сложности:

простые физические;
сложные физические;
биологические системы.

Советский академик Александр Андронов выделил три типа неустойчивых моделей:

Неустойчивые к преобразованию начальных требований.
Неустойчивые к небольшим преобразованиям условий, которые не вызывают никаких изменений в числе степеней свободы системы.
Неустойчивые к небольшим преобразованиям условий, которые вызывают изменения в числе степеней свободы системы.

Неустойчивые модели называют негрубыми. Устойчивые модели — мягкие.

Список литературы[]

Безручко Б. П., Смирнов Д.А. Математическое моделирование и хаотические временные ряды. — Саратов: ГосУНЦ «Колледж», 2005. — ISBN 5-94409-045-6. (см. ISBN )

Самарский А. А., Михайлов А. П. Математическое моделирование. Идеи. Методы. Примеры.. — 2-е изд., испр.. — М.: Физматлит, 2001. — ISBN 5-9221-0120-X. (см. ISBN )

Введение в математическое моделирование. Учебное пособие. Под ред. П. В. Трусова. — М.: Логос, 2004. — ISBN 5-94010-272-7. (см. ISBN )

Чимбал Б. Н. Математическое моделирование сложных систем в металлургии. — Москва: «Российские университеты» Кузбассвузиздат — АСТШ, 2004. — ISBN 5-202-00925-9. (см. ISBN )

Видео по теме:

Вопрос-ответ:

Что такое математические модели в компьютерной науке?

Математические модели — это специальные алгоритмы, которые используются в компьютерной науке для решения сложных математических задач.

Какие алгоритмы используются для построения математических моделей?

Для построения математических моделей используются алгоритмы, основанные на различных математических методах, таких как метод Ньютона, метод Монте-Карло, метод конечных элементов и т. д.

Что такое моделирование в компьютерной науке?

Моделирование — это процесс создания компьютерной математической модели, которая представляет собой абстрактную математическую модель реальной системы.

Какие задачи решаются с помощью компьютерных математических моделей?

Компьютерные математические модели могут решать самые различные задачи, включая анализ процессов в экономике, физике, медицине, биологии, генетике, геологии и т. д.

Какие разновидности математических моделей существуют в компьютерной науке?

Существуют различные типы математических моделей, такие как дискретные модели, непрерывные модели, стохастические модели, детерминистические модели и др.

Какими преимуществами обладают компьютерные математические модели?

Компьютерные математические модели имеют множество преимуществ, такие как ускорение процесса принятия решений, возможность исследования различных вариантов решения задачи, возможность получения результатов на основе различных входных параметров и др.

Проблемы и ограничения математических моделей

Математические модели — это упрощенные отображения реальных процессов и явлений. Хотя они могут помочь нам понять и предсказать поведение системы, но у них есть свои проблемы и ограничения.

Аппроксимация — Модели могут содержать значительные упрощения, которые могут не учитывать многие аспекты реального мира. Это может привести к неточности результатов.
Большое количество данных — Некоторые системы могут содержать так много переменных и данных, что моделирование их может быть чрезвычайно сложным и затратным.
Невозможность точного отображения — Некоторые системы могут быть настолько сложными, что их поведение не может быть точно предсказано в рамках математической модели, которая всегда является упрощенной версией реальности.
Неизвестные параметры — Некоторые параметры системы могут быть неизвестны или невозможно измерить, что может ухудшить результаты моделирования.

Несмотря на эти ограничения, математические модели остаются важным инструментом для изучения и предсказания поведения систем в науке, медицине, экономике и инженерии

Важно помнить, что модели являются лишь приближением реальности и всегда должны использоваться в сочетании с другими методами и исследованиями

Примеры применения математических моделей в реальной жизни

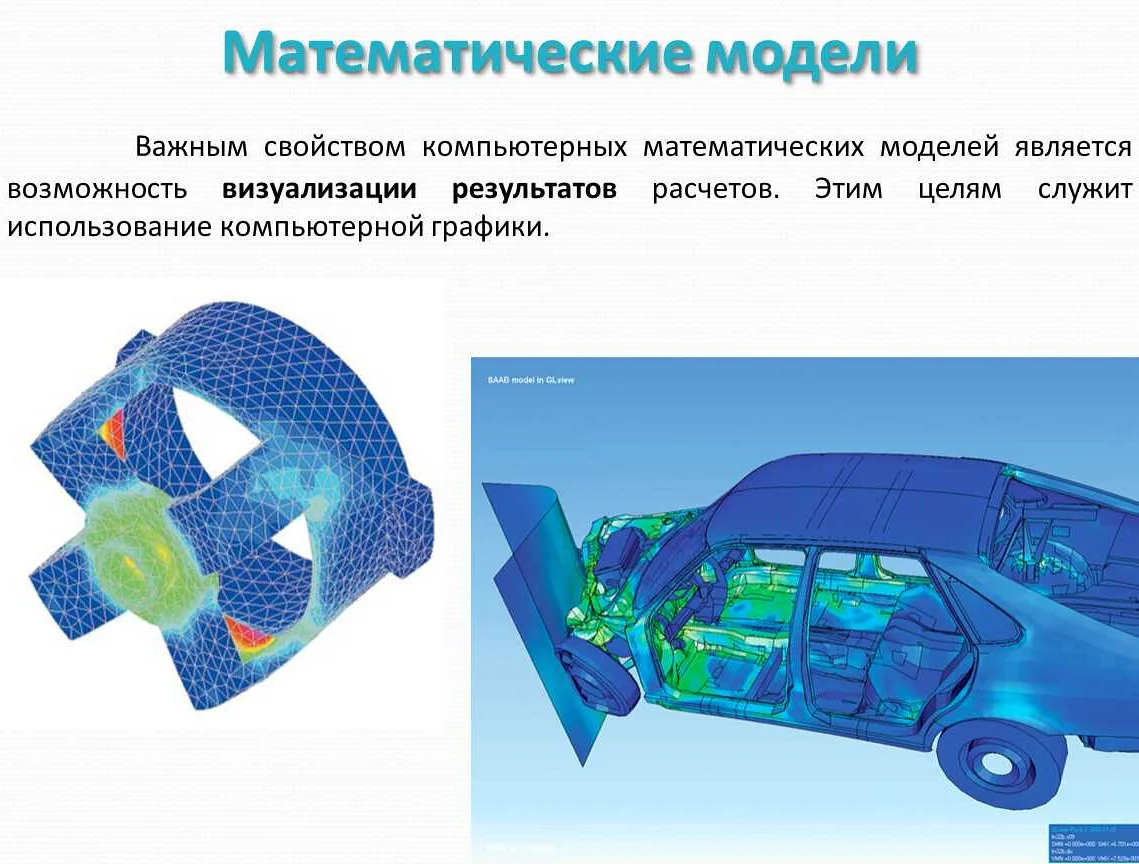
Математические модели находят своё применение во многих областях. Одним из ярких примеров является авиационная индустрия. Моделирование различных процессов и явлений позволяет оптимизировать полётные данные, что снижает расходы на топливо, повышает безопасность на борту, и улучшает качество обслуживания пассажиров. Кроме того, математические модели используются для проектирования и испытания самолётов.

Ещё одним из примеров использования математических моделей является медицинская диагностика. Моделирование различных физиологических процессов позволяет проводить компьютерную диагностику рака, сердечно-сосудистых заболеваний, инфаркта миокарда, и других заболеваний. При этом, точность результатов намного выше, чем при обычных методах диагностики.

Математические модели также широко применяются в производственных процессах. Они помогают управлять складскими запасами, контролировать производственные циклы, оптимизировать работу оборудования, учитывать влияние климатических условий, и многое другое. Это повышает эффективность производств, снижает затраты на производство, и повышает качество продукции.

Среди других областей, где применяются математические модели, можно выделить:
Экономика и финансы, где моделируются различные финансовые процессы и позволяют принимать обоснованные инвестиционные решения;
Геология и геофизика, где моделирование позволяет лучше понимать поведение различных геологических процессов, в том числе землетрясений и вулканических извержений;
Транспорт и логистика, где математические модели позволяют оптимизировать маршруты перевозок и снижать затраты на транспортировку грузов;
Информационные технологии, где математические модели применяются для разработки алгоритмов и программных решений.

Универсальность моделей[]

Математические модели обычно обладают важным свойством универсальности:
принципиально разные реальные явления могут описываться одной и той же
математической моделью. Скажем, гармонический осциллятор описывает не только
поведение груза на пружине, но и другие колебательные процессы, зачастую имеющие
совершенно иную природу: малые колебания маятника, колебания уровня жидкости в
U{\displaystyle U}-образном сосуде, изменение силы тока в колебательном контуре или колебания
популяций биологических видов. Таким образом, изучая одну математическую
модель, мы изучаем сразу целый класс описываемых ею явлений.

2 Виды математического моделирования

2.1 Аналитическое моделирование

Наиболее строгое исследование базируется, обычно, на аналитической математической модели. В этом случае модельный слой реализуется посредством математических выражений, описывающих эволюцию системы.

2.2 Физическое моделирование

Полученную математическую модель нужно сопоставить с экспериментальными данными, верифицировать её. Для этого можно создать модель, аналогичную физической или технической системе.
Физическая модель может быть и виртуальной. Например, можно построить модель сети передачи данных, используя образы операционных систем маршрутизаторов и коммутаторов.

2.3 Имитационное моделирование

С развитием компьютерной техники появилась возможность задавать модельную реализацию не в виде математического описания, а в виде некоторого алгоритма.
Такого типа модели получили название имитационных моделей, а сам подход получил название имитационного моделирования.
Имитационная модель играет двоякую роль.
- Отлаженная и проверенная на экспериментальных данных и физической модели имитационная модель сама по себе может служить целям верификации математической модели.
- С другой стороны, имитационная модель позволяет более эффективно, чем математическая модель, исследовать поведение моделируемой системы при разных вариантах входных данных.

2.4 Статистическое моделирование

К данному типу моделирования относят модели, которые реализуются посредством методов машинного обучения.
Его можно разделить на несколько подходов.

2.4.1 Суррогатное моделирование

Другие названия: аппроксимационные модели, модели поверхности отклика, метамодели, модели чёрного ящика (см. Суррогатное моделирование).
В этом подходе модельный слой известен и даже имеет реализацию (чаще всего в виде аналитической модели).
Для многих реальных проблем моделирование может занять достаточно продолжительное время. Крайне затруднены такие (достаточно рутинные) задачи, как оптимизация решений, исследование пространства решений, анализ чувствительности и анализ «что, если» становятся невозможными, поскольку они требуют тысяч или миллионов оценок моделирования.
Для упрощения исследования строятся модели, которые имитируют поведение исходной модели настолько близко, насколько это возможно, в то время как вычислительно дёшевы. Суррогатные модели строятся с использованием подхода, основанного на данных

Точная внутренняя работа кода моделирования не предполагается известной (или даже понятой), важно только поведение ввода–вывода (приготовления–измерения). Модель строится на основе моделирования реакции на ограниченное количество (порой достаточно большое) выбранных точек данных

Научная задача суррогатного моделирования заключается в создании суррогата, который является максимально точным, используя как можно меньше оценок моделирования.

Процесс состоит из следующих основных этапов, которые могут чередоваться:
выбор образца;
построение суррогатной модели и оптимизация параметров модели;
оценка точности суррогата.

2.4.2 Обработка больших данных

Применяется, когда отсутствует модель как таковая и природа истинной функции априори неизвестна, поэтому неясно, какая суррогатная модель будет наиболее точной. Кроме того, непонятно, как получить наиболее надёжные оценки точности данного суррогата. В данном случае модельный слой заменяется догадками исследователя. (см. Data Science и научное мышление).

Заметим, что такого типа модели известны многим исследователям. Когда задействована только одна расчётная переменная, процесс построения суррогатной модели называется подгонкой кривой.

Пример №8: Математическая модель генетического алгоритма

Генетический алгоритм – это метод оптимизации, вдохновленный принципами эволюционного процесса в природе. Он использует механизмы наследования, мутации и отбора, чтобы создавать новые решения на основе уже существующих.

Математическая модель генетического алгоритма состоит из нескольких компонентов: начальной популяции, функции пригодности, операторов отбора, кроссинговера и мутации.

Начальная популяция – это набор случайных решений, которые служат отправной точкой для оптимизации.
Функция пригодности – это мера качества каждого решения в популяции. Она определяет, насколько хорошо решение соответствует заданным требованиям.
Операторы отбора – это методы выбора родительских решений, которые будут использоваться для создания новых решений в следующем поколении.
Кроссинговер – это оператор, который комбинирует информацию от родительских решений для создания потомства.
Мутация – это оператор, который случайным образом изменяет некоторые компоненты решения.

Совмещение этих компонентов позволяет генетическому алгоритму находить оптимальные решения в задачах оптимизации. Он может быть использован для решения самых разнообразных задач, таких как поиск оптимальной конфигурации оборудования или настройка параметров алгоритма машинного обучения.

Математическая модель генетического алгоритма может быть реализована на языке программирования, таком как Python или Java, путем написания соответствующего кода для каждого из компонентов. Такой код позволяет автоматизировать процесс оптимизации и получать быстрые и точные результаты.

Пример №7: Математическая модель экономического цикла

Математическая модель экономического цикла — это математическая модель, которая описывает повторяемые колебания экономической активности во времени. Экономический цикл — это периодическое изменение конъюнктуры национальной экономики, которое характеризуется заметным изменением темпа роста производства и уровня занятости. Модель экономического цикла позволяет исследовать влияние различных экономических факторов на периоды бума и спада в экономике.

Математическая модель экономического цикла может быть представлена в виде системы дифференциальных уравнений, которые описывают изменение промышленного выпуска, инвестиций, занятости и других экономических показателей во времени. Для создания такой модели необходимо провести сбор и анализ данных о состоянии экономики, чтобы определить основные факторы, влияющие на экономический цикл.

Математическая модель экономического цикла может быть использована для прогнозирования экономических кризисов, а также для разработки эффективных мер по их предотвращению. Она может помочь правительству и бизнесу принимать обоснованные решения в сфере экономики, учитывая возможные последствия на будущее.

Создание математической модели экономического цикла требует глубокого понимания экономических закономерностей, а также высокой квалификации в области математики и статистики. Для успешного создания такой модели необходимо строго следовать этапам моделирования и использовать точные и достоверные данные.

1 Классификация методов моделирования

Моделирование как дисциплина охватывает разные типы модельных подходов. С нашей точки зрения эти подходы можно схематически описать единым образом.
Исследовательская структура состоит из операциональных и теоретических частей.
Операциональные части представлены процедурами приготовления системы и измерения. Также возможно описание операциональных частей как входных и выходных данных.
Теоретическая часть состоит из двух слоёв: модельного слоя и слоя реализации.
- Модельный слой является основным и задаёт собственно исследуемую модель.
- Слой реализации описывает конкретную структуру эволюции системы. В зависимости от типа реализации, можно получать разные виды моделей:
  - реализация — математические выражения: аналитические математические модели;
  - реализация — аналоговая система: физическая модель;
  - реализация — алгоритм: имитационные модели;
  - реализация — аппроксимация поведения: суррогатная модель.
Каждый тип моделей имеет свою область применимости, свои преимущества и недостатки.
Использование всего спектра моделей позволяет наиболее глубокое и всестороннее исследование моделируемой системы.

5.4.3. Моделирование и проблема истины

Интересен вопрос о том, какую роль играет само моделирование, то есть построение моделей, их изучение и проверка в процессе доказательства истинности и поисков истинного знания.

Что же следует понимать под истинностью модели? Если истинность вообще -соотношение наших знаний объективной действительности , то истинность модели означает соответствие модели объекту, а ложность модели -отсутствие такого соответствия. Такое определение является необходимым, но недостаточным

Требуются дальнейшие уточнения, основанные на принятие во внимание условий, на основе которых модель того или иного типа воспроизводит изучаемое явление. Например, условия сходства модели и объекта в математическом моделировании, основанном на физических аналогиях, предполагающих при различии физических процессов в модели и объекте тождество математической формы, в которой выражаются их общие закономерности, являются более общими, более абстрактными

Таким образом, при построении тех или иных моделей всегда сознательно отвлекаются от некоторых сторон, свойств и даже отношений, в силу чего, заведомо допускается несохранение сходства между моделью и оригиналом по ряду параметров, которые вообще не входят в формулирование условий сходства Так планетарная модель атома Резерфорда оказалась истинной в рамках(и только в этих рамках) исследования электронной структуры атома, а модель Дж.Дж. Томпсона оказалась ложной, так как ее структура не совпадала с электронной структурой. Истинность — свойство знания, а объекты материального мира не истинны, не ложны, просто существуют. Можно ли говорить об истинности материальных моделей, если они — вещи, существующие объективно, материально? Этот вопрос связан с вопросом: на каком основании можно считать материальную модель гносеологическим образом? В модели реализованы двоякого рода знания:

знание самой модели (ее структуры, процессов, функций) как системы, созданной с целью воспроизведения некоторого объекта,

теоретические знания, посредством которых модель была построена.

Имея в виду именно теоретические соображения и методы, лежащие в основе построения модели, можно ставить вопросы о том, на сколько верно данная модель отражает объект и насколько полно она его отражает. В таком случае возникает мысль о сравнимости любого созданного человеком предмета с аналогичными природными объектами и об истинности этого предмета. Но это имеет смысл лишь в том случае, если подобные предметы создаются со специальной целью изобразить, скопировать, воспроизвести определенные черты естественного предмета.

Таким образом, можно говорить о том, истинность присуща материальным моделям:

в силу связи их с определенными знаниями;

в силу наличия (или отсутствия) изоморфизма ее структуры со структурой моделируемого процесса или явления,

в силу отношения модели к моделируемому объекту, которое делает ее частью познавательного процесса и позволяет решать определенные познавательные задачи.

Важнейший аспект, связанный с ролью моделирования в установлении истинности той или иной формы теоретического знания. Здесь модель можно рассматривать не только как орудие проверки того, действительно ли существуют такие связи, отношения, структуры, закономерности, которые формулируются в данной теории и выполняются в модели Успешная работа модели есть практическое доказательство истинности теории, то есть это часть экспериментального доказательства истинности этой теории