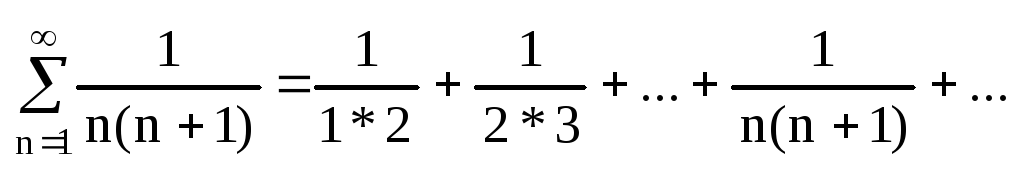Комплексные числа в математике: определение, примеры решения и свойства

Основные понятия

Действительная часть комплексного числа обозначается Re(z) или Real(z), а мнимая часть — Im(z) или Imag(z). Комплексное число z = a + bi можно представить на комплексной плоскости, где ось абсцисс соответствует действительной оси, а ось ординат — мнимой оси. Такая плоскость называется комплексной плоскостью.

Комплексные числа можно складывать, вычитать, умножать и делить. Сложение и вычитание комплексных чисел производится покомпонентно: (a + bi) + (c + di) = (a + c) + (b + d)i, (a + bi) — (c + di) = (a — c) + (b — d)i. Умножение комплексных чисел производится по формуле комплексного умножения: (a + bi) * (c + di) = ac + adi + bci – bd = (ac – bd) + (ad + bc)i.

Комплексные числа также имеют свою алгебраическую форму, которая выражается в виде z = mod(z) * e^(i * arg(z)), где mod(z) — модуль комплексного числа, равный корню из суммы квадратов вещественной и мнимой части числа (|z| = sqrt(a^2 + b^2)), а arg(z) — аргумент комплексного числа, выражающийся как арктангенс отношения мнимой части к вещественной (arg(z) = arctan(b/a)).

Алгебраическая и геометрическая формы записи

z = a + bi

где a — действительная часть комплексного числа, b — мнимая часть числа, а i — мнимая единица, которая определяется следующим образом: i = √(-1).

Алгебраическая форма записи позволяет выполнять арифметические операции с комплексными числами, такие как сложение, вычитание, умножение, деление.

Геометрическая форма записи представляет комплексное число в виде точки на комплексной плоскости. Комплексная плоскость представляет собой плоскость, в которой действительная ось (горизонтальная ось) соответствует действительной части числа, а мнимая ось (вертикальная ось) — мнимой части:

z = r(cosθ + isinθ)

где r — модуль комплексного числа (расстояние от начала координат до точки), а θ — аргумент комплексного числа (угол между положительным направлением действительной оси и лучом, проведенным от начала координат до точки).

Геометрическая форма записи комплексного числа позволяет наглядно представить его на комплексной плоскости и выполнять операции с комплексными числами, такие как умножение, деление, возведение в степень.

Комплексное сопряжение

Комплексное сопряжение числа z обозначается как z*, и определяется следующим образом:

Операция	Запись	Результат
Действительная часть	Re(z)	Re(z*) = Re(z)
Мнимая часть	Im(z)	Im(z*) = -Im(z)
Модуль	\|z\|	\|z*\| = \|z\|
Аргумент	arg(z)	arg(z*) = -arg(z)

Комплексное сопряжение числа z позволяет найти его сопряженное комплексное число z*

Важно отметить, что при сопряжении части числа меняют знак, а модуль и аргумент остаются неизменными

Арифметические операции с комплексными числами

Комплексные числа можно складывать, вычитать, умножать и делить, как и обычные действительные числа. Однако, при выполнении арифметических операций с комплексными числами мы также учитываем их мнимые части.

Сложение комплексных чисел выполняется путем сложения их действительных и мнимых частей по отдельности. Например, если у нас есть два комплексных числа z₁ = a + bi и z₂ = c + di, то их сумма будет равна z₁ + z₂ = (a + c) + (b + d)i.

Вычитание комплексных чисел также выполняется путем вычитания их действительных и мнимых частей по отдельности. Например, если у нас есть два комплексных числа z₁ = a + bi и z₂ = c + di, то их разность будет равна z₁ — z₂ = (a — c) + (b — d)i.

Умножение комплексных чисел выполняется с учетом свойства i2 = -1. Если у нас есть два комплексных числа z₁ = a + bi и z₂ = c + di, то их произведение будет равно z₁ * z₂ = (ac — bd) + (ad + bc)i.

Деление комплексных чисел выполняется с использованием сопряженных чисел и учетом свойства i2 = -1. Если у нас есть два комплексных числа z₁ = a + bi и z₂ = c + di, то их частное будет равно z₁ / z₂ = ((ac + bd) / (c2 + d2)) + ((bc — ad) / (c2 + d2))i.

Таким образом, арифметические операции с комплексными числами выполняются аналогично операциям с обычными действительными числами, но с учетом их действительных и мнимых частей.

Связанные определения[]

Комплексная переменная обычно обозначается z{\displaystyle z}.
Пусть x{\displaystyle x} и y{\displaystyle y} суть вещественные числа, такие, что z=x+iy{\displaystyle z=x+iy}.
Тогда

Числа x=ℜ(z){\displaystyle x=\Re (z)} или Re⁡(z){\displaystyle \operatorname {Re} (z)} и y=ℑ(z){\displaystyle y=\Im (z)} или Im⁡(z){\displaystyle \operatorname {Im} (z)} называются соответственно вещественной (Real) и мнимой (Imaginary) частями z{\displaystyle z}
Если x=0{\displaystyle x=0}, то z{\displaystyle z} называется мнимым или чисто мнимым.

.
Число |z|=x2+y2{\displaystyle |z|={\sqrt {x^{2}+y^{2}}}} называется модулем числа z{\displaystyle z}. Для вещественного числа модуль совпадает с его абсолютной величиной. Некоторые свойства модуля:

|z|⩾{\displaystyle |z|\geqslant 0\,}, причём |z|={\displaystyle |z|=0\,} тогда и только тогда, когда z={\displaystyle z=0\,}

|z1+z2|⩽|z1|+|z2|{\displaystyle |z_{1}+z_{2}|\leqslant |z_{1}|+|z_{2}|\,} (неравенство треугольника)

|z1⋅z2|=|z1|⋅|z2|{\displaystyle |z_{1}\cdot z_{2}|=|z_{1}|\cdot |z_{2}|\,}

|z1z2|=|z1||z2|{\displaystyle |z_{1}/z_{2}|=|z_{1}|/|z_{2}|\,}
Угол φ{\displaystyle \varphi } такой, что: cos⁡φ=x|z|{\displaystyle \cos \varphi ={\frac {x}{|z|}}} и sin⁡φ=y|z| {\displaystyle \sin \varphi ={\frac {y}{|z|}}~~}, называется аргументом z{\displaystyle z}. Для комплексного нуля значение аргумента не определено, для ненулевого числа z{\displaystyle z} аргумент определяется с точностью до 2kπ{\displaystyle 2k\pi }, где k{\displaystyle k} — любое целое число.

Сопряжённые числа

Если комплексное число z=x+iy{\displaystyle z=x+iy}, то число z¯=x−iy{\displaystyle {\bar {z}}=x-iy} называется сопряжённым (или комплексно сопряжённым) к z{\displaystyle z}.

Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.

z¯¯=z{\displaystyle {\bar {\bar {z}}}=z} (сопряжённое к сопряжённому есть исходное)
z⋅z¯=|z|2{\displaystyle z\cdot {\bar {z}}=|z|^{2}}
z1±z2¯=z1¯±z2¯{\displaystyle {\overline {z_{1}\pm z_{2}}}={\bar {z_{1}}}\pm {\bar {z_{2}}}}
z1⋅z2¯=z¯1⋅z¯2{\displaystyle {\overline {z_{1}\cdot z_{2}}}={\bar {z}}_{1}\cdot {\bar {z}}_{2}}
z1z2¯=z¯1z¯2{\displaystyle {\overline {z_{1}/z_{2}}}={\bar {z}}_{1}/{\bar {z}}_{2}}

Обобщение: p(z)¯=p(z¯){\displaystyle {\overline {p(z)}}=p({\bar {z}})}, где p(z){\displaystyle p(z)} — произвольный комплексный многочлен.

|z¯|=|z|{\displaystyle |{\bar {z}}|=|z|} (модуль сопряжённого числа такой же, как у исходного)

Визуальное понимание отрицательных и комплексных чисел

Уравнение x^2 = 9 на самом деле означает следующее:

или

Какое преобразование x, применяемое дважды, превращает 1 в 9?

Есть два ответа: «x = 3» и «x = -3». То есть, вы можете «масштабировать в» 3 раза или «масштабировать в 3 раза и перевернуть» (переворачивание или взятие обратного результата — всё это интерпретации умножения на отрицательную единицу).

А теперь давайте подумаем об уравнении x^2 = -1, которое можно записать так:

Какое преобразование x, применяемое дважды, превращает 1 в -1? Хм.

Мы не можем умножить дважды положительное число, потому что результат будет положительным.
Мы не можем умножить дважды отрицательное число, потому что результат опять будет положительным.

А как насчёт… вращения! Звучит, конечно, необычно, но что если представить х как «поворот 90 градусов», тогда применив х дважды, мы совершим поворот на 180 градусов на координатной оси, и 1 обернется в -1!

Вот это да! И если мы еще немного над этим поразмышляем, то мы можем совершить два оборота в противоположном направлении, и также перейти с 1 на -1. Это «отрицательное» вращение или умножение на -i:

Если мы дважды умножим на-i, то при первом умножении получим -i из 1, а при втором -1 из -i. Так что на самом деле существует два квадратных корня -1: i и -i.

Это довольно круто! У нас есть что-то вроде решения, но что оно означает?

i — это «новая мнимая размерность» для измерения числа
i (или -i) — это то, чем «становятся» числа при вращении
Умножение на i — это вращение на 90 градусов против часовой стрелки
Умножение на -i — это вращение на 90 градусов по часовой стрелке.
Двойное вращение в любом из направлений дает -1: оно опять возвращает нас к «обычной» размерности положительных и отрицательных чисел (ось x).

Все числа 2-мерные. Да, это трудно принять, но древним римлянам было бы также трудно принять десятичные дроби или деление в столбик. (Как это так, между 1 и 2 есть еще числа?). Выглядит странно, как и любой новый способ мыслить в математике.

Мы спросили «Как превратить 1 в -1 в два действия?» и нашли ответ: повернуть 1 на 90 градусов дважды. Довольно странный, новый способ мыслить в математике. Но очень полезный. (Между прочим, эта геометрическая интерпретация комплексных чисел появилась только десятилетия спустя после открытия самого числа i).

Также, не забывайте, что принятие оборота против часовой стрелки за положительный результат — это сугубо человеческая условность, и всё могло бы быть совсем по-другому.

Примеры использования комплексных чисел в реальной жизни

Комплексные числа находят широкое применение в различных областях науки и техники. Вот несколько примеров:

Электрические цепи: Комплексные числа используются для анализа и моделирования электрических цепей. Они позволяют учитывать фазовые сдвиги и амплитуды сигналов, а также рассчитывать электрические параметры цепей.

Теория сигналов: Комплексные числа применяются для анализа и обработки сигналов в области радиотехники, телекоммуникаций и цифровой обработки сигналов. Они позволяют представлять сигналы в комплексной плоскости и проводить операции с ними, например, фильтрацию и модуляцию.

Квантовая механика: Комплексные числа широко используются в квантовой механике для описания состояний квантовых систем. Они позволяют представлять волновые функции и проводить операции с ними, например, суперпозицию и измерение.

Аэродинамика: Комплексные числа применяются для моделирования и анализа аэродинамических процессов. Они позволяют учитывать фазовые сдвиги и амплитуды колебаний в аэродинамических потоках, а также рассчитывать характеристики аэродинамических объектов.

Теория управления: Комплексные числа используются для анализа и моделирования динамических систем в теории управления. Они позволяют представлять передаточные функции и амплитудно-фазовые характеристики систем, а также рассчитывать устойчивость и переходные процессы.

Таким образом, комплексные числа играют важную роль в различных областях науки и техники, позволяя представлять и анализировать системы с учетом их фазовых и амплитудных характеристик.

Действия над комплексными числами.

1.

сложение. z 1 +z 2 =(x1+iy1)+
(x2+iy2)=(x1+x2)+i(y1+y2);

2
.
вычитание. z 1 -z 2 =(x1+iy1)-
(x2+iy2)=(x1-x2)+i(y1-y2);

3.

умножение.
z 1 z 2 =(x1+iy1)*(x2+iy2)=x1x2+i(x1y2+x2y1+iy1y2)=(x1x2-y1y2)+i(x1y2+x2y1);

4
.
деление. z 1 /z 2 =(x1+iy1)/(x2+iy2)=/=

Два
комплексных числа, которые отличаются
только знаком мнимой единицы, т.е. z=x+iy
(z=x-iy),
называются сопряженными.

Произведение.

z1=r(cos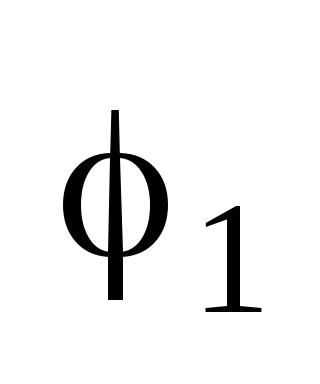+isin);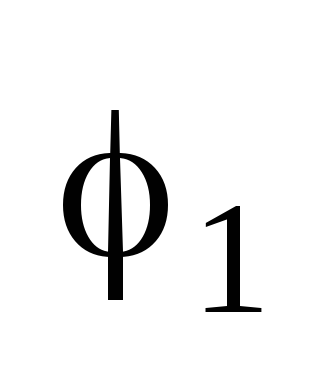
z2=r(cos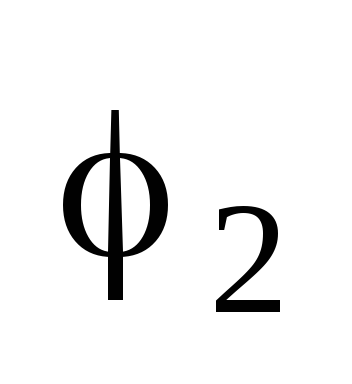+isin).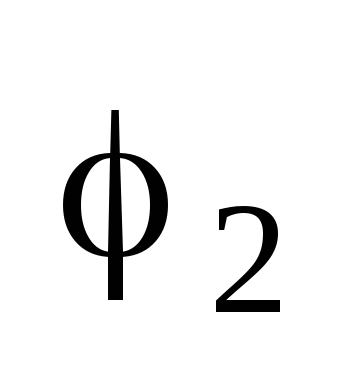

То
произведение z1*z2
комплексных чисел находится:
,
т.е. модуль произведения равен произведению
модулей, а аргумент произведения равен
сумме аргументов сомножителей.

;
;

Частное.

Если комплексные числа заданы в
тригонометрической форме.

Если комплексные числа заданы в
показательной форме.

Возведение
в степень.

1.

Комплексное число задано в алгебраической

форме.

z=x+iy,
то z n
находим по формуле
бинома Ньютона
:

—
число сочетаний из n
элементов по m
(число способов, сколькими можно взять
n
элементов
из
m).

;
n!=1*2*…*n; 0!=1;
.

Применяем
для комплексного числа.

В
полученном выражении нужно заменить
степени i
их значениями:

i 0 =1
Отсюда,
в общем случае получаем: i 4k =1

i 1 =i i 4k+1 =i

i 2 =-1 i 4k+2 =-1

i 3 =-i i 4k+3 =-i

Пример
.

i 31 =
i 28
i 3 =-i

i 1063 =
i 1062
i=i

2.
тригонометрической

форме.

z=r(cos+isin),
то

—
формула
Муавра
.

Здесь
n
может быть как “+” так и “-” (целым).

3.

Если комплексное число задано в
показательной

форме:

Извлечение
корня.

Рассмотрим
уравнение:
.

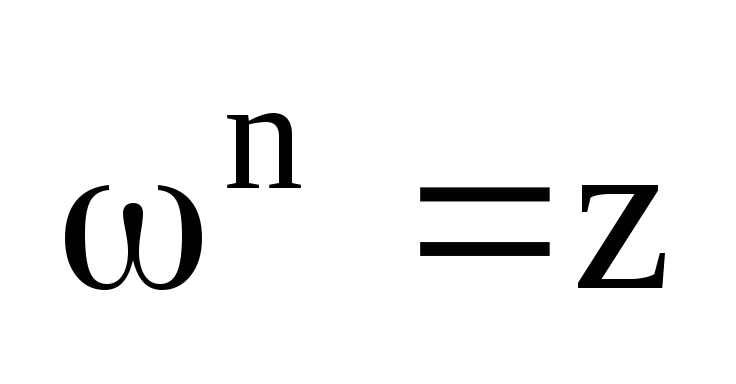Его
решением будет корень n–ой степени из
комплексного числа z:
.

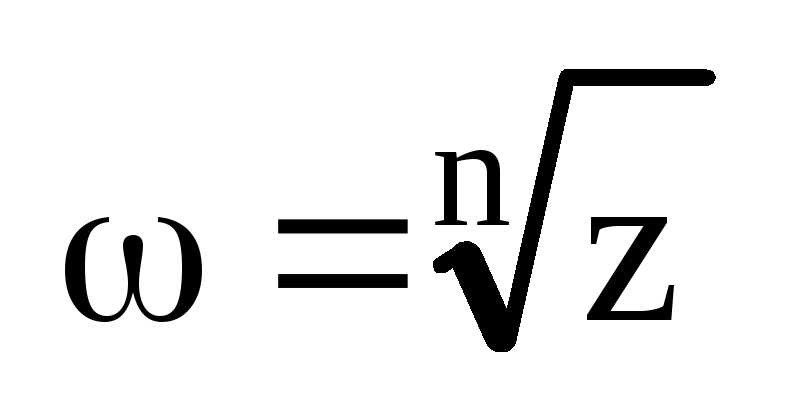Корень
n–ой степени из комплексного числа z
имеет ровно n решений (значений). Корень
из действующего числа n-ой степени имеет
только одно решение. В комплексных – n
решений.

Если
комплексное число задано в тригонометрической

форме:

z=r(cos+isin),
то корень n-ой степени от z находится по
формуле:

,
где к=0,1…n-1.

Презентация на тему: » НАЧАЛО. Наши первоначальные представления о числе и форме относятся к очень отдаленной эпохе древнего каменного века – палеолита.» — Транскрипт:

НАЧАЛО. Наши первоначальные представления о числе и форме относятся к очень отдаленной эпохе древнего каменного века – палеолита.

Не так уж и много приходилось считать первобытному человеку. Но был у него свой первобытный «компьютер» – десять пальцев на руках. Загибал человек пальцы – складывал. Разгибал – вычитал. На пальцах считать удобно, только результат счета хранить нельзя. Не станешь же целый день ходить с загнутыми пальцами. И человек догадался: для счета можно использовать все, что попадется под руку – камешки, палочки, косточки …. Потом стали узелки на веревке завязывать, делать зарубки на палках.

Около пяти тысяч лет назад люди догадались, что числа можно записывать не просто зарубками – единицами, а по разрядам. Это было очень важным открытием. Жизнь заставляла их учиться быстрее. Нужно было разбивать участки земли, отводить воду из рек, прорывать каналы в тех местах, где поля были выше реки, надо было поднимать воду наверх. Приходилось ломать голову над тем, как облегчить эту тяжелую работу. Постепенно из набора просто отдельных правил математика стала превращаться в науку.

Настоящей наукой математика стала только у древних греков. Это был удивительно талантливый народ, у которого есть чему поучиться даже сейчас, тысячи лет спустя. Каждое правило греческие математики старались объяснить, доказать, что оно действительно верное. Для этого они спорили друг с другом, рассуждали, старались найти в рассуждениях ошибки. Из правил складывались законы, из законов – наука математика.

ЦИФРЫ Италия Южная Америка Индия С Востока ГрецияАнглия Римская Империя Из какой страны к нам пришли цифры?

Индийские ученые сделали одно из важнейших в математике открытий. Они изобрели позиционную систему счисления – способ записи и чтения чисел, которым теперь пользуется весь мир.

Чтобы назвать большое число, индийцам приходилось после каждой цифры произносить название разряда. Это было громоздко, неудобно, и индийцы стали поступать иначе. Например, число читали так: два, семь, восемь, три, девять, шесть, – сколько цифр – столько слов. А если в числе не было какого-нибудь разряда, как например, в числах 206 или 7013, то вместо названия цифры говорили слово «пусто». Чтобы не получилось путаницы, при записи на месте «пусто» разряда ставили точку.

Позднее вместо точки стали рисовать кружок, который на языке хинди назывался «сунья», что значит «пустое место». Арабские математики перевели это слово на свой язык. Вместо «сунья» они стали говорить «сифр», а это уже знакомое нам слово. Слово «цифра» по наследству от арабов досталось и нам.

ЧИСЛА дробныеотрицательные чётные и нечётные действительныенатуральныерациональныеиррациональныеположительныемнимыецелые Какие числа изучают в школе?

Страна Натуральных Чисел – это необыкновенная, замечательная страна, в которой живут, трудятся и властвуют натуральные числа. Интерес к изучению чисел возник у людей в глубокой древности, и вызван он был не только практической необходимостью. Привлекала необычайная магическая сила числа, которым можно выразить количество любых предметов. Натуральными числами обозначались и боги, и космос, и люди, и их взаимоотношения

Поэтому изучению натуральных чисел уделялось и сейчас уделяется особое внимание

«Фундаментом математических знаний, от которого зависит прочность дальнейшего математического образования, является знание принципа образования натурального ряда чисел», – говорил выдающийся педагог В.А.Сухомлинский.

Изображение числовых множеств на координатной прямой

На практике удобно пользоваться геометрическими образами числовых множеств – их изображениями на . Например, при решении неравенств
, в которых необходимо учитывать ОДЗ, приходится изображать числовые множества, чтобы найти их пересечение и/или объединение. Так что полезно будет хорошо разобраться со всеми нюансами изображения числовых множеств на координатной прямой.

Известно, что между точками координатной прямой и действительными числами существует взаимно однозначное соответствие, что означает, что сама координатная прямая представляет собой геометрическую модель множества всех действительных чисел R
. Таким образом, чтобы изобразить множество всех действительных чисел, надо начертить координатную прямую со штриховкой на всем ее протяжении:

А часто даже не указывают начало отсчета и единичный отрезок:

Теперь поговорим про изображение числовых множеств, представляющих собой некоторое конечное число отдельных чисел. Для примера, изобразим числовое множество {−2, −0,5, 1,2}
. Геометрическим образом данного множества, состоящего из трех чисел −2
, −0,5
и 1,2
будут три точки координатной прямой с соответствующими координатами:

Отметим, что обычно для нужд практики нет необходимости выполнять чертеж точно

Часто достаточно схематического чертежа, что подразумевает необязательное выдерживание масштаба, при этом важно лишь сохранять взаимное расположение точек относительно друг друга: любая точка с меньшей координатой должна быть левее точки с большей координатой. Предыдущий чертеж схематически будет выглядеть так:

Отдельно из всевозможных числовых множеств выделяют числовые промежутки (интервалы, полуинтервалы, лучи и т.д.), что представляют их геометрические образы, мы подробно разобрались в разделе . Здесь не будем повторяться.

И остается остановиться лишь на изображении числовых множеств, представляющих собой объединение нескольких числовых промежутков и множеств, состоящих из отдельных чисел. Здесь нет ничего хитрого: по смыслу объединения в этих случаях на координатной прямой нужно изобразить все составляющие множества данного числового множества. В качестве примера покажем изображение числового множества (−∞, −15)∪{−10}∪[−3,1)∪
{log 2 5, 5}∪(17, +∞)
:

И остановимся еще на достаточно распространенных случаях, когда изображаемое числовое множество представляет собой все множество действительных чисел, за исключением одной или нескольких точек. Такие множества частенько задаются условиями типа x≠5
или x≠−1
, x≠2
, x≠3,7
и т.п. В этих случаях геометрически они представляют собой всю координатную прямую, за исключением соответствующих точек. Иными словами, из координатной прямой нужно «выколоть» эти точки. Их изображают кружочками с пустым центром. Для наглядности изобразим числовое множество, соответствующее условиям (это множество по сути есть ):

Подведем итог. В идеале информация предыдущих пунктов должна сформировать такой же взгляд на запись и изображение числовых множеств, как и взгляд на отдельные числовые промежутки: запись числового множества сразу должна давать его образ на координатной прямой, а по изображению на координатной прямой мы должны быть готовы с легкостью описать соответствующее числовое множество через объединение отдельных промежутков и множеств, состоящих из отдельных чисел.

Список литературы.

Алгебра:
учеб. для 8 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
Мордкович А. Г.
Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.

Ряды. Числовые ряды.

Пусть
переменная а принимает последовательно
значения а 1 ,а 2 ,а 3 ,…,а n .
Такое перенумерованное множество чисел
называется последовательностью. Она
бесконечна.

Числовым
рядом называется выражение а 1 +а 2 +а 3 +…+а n +…=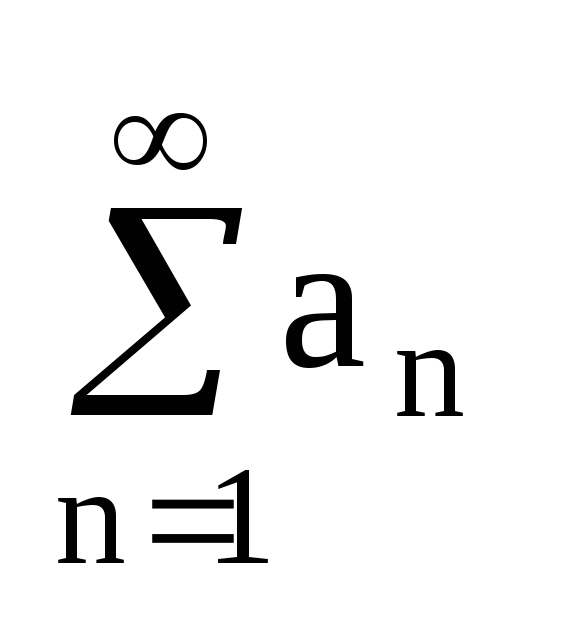. Числа а 1 ,а 2 ,а 3 ,…,а n
– члены ряда.

Например.

а 1
– первый член ряда.

а n
– n-ый или общий член ряда.

Ряд
считается заданным, если известен n-ый
(общий член ряда).

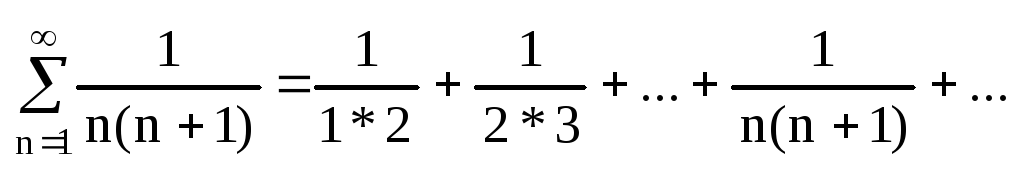
Числовой
ряд имеет бесконечное число членов.

Числители
– арифметическая
прогрессия

(1,3,5,7…).

n-ый
член находится по формуле а n =а 1 +d(n-1);
d=а n -а n-1 .

Знаменатель
– геометрическая
прогрессия
.
b n =b 1 q n-1 ;
.

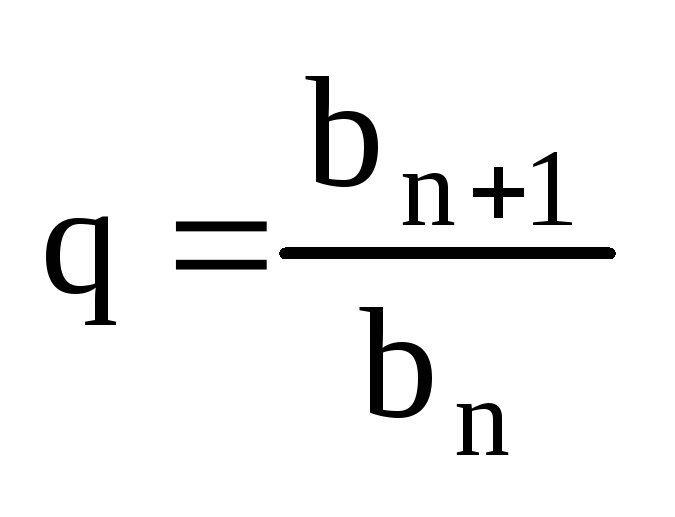Рассмотрим
сумму первых n членов ряда и обозначим
ее Sn.

Sn=а1+а2+…+а n .

Sn
– n-ая частичная сумма ряда.

Рассмотрим
предел:

S
— сумма ряда.

Ряда
сходящийся

,
если этот предел конечен (конечный
предел S существует).

Ряд
расходящийся

,
если этот предел бесконечен.

В
дальнейшем наша задача заключается в
следующем: установить
какой ряд.

Одним
из простейших, но часто встречающихся
рядов является геометрическая прогрессия.

,
C=const.

Геометрическая
прогрессия является
сходящимся

рядом
,
если
,
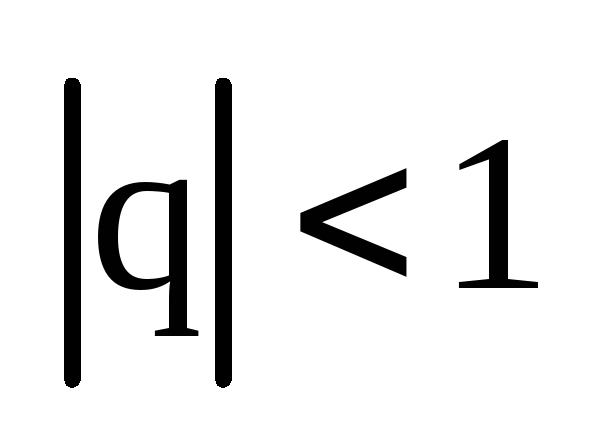и расходящимся, если.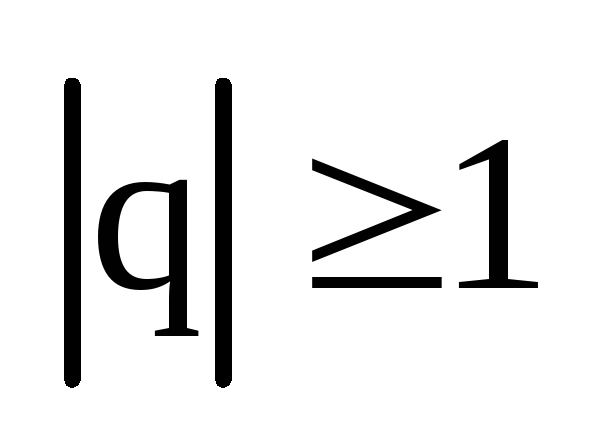

Также
встречается гармонический
ряд
(ряд
).
Этот рядрасходящийся

Из огромного многообразия всевозможных множеств
особый интерес представляют так называемые числовые множества
, то есть, множества, элементами которых являются числа. Понятно, что для комфортной работы с ними нужно уметь их записывать. С обозначений и принципов записи числовых множеств мы и начнем эту статью. А дальше рассмотрим, как числовые множества изображаются на координатной прямой.

Навигация по странице.

Поздний палеолит

Данный период ознаменовался появлением кроманьонца – древнего человека, который внешне имел много общего с современным человеком. У него был высокий лоб, хорошо выраженный подбородок, развитая мелкая моторика рук.

К основным достижениям позднего палеолита относят:

изготовление примитивных лодок;
плетение корзин из ивовых прутьев;
изготовление костяных игл, с помощью которых сшивали одежду;
активное развитие искусства: наскальная живопись, изготовление примитивных фигурок из костей и бивней мамонта;
одомашнивание диких животных, первой из которых стала собака;
определение времени по лунному и солнечному календарям;
замена первобытного общества на родовую общину;
изготовление глиняной посуды.

Рис. 3. Наскальная живопись.

На территории России стоянки первобытных людей эпохи палеолита были найдены в населенных пунктах Сунгирь, Костенки, Карачарово, и некоторых других. Ценные археологические находки помогли ученым восстановить образ жизни, особенности ведения хозяйства далеких предков.

Первобытная история берет свое начало в каменном веке, на смену которому пришел бронзовый, а затем – железный век. Данные этапы развития человечества имели большое значение, поскольку предопределили формирование современного общества.

Средний палеолит

На протяжении всего среднего палеолита происходило постепенное развитие и усовершенствование способностей человека прямоходящего. В ходе эволюции появился новый вид – неандерталец, чей объем мозга был уже гораздо ближе современному человеку. Также он отличался массивным телосложением и высоким ростом.

Рис. 2. Неандерталец.

Средний палеолит – это эпоха выживания, поскольку жизнь первобытных людей протекала на фоне крайне суровых климатических условий, в ледниковый период.

Для эпохи среднего палеолита характерны следующие черты:

самостоятельное добывание огня путем его высекания;
появление новых видов орудий: ножей, копий, наконечников для стрел, скребков;
совершенствование социальной организации – люди объединяются в большие группы, заботятся о стариках;
зарождение первобытного искусства – появление самых первых наскальных рисунков.

Определение и основные понятия

Комплексные числа — это числа вида a + bi, где a и b — действительные числа, а символ i — мнимая единица.

Действительная часть комплексного числа a + bi обозначается Re(z) и равна a.

Мнимая часть комплексного числа a + bi обозначается Im(z) и равна b.

Комплексным сопряжением комплексного числа a + bi называется число a — bi и обозначается z̄.

Модулем комплексного числа a + bi называется неотрицательное число |z| и равно корню из суммы квадратов действительной и мнимой частей числа.

Аргументом комплексного числа a + bi называется угол φ между положительным направлением оси вещественных чисел и отрезком, соединяющим начало координат и точку, соответствующую числу a + bi в комплексной плоскости.

Операции над комплексными числами аналогичны операциям над действительными числами и включают сложение, вычитание, умножение, деление, а также сравнение и возведение в степень.

Власть и социальные нормы в первобытном обществе[]

Основная статья: Власть и социальные нормы в первобытном обществе

Первые формы институтов власти и первые общеобязательные нормы поведения сформировались уже на первобытной стадии развития общества. Для этого периода характерно отсутствие политической власти и государственных институтов. Социальные нормы в этот период носят характер обычаев, традиций, обрядов и табу. В науке вопрос о том, можно ли считать данные социальные нормы правом или протоправом, является дискуссионным.

Надо признать, что данные утверждения действительно являются весьма спорными и дискуссионными, поскольку из них следует, что власть сформировалась «при первобытнообщинном строе» при отсутствии власти(?), в связи с чем представители классической исторической науки продолжают придерживаться классического представления о возникновении власти в период распада первобытнообщинного строя, того самого вида общественного устройства, которое древние греки, первые теоретики возникновения власти и государства, на примере окружающих их «диких» племен называли «анархией» в противовес цивилизованным видам управления обществом в Древней Греции как видов рабовладельческого государства — «монархии», «олигархии», «деспотии», «аристократии», «поликратии», «тирании», «плутократии», «демократии».

Извлечение корня.

Рассмотрим уравнение
$$
z^n=a,\label{ref22}
$$
где $a\neq 0$ — комплексное число, $n$ — натуральное число.

Если $z=re^{i\varphi}, \ a=\rho e^{i\theta}$, то уравнение \eqref{ref22} примет вид
$$
r^n e^{in\varphi}=\rho e^{i\theta},\nonumber
$$
откуда
$$
r^n=\rho,\quad n\varphi=\theta+2k\pi,\quad k\in\mathbb{Z},\nonumber
$$
и поэтому
$$
r=\sqrt{\rho},\qquad \varphi_k=\frac{1}{n}(\theta+2k\pi),\quad k\in \mathbb{Z},\label{ref23}
$$
то есть числа
$$
z_k=\sqrt{\rho}e^{i\varphi_k}\label{ref24}
$$
являются корнями уравнения \eqref{ref22} и других корней это уравнение не имеет.

Заметим, что числа $z_0,\ z_1,\ …,\ z_{n-1}$ различны, так как их аргументы $\displaystyle\varphi_0=\frac{\theta}{n},\ \varphi_1=\frac{\theta}{n}+\frac{2\pi}{n},\ …,\ \varphi_{n-1}=\frac{\theta}{n}+\frac{2\pi(n-1)}{n}$ различны и отличаются друг от друга меньше, чем на $2\pi$. Далее, $z_n = z_0$, так как $|z_n| = |z_0|=\displaystyle\sqrt{\rho}$ и $\varphi_n=\varphi_0+2\pi$. Аналогично, $z_{n+1} = z_1,\ z_{-1} = z_{n-1}$ и т. д.

Итак, при $a\neq 0$ уравнение \eqref{ref22} имеет ровно $n$ различных корней, определяемых формулами \eqref{ref23} и \eqref{ref24}, где $k=0,1,…,n-1$.

На комплексной плоскости точки $z_k\ (k=\overline{0,n-1})$ располагаются в вершинах правильного $n$-угольника, вписанного в окружность радиуса $\displaystyle \sqrt{\rho}$ с центром в точке 0.

Пример 5.

Найти все корни уравнения $z^4 = 1 + i$.

$\triangle$ Корни $z_k\ (k = \overline{0,3})$ этого уравнения определяются формулами \eqref{ref23} и \eqref{ref24}, где $\displaystyle \rho=|1 + i| =\sqrt{2},\ \theta=\frac{\pi}{4}$, то есть
$$
z_k=\sqrt{2}e^{i\varphi_k},\nonumber
$$
где
$$
\varphi_k=\frac{\pi}{16}+\frac{\pi k}{2},\quad k=0,1,2,3.\nonumber
$$

Рис. 31.6

Точки $z_k$ располагаются в вершинах квадрата (рис. 31.6). $\blacktriangle$

Ссылки[]

Barnard, Alan. From Mesolithic to Neolithic Mode of Thought // Whittle, A. and Cummings, V. (ed.) Going Over. The Mesolithic-Neolithic Transition in North-West Europe. Proceedings of the British Academy 144, 2007. P. 5-19.
Адамович Т. И. Экономическая история (недоступная ссылка с 23-05-2013 (3795 дней)) Минск: БГУ, 2004. — 75 c. ISBN 985-485-179-6 Ориентация через периодизацию экономической истории
Щукин М. Б. На рубеже эр. Спб. 1994
Ю.Семенов «Социальная организация отношений между полами: Возникновение и развитие»
Г. Б. Поляк «История мировой экономики»
Мартин Ауэр. «Откуда берётся война? Конфликт, кооперация и конкуренция с точки зрения самоорганизации систем»
Юрий Семёнов «Возникновение религии и её первая, исходная форма — магия»

Семёнов, Юрий Иванович:

«Переход от первобытного общества к классовому: пути и варианты развития». Часть I Часть II
Формы общественной воли в доклассовом обществе: табуитет, мораль и обычное право
Тотемизм, первобытная мифология и первобытная религия
О методике реконструкции развития первобытного общества по данным этнографии
Введение во всемирную историю. Выпуск 2. История первобытного общества

Ефименко П. П. Первобытное общество. Очерки по истории палеолитического времени (недоступная ссылка с 23-05-2013 (3795 дней) — история, копия)
Лекция «История первобытного общества»
Периодизация первобытной истории
Статья «Первобытнообщинный строй» в БСЭ
Всемирная история. Энциклопедия. Том 1. (1956 год)
Таблица «Начальная история (до 3000 г. до н. э.)» на сайте «Хронос»
Первобытная культура

Википедия Первобытное общество адрес
Викисловарь — адрес
Викицитатник — адрес
Викиучебник — адрес
Викитека — адрес
Викиновости — адрес
Викиверситет — адрес
Викигид — адрес

Выделить Первобытное общество и найти в:

Вокруг света общество адрес
Академик общество/ru/ru/ адрес
Астронет адрес
Элементы общество+&search адрес
Научная Россия общество&mode=2&sort=2 адрес
Кругосвет общество&results_per_page=10 адрес
Научная Сеть
Традиция — адрес
Циклопедия — адрес
Викизнание — общество адрес

Bing
Yahoo
Яндекс
Mail.ru
Рамблер
Нигма.РФ
Спутник
Google Scholar
Апорт
Архив Интернета
Научно-популярные фильмы на Яндексе
Документальные фильмы

Список ru-вики
Вики-сайты на русском языке
Список крупных русскоязычных википроектов
Каталог wiki-сайтов
Русскоязычные wiki-проекты
Викизнание:Каталог wiki-сайтов
Научно-популярные сайты в Интернете
Лучшие научные сайты на нашем портале
Лучшие научно-популярные сайты
Каталог научно-познавательных сайтов
НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов

Страница — краткая статья
Страница 1 — энциклопедическая статья
Разное — на страницах: 2 , 3 , 4 , 5
Прошу вносить вашу информацию в «Первобытное общество 1», чтобы сохранить ее

Характерные черты палеолита

История происхождения человека характеризуется большой временной протяженностью. Благодаря археологическим раскопкам ученым удалось установить основные этапы эволюции человека, важнейшие изобретения и проблемы, которые были характерны для каждого периода.

Палеолит представляет собой важный исторический период, во время которого происходило становление человека, формирование первобытного общества.

В эпоху палеолита природно-климатические условия, животный и растительный мир существенно отличались от современных. Люди жили небольшими сообществами, используя для своих бытовых нужды каменные орудия. В тот период они еще не могли шлифовать камень и использовать другие твердые породы, однако научились применять в своих целях дерево, кожу, кости.

Рис. 1. Каменные орудия труда.

Для всей эпохи характерно присваивающее хозяйство: первобытные люди обеспечивали себе пропитание за счет собирательства и охоты. Скотоводство и земледелие еще не были известны, а рыболовство только начинало развиваться. Важнейшим достижением человека в эпоху палеолита стало появление речи.

ТОП-4 статьи

которые читают вместе с этой

Палеолит – самый продолжительный этап каменного века, который для большего удобства был разделен учеными на три основные эпохи:

нижний (ранний) палеолит;
средний палеолит;
верхний (поздний) палеолит.

Все эпохи палеолита существенно различаются между собой по способам изготовления орудий труда и оружия, их формам, по антропологическим характеристикам.