Diagonalize matrix calculator

Приведение квадратной матрицы к диагональному виду. Критерии приводимости квадратной матрицы к диагональному виду

Фрагмент текста работы

§ 2. Приведение квадратной матрицы к диагональному виду

Говорят, что квадратная матрица А с элементами из поля P приводится к диагональному виду над P, если существует невырожденная квадратная матрица Т с элементами из P такая, что матрица – диагональная.

Критерии приводимости квадратной матрицы к диагональному виду. 1. Если А – квадратная матрица -го порядка с элементами из поля P, – линейное пространство над Р, – тот линейный оператор, матрица которого в некотором базисе пространства совпадает с А, то для приводимости матрицы А к диагональному виду над полем Р необходимо и достаточно, чтобы в существовал базис, состоящий из собственных векторов оператора f.

2. Для того чтобы квадратная матрица А n-го порядка приводилась к диагональному виду над полем Р необходимо и достаточно, чтобы все корни ее характеристического уравнения принадлежали этому полю и для каждого из них выполнялось условие

, (7)

где – кратность корня характеристического уравнения матрицы А.

При решении задач первый критерий, пожалуй, проще в применении, хотя студенты обычно предпочитают второй.

В том случае, когда все характеристические числа матрицы А различны и принадлежат полю Р, эта матрица приводится к диагональному виду над Р. Если матрица А приводится к диагональному виду – матрице , то диагональными элементами последней являются собственные значения матрицы А, а матрица Т, приводящая А к диагональному виду, есть не что иное, как матрица перехода от исходного базиса к базису из собственных векторов.

Из всего вышесказанного вытекает, что для приведения квадратной матрицы к диагональному виду над полем Р следует:

1) составить характеристический многочлен матрицы А и найти его корни. Если какой-либо из них не принадлежит полю Р, то А к диагональному виду не приводится;

2) если все корни характеристического уравнения принадлежат полю Р, то для кратных корней проверить условие (7) (для однократных оно выполняется всегда). Если для какого-то из корней (7) не выполняется, то А к диагональному виду не приводится;

3) если для каждого из собственных значений условие (7) выполняется, то А к диагональному виду приводится. Записываем этот диагональный вид – матрицу , располагая на ее главной диагонали собственные значения в произвольном порядке, причем каждое из значений повторяется столько раз, какова его кратность;

4) для каждого из найденных собственных значений находим собственные векторы и составляем из них базис;

5) записываем матрицу Т, приводящую А к диагональному виду, – матрицу перехода от исходного базиса к базису из собственных векторов, сохраняя порядок, установленный матрицей .

Пример 1. Найти диагональный вид матрицы А над полем действительных чисел и невырожденную матрицу Т, приводящую к этому диагональному виду, если

►Проводим решение по намеченному плану.

+

2.Все корни действительны и однократны, поэтому матрица А приводится к диагональному виду.

3. .

4. Все собственные векторы можно найти с помощью алгебраических дополнений. Кроме того, вспомним, что, если мы нашли один собственный вектор, то любой вектор, ему коллинеарный, также является собственным с тем же самым собственным значением.

: ; ,

(алгебраические дополнения к элементам первой строки);

: ; =

(алгебраические дополнения к элементам второй строки);

: ; ,

(алгебраические дополнения к элементам первой строки).

5. Составляем матрицу перехода от исходного базиса к, построенному базису , записывая в столбцы матрицы координатные столбцы векторов , и соответственно:

.◄

Пример 2. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.

►Составляем и решаем характеристическое уравнение:

Матрица имеет только одно собственное значение , но его кратность равна трем. Проверяем выполнение условия (4.58):

Условие не выполняется, значит, матрица к диагональному виду не приводится.◄

Пример 3. Проверить, приводится ли матрица А к диагональному виду. Если приводится, найти этот диагональный вид и невырожденную матрицу Т, приводящую нему.

► Решение опять проводим по намеченному плану.

–

2. Проверяем выполнение условия (7) для кратного корня:

. (8)

Таким образом, , условие выполняется, матрица к диагональному виду приводится.

3. .

4. Так как , то , т. е для первого собственного значения можно найти два линейно независимых собственных вектора. По одной из строк матрицы (8), разделив все ее элементы на общий множитель, выписываем единственное уравнение для отыскания координат собственных векторов и решаем его: , . В качестве двух линейно независимых решений можно взять, например

Критерий диагонализируемости

Определение. Оператор $A$ – диагонализируемый, если существует базис $(e_i)$, в котором матрица оператора имеет диагональный вид.

$A=
\begin{pmatrix}
\lambda_1 & & 0 \\
& \ddots & \\
0 & & \lambda_n
\end{pmatrix}$

Определение. Спектр оператора $A$ – множество собственных значений оператора $A$. Обозначение: $\Spec A$ или $\Sp(A)$. Собственные значения учитываются с геометрическими кратностями.

Точка спектра – простая, если ее кратность равна 1.

Спектр – простой, если все точки – простые.

Пример. Над $\mathbb{R}$ спектр может быть пустым множеством, например поворот на угол $\alpha$:

$A=
\begin{pmatrix}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{pmatrix}$

Лемма. Собственные векторы, принадлежащие различным собственным значениям, линейно независимы.

$\sum\limits_{\lambda \in \Spec A} V^{\lambda}$ – прямая, где $V^{\lambda}=\{ v ~|~ Av=\lambda v \}$

Вообще говоря, $\sum V^{\lambda} \neq V$.

$\blacktriangle$ Пусть $\lambda_1,…,\lambda_m$ – собственные значения (различные).
$V^{\lambda_1},…,V^{\lambda_m}$ – соответствующие собственные подпространства.

Выберем в каждом $V^{\lambda_i}$ по одному вектору $e_i$. Докажем, что $\{ e_i \}_{i=1}^m$ – линейно независимы.

Индукция по $m$. $m=1$ – очевидно.

Шаг индукции. Предположим, что существует нетривиальная линейная комбинация $\alpha_1e_1+…+\alpha_me_m=0$, где для определенности $\alpha_1 \neq 0$.

Применим оператор $A,~Ae_i=\lambda_i e_i$

$\alpha_1\lambda_1e_1+…+\alpha_m\lambda_me_m=0$

$\alpha_1(\lambda_1-\lambda_m)e_1+…+\alpha_{m-1}(\lambda_{m-1}-\lambda_m)e_{m-1}=0$

По предположению индукции $\alpha_i(\lambda_m — \lambda_i)=0,~i=1,…,m-1$, но

$\alpha_1 \neq 0,~\lambda_1 \neq \lambda_m \Rightarrow \alpha_1(\lambda_m — \lambda_1) \neq 0$, противоречие, поэтому не существует нетривиальной линейной комбинации $\Rightarrow e_1,…e_{m-1}$ – линейно независимы. $\blacksquare$

Теорема (критерий диагонализируемости). Пусть $A$ – линейный оператор в конечномерном векторном пространстве над полем $\mathbb{F}$. Для диагонализируемости $A$ необходимо и достаточно:

1) все корни $\chi_A(\lambda)$ лежат в $\mathbb{F}$

2) геометрическая кратность любого собственного значения равна алгебраической кратности.

$\blacktriangle$ Докажем, что 1), 2) $\Rightarrow$ диагонализируемость.

Пусть $\lambda_1,…,\lambda_m$ – собственные значения. $V^{\lambda_i}$ – соответствующие собственные подпространства.

$\dim V^{\lambda_i}=k_i,~\sum\limits_{i=1}^m k_i=n$

$\sum V^{\lambda_i}$ – прямая, $V^{\lambda_1} \oplus … \oplus V^{\lambda_m}=V$, т.к $\sum \dim V^{\lambda_i}=\dim V$

Выбирая базисы в $V^{\lambda_i}$ и объединяя их, получим базис в $V \Rightarrow$ в этом базисе матрица $A$ – диагональная.

Докажем теперь, что диагонализируемость $\Rightarrow$ 1), 2).

Пусть $\lambda_1,…\lambda_m$ – собственные значения $A$.

$l_i=\dim V^{\lambda_i},~\sum V^{\lambda_i}$ – прямая.

Т.к. оператор $A$ диагонализируем $\Rightarrow V^{\lambda_1},…,V^{\lambda_m}$ порождают $V \Rightarrow V=V^{\lambda_1} \oplus … \oplus V^{\lambda_m} \Rightarrow$ в базисе, получающемся объединением базисов в $V^{\lambda_i}$, $A$ записывается:

$A=
\begin{pmatrix}
\lambda_1 & & & & & & & & & & \\
& \ddots & & & & & & & & & \\
& & \lambda_1 & & & & &\Huge 0 & & & \\
& & & \lambda_2 & & & & & & & \\
& & & & \ddots & & & & & & \\
& & & & & \lambda_2 & & & & & \\
& & & & & & \ddots & & & \\
& &\Huge 0 & & & & & \lambda_m & & \\
& & & & & & & & \ddots & \\
& & & & & & & & & \lambda_m \\
\end{pmatrix}$

$\chi_A(\lambda)=(\lambda — \lambda_1)^{l_1}…(\lambda — \lambda_m)^{l_m},~\lambda_1,…,\lambda_m \in \mathbb{F} \Rightarrow l_i$ – в точности алгебраические кратности $\lambda_i. ~\blacksquare$

6.6. Квадратичные формы

Опр. Квадратичной формой называется выражение вида:

Пример:

Запишем матрицу этой квадратичной формы

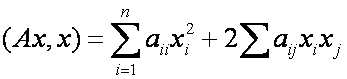
Опр. Квадратичная форма называется
положительно определенной, если для любого х квадратичная форма положительна.
Квадратичная форма называется отрицательно определенной, если для любого х
квадратичная форма отрицательна.

Квадратичная форма называется знакопеременной,
если для одних элементов х она положительна, а для других элементов у она
отрицательна.

Критерий Сильвестра. Квадратичная
форма будет положительно определенной, если все угловые миноры матрицы А
положительны, т.е. если

Квадратичная форма называется
отрицательно определенной, если знаки угловых миноров матрицы А чередуются,
причем

Матрица А в базисе, составленном из
собственных векторов имеет диагональный вид. , причем диагональными элементами являются собственные
элементы этой матрицы. Это значит, что если матрицу квадратичной формы привести
к диагональному виду, то квадратичная форма такой матрицы примет простой вид: , (1), т.е. будет содержать квадраты элементов

Выражение (1) называется каноническим
видом квадратичной формы.

6.1 Понятие линейного оператора

О
п р е д е л е н и е. Всякое
правило, с помощью которого элементу х
линейного пространства V ставится в соответствие некоторый элемент у линейного пространства W, называется оператороми обозначается А. Итак,

y=Ах=А(х)

О
п р е д е л е н и е. Оператор А называется линейным, если он
удовлетворяет требованиям:

I.
А(х+у)=Ах+Ау,

II. .

В случае n=1 (одномерное пространство) линейный оператор – это
обычная линейная функция y=kx+b.

Нулевой оператор – это оператор 0(х)=0.

Единичный оператор I(х)=x не
изменяет элемента.

Противоположный
оператор – это оператор(–A).

О п р е д е л е н и е. Суммой операторов А
и В называется оператор A+B,
действующий по правилу (А+В)х=Ах+Вх.

Произведение операторов: (АВ)х=А(Вх).

Обратный оператор –это оператор, произведение которого с
исходным дает единичный оператор.

1.2. Простейшие операции с матрицами

Матрицы можно умножать на числа. При этом каждый элемент умножается на это
число. Например —

Рис. 3 Умножение
матрицы на число

Две матрицы одинаковой размерности можно поэлементно
складывать и вычитать.
Например,

Рис. 4
Сложение матриц

В результате умножения на число и сложения получается матрица той же
размерности.

Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается
O. Очевидно, что A+O =
A, A−A = O и
0A = O.

Матрицу можно транспонировать. При этой операции матрица
переворачивается, т.е. строки и столбцы меняются местами. Транспонирование
обозначается штрихом, A’ или индексом
At. Таким образом, если A =
{a_ij, i = 1,…, I; j =
1,…,J}, то At = {a_ji,
j = 1,…,J; i = 1,…, I}. Например

Рис.
5 Транспонирование матрицы

Очевидно, что (At)t =
A, (A+B)t
= At+Bt.

2.17. Проекция на подпространство

Рассмотрим подпространство RK, натянутое на векторы
X = (x₁,
x₂,…,x_K) в
пространстве RN. Матрица базиса X имеет
размерность (N×K). Любой вектор y из
RN может быть спроецирован на подпространство
RK, т.е. представлен в виде  

y =
y|| + y⊥, 

где вектор
y|| принадлежит RK, а вектор
y⊥ ортогонален y||. 

Рис.
26 Проекция на подпространство

Проекцию y|| можно
представить как результат действия
проекционной матрицы P

y||
= Py

Проекционная матрица определяется как

Пример.

Рис.
27 Проекционное разложение

Заключение

Матричные методы активно используются при анализе данных, в том
числе и хемометрическими методами. 

Примеры приведены в пособиях

• Матричные операции в Excel и в
  сопровождающем его файле Excel.xls   

• Метод главных
  компонент (PCA) и в
  сопровождающем его файле People.xls  

• Калибровка и в
  сопровождающем его файле Calibration.xls

• Классификация и в
  сопровождающем его файле
  Iris.xls

• Разрешение многомерных кривых и в
  сопровождающем его файле MCR.xls.

оглавление  
ДМ  
экономическая информатика  
визуальные среды — 4GL  
Теория и практика обработки информации

Знаете ли Вы, что объективно обусловленная оценка ресурса (продукции) — это величина прироста экономического эффекта, обусловленного малым изменением доступного объёма ресурса или величины планового задания по выпуску продукции. При использовании экономико-математического моделирования численно равна двойственной оценке соответствующего ограничения. Измеряется в единицах измерения экономического эффекта в расчёте на единицу ресурса (продукции).

НОВОСТИ ФОРУМАРыцари теории эфира

10.11.2021 — 12:37: ПЕРСОНАЛИИ — Personalias -> — Карим_Хайдаров.10.11.2021 — 12:36: СОВЕСТЬ — Conscience -> — Карим_Хайдаров.10.11.2021 — 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.10.11.2021 — 12:35: ЭКОЛОГИЯ — Ecology -> — Карим_Хайдаров.10.11.2021 — 12:34: ВОЙНА, ПОЛИТИКА И НАУКА — War, Politics and Science -> — Карим_Хайдаров.10.11.2021 — 12:34: ВОЙНА, ПОЛИТИКА И НАУКА — War, Politics and Science -> — Карим_Хайдаров.10.11.2021 — 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.10.11.2021 — 09:18: НОВЫЕ ТЕХНОЛОГИИ — New Technologies -> — Карим_Хайдаров.10.11.2021 — 09:18: ЭКОЛОГИЯ — Ecology -> — Карим_Хайдаров.10.11.2021 — 09:16: ЭКОЛОГИЯ — Ecology -> — Карим_Хайдаров.10.11.2021 — 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.10.11.2021 — 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.

3.7. Диагонализация матрицы линейного оператора

Пусть линейный оператор . Рассмотрим в произвольный базис . Пусть в этом базисе линейному оператору соответствует матрица . Существует ли такой базис в пространстве , в котором матрица линейного оператора была бы диагональной?

Очевидно, если такой базис существует, то по Свойству 1 (п. 3.6) диагонализация матрицы произойдет в результате преобразование подобия.

Имеет место следующая

Теорема. Если в существует базис из собственных векторов линейного оператора то матрица линейного оператора будет диагональной в этом базисе.

Выясним, при каких условиях существует базис из собственных векторов линейного оператора.

Пусть – собственные значения линейного оператора кратностей , причём . Если для каждого существует собственных векторов – решений ФСР соответствующей однородной СЛАУ, то существует базис из собственных векторов, а значит, матрицу линейного оператора можно привести к диагональному виду. В частности, если , т. е. спектр линейного оператора простой, то базис из собственных векторов существует. Однако, если среди корней характеристического уравнения найдётся хотя бы одна пара комплексно-сопряжённых, то в вещественном линейном пространстве не существует базиса из собственных векторов.

Покажем, например, что, если спектр простой, то матрица линейного оператора в базисе из собственных векторов будет диагональной.

Рассмотрим квадратную матрицу , в столбцах которой стоят координаты собственных векторов , соответствующих собственным значениям . Это означает, что матрица является матрицей перехода к базису из собственных векторов. Очевидно, в этом случае , т. е. матрица – невырожденная, и для неё существует обратная – Из определения собственных векторов линейного оператора следует, что

(16)

Где – векторы-столбцы, соответствующие собственным векторам линейного оператора . Равенство (16) можно записать в более компактной форме:

(17)

Где – диагональная матрица, у которой на главной диагонали расположены собственные числа т. е.

Умножим обе части равенства (17) слева на матрицу :

или (18)

Это означает, что матрица линейного оператора при переходе к базису из собственных векторов станет диагональной в результате преобразования подобия (18).

Пример 14. Найти собственные значения и собственные векторы линейного оператора , заданного в некотором базисе матрицей . Построить, если это возможно, базис из собственных векторов линейного оператора и найти матрицу линейного оператора в этом базисе. Выполнить проверку.

Решение. Составим характеристическое уравнение:

Найдём собственные векторы линейного оператора:

;

Т. е.

Собственные значения линейного оператора различны, значит, собственные векторы линейно независимы, т. е. образуют базис. В этом базисе матрица линейного оператора будет диагональной:

.

Матрица перехода к базису из собственных векторов .

Проверим правильность проведенных вычислений. По формуле (7) Найдём :

.

Ответ: .

Пример 15. Линейный оператор в некотором базисе задан матрицей Существует ли базис из собственных векторов линейного оператора ?

Решение. Составим характеристическое уравнение:

Собственные значения линейного оператора Найдём соответствующие им собственные векторы: Т. е. . Все остальные собственные векторы имеют вид . Это означает, что базис из собственных векторов не существует.

Пример 16. Найти собственные векторы и собственные значения линейного оператора , заданного в некотором базисе матрицей . Можно ли привести матрицу к диагональному виду?

Решение. Составим характеристическое уравнение:

Т. е.

Или

Собственные значения линейного оператора Найдём собственные векторы:

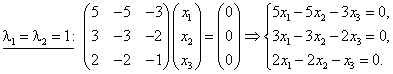
Эта система эквивалентна следующей:

Т. е. ФСР этой системы состоит из одного решения, например, Собственным значениям и соответствует собственный вектор . Другие собственные векторы, соответствующие собственным значениям и , могут быть получены из умножением на произвольное вещественное число. Например, .

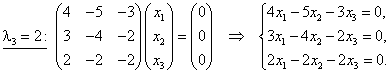
Так как 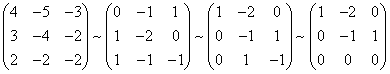, то значит,

линейно зависимы, значит, совокупность собственных векторов также линейно зависима, т. е. собственные векторы линейного оператора не образуют базис в . Поэтому матрица не может быть приведена к диагональному виду.

What Is the Definition of a Diagonal Matrix and What Are Its Properties?

A diagonal matrix is a special type of square matrix where all the entries outside the main diagonal are zero, and the entries on the main diagonal can be zero or any other number. The main diagonal of a matrix consists of elements from the top left to the bottom right (i.e., elements where the row number equals the column number).

In mathematical terms, the matrix A=\left is diagonal if a_{ij}=0 when i\ne j.

An example of a diagonal matrix is D=\left.

Properties of a Diagonal Matrix:

• Addition and Subtraction: When adding or subtracting two diagonal matrices, the operation is performed element-wise on the diagonal elements.
• Scalar Multiplication: When a diagonal matrix is multiplied by a scalar, each diagonal element of the matrix is multiplied by this scalar.
• Matrix Multiplication: The product of two diagonal matrices is also a diagonal matrix. Each diagonal element is the product of corresponding diagonal elements in the multiplied matrices.
• Identity Matrix: A special type of diagonal matrix, called the identity matrix, plays a similar role to the number 1 in real number multiplication. The identity matrix has ones on the diagonal and zeros elsewhere.
• Matrix Inverse: A diagonal matrix is invertible if all its diagonal elements are non-zero. The inverse of a diagonal matrix is a diagonal matrix with reciprocal elements on the diagonal.
• Power of a Matrix: The power of a diagonal matrix (where the power is a positive integer) is a diagonal matrix, with each element being the corresponding power of the original matrix’s elements.
• Eigenvalues and Eigenvectors: The eigenvalues of a diagonal matrix are its diagonal elements, and the corresponding eigenvectors are the columns of the identity matrix.
• Determinant: The determinant of a diagonal matrix is the product of its diagonal elements.

The Diagonalize Matrix Calculator can help you in diagonalizing a given square matrix.

5.4. Евклидово пространство

О п р е д е л е н и. Евклидовым пространством называется линейное
пространство, удовлетворяющее двум требованиям:

1.Существует правило, с помощью которого любым двум элементам
линейного пространства хиу ставится в соответствиевещественное число, называемое скалярным
произведением этих элементов и обозначаемое символом(х,у).

2.Скалярное произведение удовлетворяет следующим
аксиомам

I.,

II.,

III.(x,y)= (x,y)

IV.(x,x) 0, (x,x)=0 только
для нулевого элемента.

П р и м е р 1. Множество геометрических векторов с обычным скалярным произведением.

П р и м е р 2. Множество функций непрерывных на отрезке со скалярным
произведением в виде интеграла

,

где – функции, непрерывные
на отрезке [a,b

П р и м е р 3. Множество всевозможных наборов из n чисел, т.е. арифметическое линейное пространство со
скалярным произведением, определяемым выражением

П р и м е р 4. Множество элементов арифметического пространства со скалярным
произведением, определяемым выражениями

,

где– элементы матрицы

.

При евклидово пространство
совпадает с обычным геометрическим пространством, при– не имеет смысла.

Рассмотрим основные свойства произвольного евклидова
пространства.

Т е о р е м
а. Любые два элементахиуудовлетворяют неравенству

.(1)

Д о к а з а т е л ь с т в о. Построим вектор и найдем. Тогда в силу
аксиомы IV скалярного произведения будет справедливо неравенство

,

Которое с помощью
аксиомI – III
преобразовать следующим образом

.(2)

Левая часть неравенства (2) квадратный трёхчлен
относительно . Необходимым и достаточным условием неотрицательности
последнего является условие

,

откуда следует

,

что совпадает с выражением (1). Выражение (1) принято
называть неравенством Коши-Буняковского.

О п р е д е л е н и е.. Линейное пространство называется нормированным, если
оно удовлетворяет двум требованиям:

1) Существует правило, с помощью которого каждому
элементу х этого пространства
ставится в соответствие вещественное число, называемое нормой или длиной этого
элемента и символически обозначается .

2) При этом выполняется три аксиомы:

I. и =0 только при .

II.

III. .

Последнее условие называется неравенством треугольника
(или неравенством Минковского).

В случае трехмерного пространства

.

В качестве примера можно взять евклидово пространство с
нормой .

Углом между векторами х и у
называетсятот угол, косинус которого
определяется с помощью равенства

.

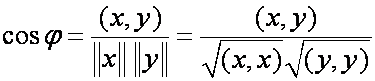Отличие скалярного произведения геометрических векторов
от скалярного произведения евклидова пространства заключается в том, что в
евклидовом пространстве скалярное произведение вводится аксиоматически и
свойства скалярного произведения не доказываются, тогда какдля геометрических векторов вводится понятие
угла и длины, которые можно измерить и свойства доказать.

О п р е д е л е н и е. Векторы х
и у евклидова пространства называются
ортогональными, если (х,у)=0,
т.е..Но измерить этот
угол невозможно.

О п р е д е л е н и е. Базис называется
ортонормированным базисом, если векторы попарно ортогональны и
по длине равны единице, т.е.

Любую систему изnлинейно
независимых векторов , как известно, можно считать базисом n-мерного
линейного пространства. Оказывается, что эти векторы можно преобразовать таким
образом, чтобы в результате получился ортонормированный базис. Преобразование
осуществляется по схеме:

,,

,,

,,

,.

,

,

так как

.

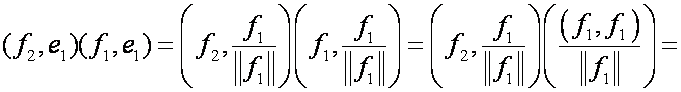
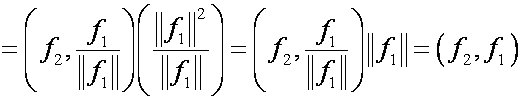Рассмотренный
процесс преобразования произвольного базиса в ортонормированный базис
называется процессом ортогонализации или схемойГрама-Шмидта.

Очевидно,
скалярное произведение в ортонормированном базисе будет определяться выражением
(х,у)= т.е скалярное произведение равно сумме произведений
одноименных координат.

Анализ эффективности и преимущества преобразования матрицы к диагональному виду

Преобразование матрицы к диагональному виду имеет ряд преимуществ и может быть полезным во многих областях математики и науки. Рассмотрим анализ эффективности и основные преимущества данного преобразования.

1. Упрощение алгоритмов и вычислений

Когда матрица приводится к диагональному виду, множество операций над ней становятся значительно проще. Например, вычисление определителя матрицы, нахождение собственных значений и векторов, решение систем линейных уравнений и многие другие задачи сводятся к элементарным операциям с диагональными матрицами.

Это позволяет упростить алгоритмы и методы решения различных математических задач. Кроме того, диагональные матрицы обладают особыми свойствами, такими как коммутативность и ассоциативность операций. Это упрощает проведение численных вычислений и улучшает их эффективность.

2. Выделение главных компонент

Еще одним преимуществом преобразования матрицы к диагональному виду является возможность выделения главных компонент данных. Путем диагонализации матрицы и выбора наибольших по модулю собственных значений, можно определить основные факторы, влияющие на данные.

Это пригодно, например, в анализе данных, машинном обучении и распознавании образов. Выделение главных компонент позволяет сократить размерность данных, улучшить их интерпретируемость и снизить размерность входного пространства. Это в свою очередь упрощает процесс обработки данных и позволяет получить более надежные результаты.

3. Разделение независимых переменных

Преобразование матрицы к диагональному виду может также использоваться для разделения независимых переменных в множественном регрессионном анализе. Диагональные матрицы являются диагональными матрицами, являются диагонализованными и позволяют найти независимые компоненты данных.

Это полезно, например, в исследовании взаимосвязей переменных, идентификации влияющих факторов и построении моделей прогнозирования. Разделение независимых переменных позволяет более точно определить и оценить их влияние на зависимую переменную и улучшить качество модели.

4. Оптимизация вычислительных процессов

Приведение матрицы к диагональному виду также может быть полезным с точки зрения оптимизации вычислительных процессов. Диагональные матрицы обладают свойством, что произведение любой двух диагональных матриц также является диагональной матрицей.

Это позволяет существенно сократить количество операций при умножении матриц и ускоряет выполнение алгоритмов, основанных на матричных операциях. Такая оптимизация вычислительных процессов может быть важна в больших вычислительных задачах, где производительность является критическим фактором.

5. Упрощение структуры данных

Когда матрица приводится к диагональному виду, структура данных становится более простой и интуитивно понятной. Каждый элемент диагональной матрицы содержит информацию только о самом элементе, а не о взаимосвязи с другими элементами.

Это полезно в различных задачах, таких как анализ данных, паттерн-распознавание, графическое представление и моделирование. Простая структура данных упрощает их хранение, визуализацию и использование в более сложных алгоритмах и системах.

Заключение

Преобразование матрицы к диагональному виду является полезным и мощным инструментом в математике и науке. Оно позволяет упростить алгоритмы и вычисления, выделить главные компоненты данных, разделить независимые переменные, оптимизировать вычислительные процессы и упростить структуру данных.

Это открывает широкие возможности для применения преобразования матрицы к диагональному виду в различных областях знаний и научных исследований.