Дирекционный угол в треугольнике

Способы изображения земной поверхности. Метод проекций в геодезии

_______На местности точки, линии, углы и контуры расположены в силу неровностей земной поверхности на возвышениях или впадинах. Так как возвышения и впадины являются пространственными формами, изобразить их на бумаге в виде плоской карты или плана достаточно непросто. Способы изображения земной поверхности на плоскости основываются на методе проекций.

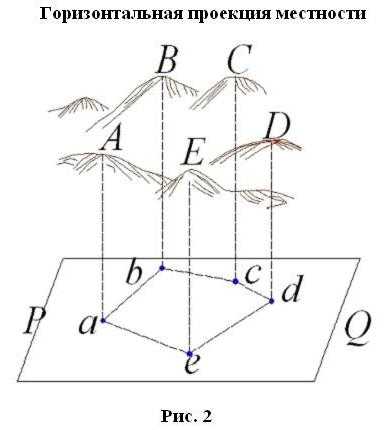
_______При изучении действительной поверхности Земли точки местности проецируют отвесными линиями на поверхность земного эллипсоида. Так как уровенная поверхность радиусом до 20 км может быть заменена плоскостью, при относительно небольших площадях, точки местности проецируют на горизонтальную плоскость. Положение полученных проекций точек может быть определено координатами.

_______В результате перенесения точек на плоскость длины линий заменяют их горизонтальными проекциями, называемыми горизонтальными проложениями; пространственные углы заменяются плоскими, и вся фигура заменяется проекцией на горизонтальную плоскость (рис. 2).

Системы координат, принятые в геодезии

_______В геодезии применяются следующие системы координат:

• Географическая система координат,
• Зональная система плоских прямоугольных координат Гаусса–Крюгера,
• Полярная система координат.

4.1. Географические координаты

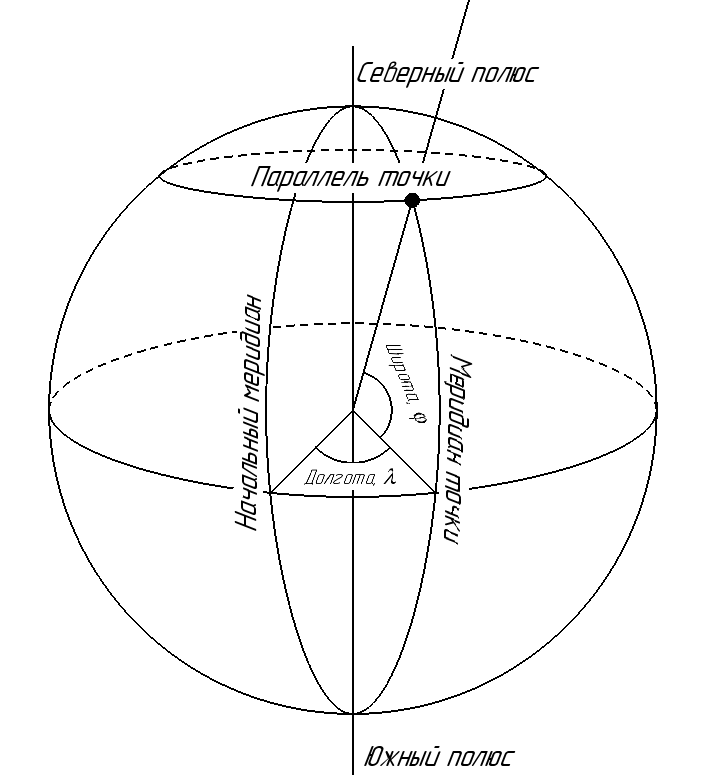_______С помощью географических координат, то есть широт (φ) и долгот (λ), определяют положение точки относительно экватора и начального меридиана.

_______Широтой (φ) точки называется угол, составленный отвесной линией в данной точке и плоскостью экватора.

_______Долготой (λ) точки называется двугранный угол между плоскостью меридиана данной точки и плоскостью начального меридиана.

https://vk.com/video_ext.php

_______Широта отсчитывается по дуге меридиана к северу и к югу от экватора от 0° до 90°. К северу от экватора широта называется северной, к югу – южной.

_______Долгота отсчитывается от меридиана, проходящего через Гринвич на окраине Лондона. Долгота отсчитывается по дуге экватора или параллели от начального меридиана в сторону востока и запада от 0° до 180°. Долгота к востоку от Гринвичского меридиана называется восточной долготой, к западу – западной. Широты и долготы определяют положение любой точки на земной поверхности и выражаются в угловой мере. Географические координаты определяются из астрономических наблюдений и, а также с помощью геодезических измерений.

4.2. Зональная система плоских прямоугольных координат Гаусса–Крюгера

_______При геодезических работах на больших территориях применяется зональная система плоских прямоугольных координат Гаусса–Крюгера (рис. 4). Для этого земной шар делится меридианами на шестиградусные или трехградусные зоны (рис. 3). Счет зон ведется к востоку от Гринвичского меридиана. Каждая зона проецируется на плоскость таким образом, чтобы средний меридиан зоны был изображен прямой линией. Средний меридиан зоны называется осевым меридианом.

_______Изображение осевого меридиана принимается за ось абсцисс (x), изображение экватора – за ось ординат (y). За начало координат принимают точку пересечения осевого меридиана с экватором.

_______Чтобы не иметь отрицательных ординат, ординату осевого меридиана принимают равной 500 км. Перед ординатой точки указывается номер зоны, в которой точка расположена.

Поперечный масштаб

Основание AB нормального поперечного масштаба равно, как и в линейном масштабе, также 2 см. Наименьшее деление основания равно CD =1/10 АВ= 2мм. Наименьшее деление поперечного масштаба равно cd = 1/10 CD =1/100 АВ = 0,2мм (что следует из подобия треугольника BCD и треугольника Bcd).

Таким образом, для численного масштаба 1:2000 основание поперечного масштаба будет соответствовать 40 м, наименьшее деление основания (1/10 основания) равно 4 м, а наименьшее деление масштаба 1/100 АВ равно 0,4 м.

Пример: отрезок ав (рис. 2), взятый с плана масштаба 1:2000, соответствует на местности 137,6 м (3 основания поперечного масштаба (3х40=120 м), 4 наименьших деления основания (4х4=16 м) и 4 наименьших деления масштаба (0.4х4=1.6 м), т.е. 120+16+1.6=137.6 м) .

Остановимся на одной из важнейших характеристик понятия «масштаб».

Точностью масштаба называется горизонтальный отрезок на местности, который соответствует величине 0,1 мм на плане данного масштаба. Эта характеристика зависит от разрешающей способности невооруженного человеческого глаза, которая (разрешающая способность) позволяет рассмотреть минимальное расстояние на топографическом плане в 0.1мм. На местности эта величина будет уже равна 0.1 мм х М, где М – знаменатель масштаба.

Рис.2

Поперечный масштаб, в частности, позволяет измерить длину линии на плане (карте) масштаба 1:2000 именно с точностью данного масштаба.

Пример: в 1 мм плана 1:2000 содержится 2000 мм местности, а в 0,1мм, соответственно, 0,1 x М (мм) = 0.1 х 2000 мм = 200 мм = 20 см, т.е. 0,2 м.

Поэтому при измерении (построении) на плане длины линии ее значение следует округлить с точностью масштаба. Пример: при измерении (построении) линии длиной 58,37 м (рис. 3), ее значение в масштабе 1:2000 (с точностью масштаба 0,2 м) округляется до 58,4 м, а в масштабе 1:500 (точность масштаба 0,05 м) – длина линии округляется уже до 58,35 м.

Вычисление дирекционных углов

По известному дирекционному углу a_n и по исправленным горизонтальным углам b_испр вычисляются дирекционные углы остальных сторон теодолитного хода по формулам для правых горизонтальных углов:

– дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус исправленный горизонтальный угол правый по ходу.

Величина дирекционного угла не может превышать 360° и быть меньше 0°. Если величина дирекционного угла больше 360°, то из результата вычислений необходимо вычесть 360° (см. пример).

Контроль вычисления дирекционных углов. В замкнутом теодолитном ходе в результате вычислений получается дирекционный угол исходной стороны.

Пример вычисления дирекционных углов:

Дирекционный угол исходной стороны a_1-2равен 45°45¢.

При вычислении дирекционного угла получилось значение 405°45¢. Из полученного значения вычитается 360°.

Контроль вычисления дирекционных углов получился.

Все результаты вычислений заносятся в таблицу «Ведомость вычисления координат» (табл. 2).

1.3 Вычисление приращений координат

Вычисление приращений координат выполняется по формулам:

,

где d – горизонтальное проложение (длина) линии; a – дирекционный угол этой линии.

Приращения координат вычисляются с точностью два знака после запятой.

Пример вычисления приращений координат:

Все результаты вычисления заносятся в табл. 2. Пример вычисления тригонометрических функций на калькуляторе приведен в отдельном файле.

1.4 Уравнивание линейных измерений

Разность между суммой вычисленных приращений координат и теоретической суммой называется линейной невязкой хода и обозначается f_Х и f_Y. Уравнивание линейных измерений выполняется по осям Х и Y.

Линейная невязка вычисляется по формулам:

Теоретическая сумма приращений координат зависит от геометрии хода. В замкнутом теодолитном ходе она равна нулю, тогда невязка равна

Прежде, чем распределять невязки в приращения координат, необходимо убедиться в их допустимости. Для чего вычисляется абсолютная невязка хода f_абс

,

где Р – периметр хода (сумма длин сторон), м.

Относительная невязка сравнивается с допустимой .

В случае, когда полученная относительная невязка допустима, т.е. , то вычисляются поправки в приращения координат пропорционально длинам сторон. Невязки распределяются с обратным знаком. Если , то проверяются вычисления в п. 3.3 и 3.4.

Поправки в приращения координат d_X и d_Y вычисляются по формулам с округлением до 0,01 м:

,

где d_X и d_Y – поправка в приращение по оси Х и Y, соответственно, м; f_X и f_Y – невязки по осям, м; Р – периметр (сумма сторон), м; d_i – измеренная длина (горизонтальное проложение), м.

Знак у поправки противоположен знаку невязки. Поправки записываются в «Ведомость вычисления координат». В примере (табл. 6) поправки показаны красным цветом.

После вычисления поправок следует сделать проверку, т.е. сложить все поправки. Если их сумма будет равна невязке с обратным знаком, то распределение невязки выполнено правильно. То есть:

Вычисляются исправленные приращения.

Полученные поправки алгебраически прибавляются к соответствующим приращениям и получаются исправленные приращения:

Контроль: сумма исправленных приращений в замкнутом теодолитном ходе должна равняться нулю, т.е. должно выполняться равенство:

Пример вычисления линейной невязки:

Пример вычисления поправок в приращения координат:

Контроль .

Контроль .

Поправки записываются в «Ведомость вычисления координат» над вычисленными приращениями. В примере поправки показаны красным цветом (Табл. 2).

Пример вычисления исправленных приращений координат:

Контроль ; Контроль .

Сумма исправленных приращений равна нулю, т.е. контроль выполняется.

Дирекционный угол

Дирекционный угол (α) – это угол между проходящими через данную точку направлением на ориентир и линией параллельной оси абсцисс, отчитываемой от северного направления оси абсцисс по ходу часовой стрелки оси 0 до 360°.

Дирекционные углы направлений измеряются преимущественно по карте или определяются по магнитным азимутам.

Дирекционный угол ориентирного направления может определяться геодезическим или гироскопическим способом, из астрономических наблюдений, с помощью магнитной стрелки буссоли и по контурным точкам карты (аэрофотоснимка).

При геодезическом способе ориентирования дирекционный угол ориентирного направления может быть получен непосредственно из каталога (списка) координат, решением обратной геодезической задачи по координатам геодезических пунктов, при выполнении засечек или прокладке полигонометрического хода одновременно с определением координат привязываемых точек, а также путем передачи угловым ходом от направления с известным дирекционным углом.

При гироскопическом способе ориентирования с помощью гирокомпаса определяют истинный (астрономический) азимут ориентирного направления, а затем переходят к дирекционному углу этого направления. Азимут ориентирного направления с помощью гирокомпаса определяется по двум, трем (четырем) точкам реверсии. Увеличение числа точек реверсии до трех (четырех) обеспечивает контроль и повышает точность определения дирекционного угла.

При астрономическом способе ориентирования дирекционный угол ориентирного направления определяют путем перехода от азимута светила к азимуту ориентирного направления, а от последнего — к дирекционному углу. Азимут светила вычисляют по результатам наблюдений, выполненных на местности с данной точки. Азимут ориентирного направления из астрономических наблюдений может быть получен и с помощью азимутальной насадки АНБ-1 к буссоли ПАБ-2А непосредственно на местности без выполнения вычислений.

Способ определения дирекционного угла ориентирного направления из астрономических наблюдений является наиболее точным.

Работы в поле при этом способе заключаются в измерении горизонтального угла Q между направлением на светило и заданным направлением в момент времени наведения прибора на светило. По моменту времени наблюдения светила вычисляют азимут а светила, от него переходят к астрономическому азимуту А направления на ориентир: A’ = a + Q. Зная значение сближения меридианов у в точке наблюдения, определяют дирекционный угол с ориентирного направления: a = A — y.

При определении дирекционного угла ориентирного направления с помощью магнитной стрелки буссоли на местности сначала получают магнитный азимут ориентирного направления, а затем, учитывая поправку буссоли, переходят к дирекционному углу. Дирекционный угол ориентирного направления определяется по формуле: а = Ат + (±dАт).

По карте (аэрофотоснимку) дирекционный угол ориентирного направления получают решением обратной геодезической задачи по координатам двух контурных точек Координаты контурных точек при этом определяются по карте (аэрофотоснимку) с помощью циркуля измерителя и поперечного масштаба. Точность полученного дирекционного угла будет тем выше, чем больше расстояние между начальной и ориентирной точками и чем точнее определены координаты этих точек.

Дирекционный угол по карте также можно определить с помощью хордоугломера. Для этого опознают на карте исходную и ориентирную точки, проводят через них прямую линию и получают на карте ориентирное направление. Измерив с помощью хордоугломера угол между северным направлением вертикальной линии километровой сетки карты и ориентирным направлением, получают дирекционный угол этого направления.

Свойства дирекционных углов: дирекционные углы α₁=α₂=α₃ так как параллельные линии пересекаются одной линией. Следовательно, углы равны.

Рисунок 2. — Дирекционные углы.

Дирекционные углы могут быть прямыми и обратными (они отличаются на 180°):

Рисунок 3. — Прямые и обратные дирекционные углы.

В зависимости от выбора системы поверхностных координат или проекции земного эллипсоида на плоскость дирекционный угол может иметь собственное название. Например, геодезическийдирекционный угол, гауссов дирекционный угол и т.д.

Численным масштабом

Численный масштаб – величина неименованная. Он записывается так: 1:1000, 1:2000, 1: 5000 и т.д., причём в такой записи 1000, 2000 и 5000 называется знаменателем масштаба М.

Численный масштаб говорит о том, что в одной единице длины линии на плане (карте ) содержится точно столько же единиц длины на местности. Так, например, в одной единице длины линии на плане 1:5000 содержится точно 5000 таких же единиц длины на местности, а именно: один сантиметр длины линии на плане 1:5000 соответствует 5000 сантиметрам на местности (т.е. 50 метрам на местности); в одном миллиметре длины линии на плане 1:5000 содержится 5000 миллиметров на местности (т.е. в одном миллиметре длины линии на плане 1:5000 содержится 500 сантиметров или 5 метров на местности) и т.д.

При работе с планом в ряде случаев пользуются линейным масштабом.

Измерения на местности

Магнитный азимут направления определяется с помощью компаса. При этом отпускают тормоз магнитной стрелки и поворачивают компас в горизонтальной плоскости до тех пор, пока северный конец стрелки не установится против нулевого деления шкалы. Затем, не меняя положения компаса, устанавливают визирное приспособление так, чтобы линия визирования через целик и мушку совпала с направлением на предмет. Отсчет шкалы против мушки соответствует величине определяемого магнитного азимута направления на местный предмет.
На рисунке магнитный азимут на отдельное дерево равен 330°.

Рис. Определение магнитного азимута по компасу.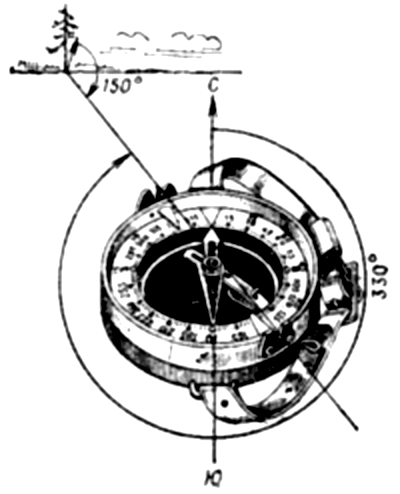

Ориентирование на местности по азимутам

Азимут направления с точки стояния на местный предмет называется прямым магнитным азимутом. Для определения направления на местности по заданному магнитному азимуту необходимо установить на шкале компаса против мушки отсчет, равный значению заданного магнитного азимута. Затем, отпустив тормоз магнитной стрелки, повернуть компас в горизонтальной плоскости так, чтобы северный конец стрелки установился против нулевого деления шкалы. После этого, не меняя положения компаса, заметить на местности по линии визирования через целик и мушку какой-нибудь удаленный ориентир. Направление на ориентир и будет определяемым направлением, соответствующим заданному азимуту.

Совмещение визирной линии с направлением на предмет (цель) достигается многократным переводом взгляда с визирной линии на цель и обратно. Не рекомендуется поднимать компас до уровня глаз, так как в этом случае снижается точность измерения. Точность измерения азимутов с помощью компаса Андрианова составляет плюс-минус 2-3°.

Решение прямой и обратной геодезической задачи

Суть прямой геодезической задачи состоит в том, чтобы определить координатные значения вершины при заданных координатах соседней. Это возможно при известной горизонтальном проложении между ними и дирекционным углом линии. Для ее решения используются следующие формулы:

\(\Delta X=d\cdot cos \alpha \)

\(\Delta Y=d\cdot sin \alpha \)

где:

Создавайте будущее вместе с нами

Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.

\(d\)–расстояния между соседними пунктами.

\(\alpha \) – значение дирекционного угла.

Знаки приращений зависят от четверти, определяемой дирекционным углом направления. Координатные значения конечной точки линии равняется сумме координаты начальной и приращения между ними. Из этого следует следующие выражение:

\(X_{2}=X_{1}+\Delta X\)

\(Y_{2}=Y_{1}+\Delta Y\)

\(X_{2}=X_{1}+d_{1-2}\cdot cos\alpha _{1-2}\)

\(Y_{2}=Y_{1}+d_{1-2}\cdot sin\alpha _{1-2}\)

Стоит также упомянуть и обратную геодезическую задачу, которая позволяет определить дирекционный угол, румб и горизонтальное проложение при установленных координатах пунктов теодолитного хода. Вычисления имеют такую последовательность:

\(\Delta X=X_{2}-X_{1}\)

\(\Delta Y=Y_{2}-Y_{1}\)

определяется румб линии \(r_{1-2}\):

\(tgr=\frac{\Delta Y}{\Delta X}\)

из этого выходит, что:

\(r=arctg\frac|{\Delta Y}{\Delta X}|\)

По знакам приращения определяют четверть, в котором находится направление и по уже известному румбу вычисляют дирекционный угол. Определение горизонтального проложения будет завершающим этапом в решении обратной задачи:

\(d=\frac{\Delta X}{cos\alpha }\)

\(d=\frac{\Delta Y}{sin\alpha }\)

\(d=\sqrt{\Delta X^2+\Delta Y^2}\)

Измерения на карте

Измерение расстояний

Важной задачей при работе с картой является измерение расстояний. Прямые линии измеряют обычно линейкой

Извилистые и ломаные линии измеряют по частям, циркулем — измерителем. Для этого устанавливают по линейке или линейному масштабу раствор циркуля, соответствующий какому-нибудь целому числу километров или сотен метров, и таким «шагом» проходят вдоль измеряемой линии, ведя счёт перестановок ножек.

Рис. Измерение линий «шагом» циркуля.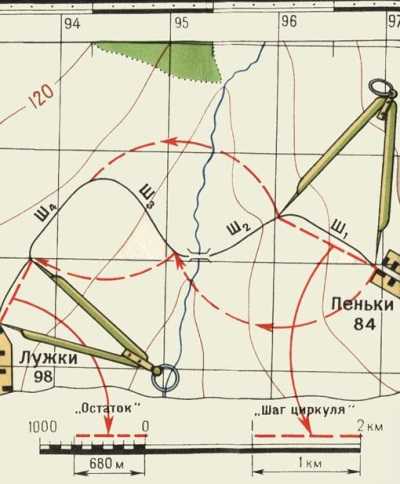

Величину «шага» выбирают в зависимости от извилистости линий: от 4-5 см — при измерении кривых с плавными закруглениями до 1-2 см — при измерении линий с большим числом резких поворотов.

Рис. Измерение расстояния с помощью линейного масштаба и циркуля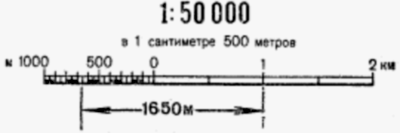

Для измерения кривых и извилистых линий используют также специальный прибор — курвиметр. При движении колёсика вдоль измеряемой по карте линии стрелка передвигается по циферблату и указывает пройденное колёсиком расстояние в см. Для измерения расстояния следует предварительно вращением колёсика установить стрелку курвиметра в начальное положение, т.е. на отсчёт «0», а затем прокатить его вдоль измеряемой линии, следя за тем, чтобы стрелка двигалась по циферблату в направлении чисел 10, 20, 30 и т.д. Умножив величину масштаба карты на показания стрелки курвиметра, получают расстояние на местности.

Рис. Курвиметр.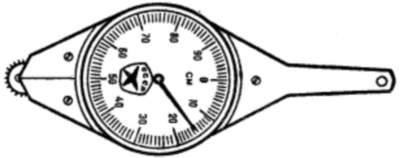

Измерение углов

Какие углы мы можем измерить по карте:

Дирекционный угол – угол между северным направлением вертикальной сетки и направлением на объект. Можно измерить по карте транспортиром.

Истинный азимут – горизонтальный угол, измеряемый по ходу часовой стрелки между северным направлением истинного меридиана и направлением на объект. (Можно измерить по карте транспортиром или пересчитать из дирекционного угла)

Магнитный азимут – горизонтальный угол, измеряемый по ходу часовой стрелки между северным направлением магнитного меридиана и направлением на объект. Измеряется компасом на местности.

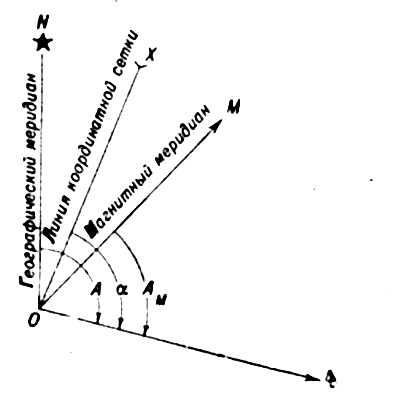
• α – дирекционный угол;
• А – истинный азимут;
• АМ – магнитный азимут.

Все углы связаны, измерив один, можно перейти к другим:

• Аи – истинный азимут
• Ам – магнитный азимут
• ДУ – дирекционный угол
• Ск – магнитное склонение
• Сб – сближение меридианов
• Пн – поправка направления

Аи=Ам+(Ск) Ам=Аи-(Ск) Ам=ДУ- (Пн) Пн=Ск-(Сб)

Азимут какой-либо линии АВ, определенный в начальной точке А, называется прямым. Азимут той же линии, определенный в её конечной точке В, называется обратным. Он равен прямому азимуту 180.

Дирекционные углы измеряют транспортиром. Исходную точку и местный предмет (цель) соединяют прямой линией, длина которой от точки ее пересечения с вертикальной линией координатной сетки должна быть больше радиуса транспортира. Затем совмещают транспортир с вертикальной линией координатной сетки, сообразуясь с величиной угла. Отсчет по шкале транспортира против прочерченной линии будет соответствовать величине измеряемого дирекционного угла. Средняя ошибка измерения угла транспортиром офицерской линейки составляет 0,5° (0-08).

Рис. Измерение дирекционного угла транспортиром.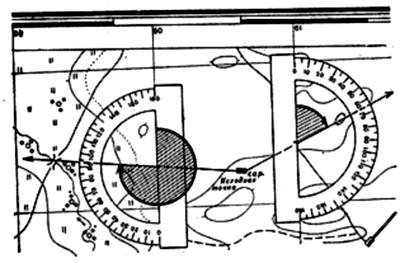

Чтобы провести на карте направление, заданное дирекционным углом в градусной мере, надо через главную точку условного знака исходного пункта провести линию, параллельную вертикальной линии координатной сетки. К линии приложить транспортир и против соответствующего деления шкалы транспортира (отсчета), равного дирекционному углу, поставить точку. После этого через две точки провести прямую линию, которая и будет направлением данного дирекционного угла. Артиллерийским кругом дирекционные углы на карте измеряют так же, как и транспортиром. Центр круга совмещают с исходной точкой, а нулевой радиус — с северным направлением вертикальной линии координатной сетки или параллельной ей прямой. Против прочерченной на карте линии считывают по красной внутренней шкале круга значение измеряемого дирекционного угла в делениях угломера. Средняя ошибка измерений артиллерийским кругом составляет 0-03(10′).

Съемки

_______Для составления планов и карт необходимо на местности производить геодезические измерения. Комплекс таких измерений называется съемкой.

теодолитнойтахеометрическойфототопографическойполевыми работамикамеральной обработкой

Тест

Инструкция по прохождению теста

• Выберите один из вариантов в каждом из 10 вопросов;
• Нажмите на кнопку «Показать результат»;
• Скрипт не покажет результат, пока Вы не ответите на все вопросы;
• Загляните в окно рядом с номером задания. Если ответ правильный, то там (+). Если Вы ошиблись, там (-).
• За каждый правильный ответ начисляется 1 балл;
• Оценки: менее 5 баллов — НЕУДОВЛЕТВОРИТЕЛЬНО, от 5 но менее 7.5 — УДОВЛЕТВОРИТЕЛЬНО, 7.5 и менее 10 — ХОРОШО, 10 — ОТЛИЧНО;
• Чтобы сбросить результат тестирования, нажать кнопку «Сбросить ответы»;

Нанесение точек на план и его оформление

После завершения обработки измерений, которые были проведены на местности, составляется ее контурный или ситуационный план. Построение плана теодолитного хода происходит поэтапно и состоит из следующих этапов:

1. Создание координатной сетки. Ход необходимо равномерно отобразить на плане, поэтому сначала определяют середину листа. Через весь лист проводят два диагональных отрезка, от которых и будет строиться сетка, состоящая из отрезков по 10 см. Допускается погрешность не более 0,2 мм. Определить их количество можно по формуле:

\(N_{X}=(x_{max}-x_{min})/200\)

\(N_{Y}=(y_{max}-y_{min})/200\)

\(x_{max},y_{max}\) – наибольшие значения координат, увеличенные до большего значения, которое кратное 200.

\(x_{min},y_{min}\) – наименьшее значение, но уменьшенное и кратное 200.

200 – длина стороны квадрата в метрах , которая в плане равна 10 см.

2. Обозначение точек на плане. Лучше всего подходят для нанесения координат пунктов на план циркуль и масштабная линейка. Соседние вершины должны иметь такое же расстояние и дирекционный угол, как записано в ведомости.
3. Нанесение ситуации на план. Участки снимаемой местности в процессе полевых работ отображают на специальном схематическом бланке – абрисе. В дальнейшем их используют для переноса контуров, линий и вершин точек. Ситуация изображается на планах и картах специальными обозначениями – условными знаками.
4. Оформление плана в соответствии с требованиями. Все топографические материалы должны строго соответствовать нормативным документам. В частности, нужно выдерживать заданные очертания и их размеры. Должны присутствовать пояснительные надписи, легенда, а также указан масштаб.

Сегодня координаты замкнутого теодолитного хода вычисляются значительно проще, а создание всех графических материалов выполняется при помощи специализированных программ автоматически. Это значительно ускорило процесс выполнения геодезических работ и других инженерных изысканий.

Определение прямоугольных координат точек

На топографических планах наносится координатная сетка, образующая квадраты со сторонами 10 см. Вертикальные линии сетки параллельны оси абсцисс, а горизонтальные — оси ординат. Координаты вершин квадратов координатной сетки подписываются.
Для быстрого нахождения какой-нибудь точки на топографическом плане указывают нижний левый угол соответствующего квадрата сетки координат.

Пример: запись 79,2 означает, что абсцисса линии сетки Х = 79,2 км, т.е. отстоит по оси Х от начала координат на 79200 м. Запись 66,2 означает, что ордината линии сетки Y = 66,2 км, т.е. отстоит по оси У от начала координат на 66200 м.

Для быстрого нахождения какой-нибудь точки на топографическом плане указывают нижний левый угол соответствующего квадрата сетки координат.

Пример: пользуясь координатной сеткой, циркулем и поперечным масштабом, по топографическому плану можно определить прямоугольные координаты точки А (рис. 4), находящейся в квадрате 79,2 – 66,2. Необходимо помнить, что абсциссы возрастают к северу, а ординаты — к востоку.

Сначала записывают в метрах абсциссу Х (южной) линии квадрата, в котором находится точка А, т.е. Х(южной линии сетки) =79200,0 м. Циркулем и поперечным масштабом определяют расстояние Δх = Y(а)-Y(А) также в метрах с точностью масштаба. Полученную величину Δх=64,8 м прибавляют к абсциссе нижней (южной) линии квадрата Х(южной линии сетки) =79200,0 м и находят абсциссу точки А: Х(А) = 79200,0 + 64,8 = 79264,8 м.

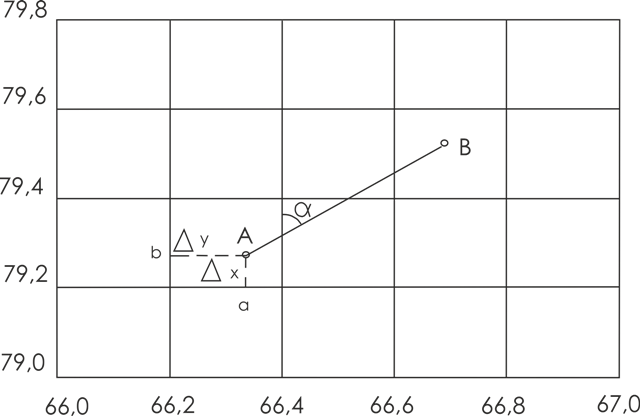
Рис.4

Общие понятия о системах координат в геодезии

Столь глубокие познания о строении и форме Земли, которые человек осваивал на протяжении веков, сегодня позволяют создавать невероятно точные координатные системы и картографические проекции.

Координатные системы заданы двумя направлениями на плоскости, а в пространстве – тремя. Осевые направления всегда перпендикулярны друг другу, а ориентированы горизонтально и вертикально. Их пересечение и определяет местоположение точки в заданной системе.

В геодезии координатные системы разделены на следующие две группы:

1. Прямолинейные прямоугольные. К ним причисляют проекцию Гаусса-Крюгера, индивидуальные референцные и местные системы.
2. Полярные. Это геодезические, географические, астрономические, а также геоцентрические и топоцентрические координаты.

Теодолитный ход можно считать самым распространённым плановым обоснованием. Он не требует дорогостоящего и высокоточного оборудования, но помогает создать надежную плановую основу на территориях со сложной местностью. Его развивают от пунктов государственных геодезических сетей (ГГС) и сетей сгущения с уже установленными координатами.

Вычисляются координаты точек замкнутого и разомкнутого теодолитного хода посредством нахождения дирекционных углов его сторон и решения прямой геодезической задачи. Но перед этим следует проверить, соответствуют ли измерения нормативным требованиям.

8 Углы ориентирования линий. Истинный и магнитный азимуты, и связь между ними

При выполнении геод работ на местности,
работ с картой чертежем необходимо
определить положение линий относительно
стран света или какого-нибудь напрвления
принятого за исходное.

Ориентирование
заключается в том что определяют угол
между исходным направлением и направлением
данной линии. За исходное направление
принимают истинный ( неогр), магнитный
меридианы или ось абсцисс прямоугольнойсистемы
координат плана.

В качестве углов,
определяющих направление линий, служат
истинный и магнитный азимуты, дирекционный
угол и румбы. Угол между северным
направлением меридиана и направлением
данной линии наз азимутом. Измеряется
по направлению движения часовой стрелки.
От 0-360 град.

Зависимость между прямым и обратным
азимутами линии МН А1=А+180ГРАД + СБЛИЖЕНИЕ.

Исходные данные для расчетов

Теодолитный ход может быть проложен в виде замкнутой фигуры или ломаной линии. Это зависит от характера снимаемой местности. Он является отличной геодезической основой для многих инженерных изысканий.

По итогу проведенных измерений составляется план или карта местности, а все вычисления заносятся в специальные ведомости. В нее заносятся следующие данные:

– горизонтальные углы пунктов;

– измеренное расстояние между ними;

– координаты пункта ГГС или опорной сети;

– значение исходного дирекционного угла.

Для привязки хода к пункту ГГС или опорной сети необходимо определить местоположение одной его точки относительно этого пункта. Это можно сделать, измерив расстояние и горизонтальный примычной угол между ними. Такая процедура называется передачей координат и дирекционных углов.

Приращение координат и их увязка

Приращением называют величины, на которые будут увеличены координаты предыдущей точки для вычисления последующей. В основу этих расчетов берется уже знакомая формула прямой задачи:

\(\Delta X=d\cdot cos \alpha \)

\(\Delta Y=d\cdot sin \alpha \)

Полученные значения также необходимо уровнять, чтобы равномерно распределить погрешности и получить наиболее точный результат. Начинают расчеты с определения невязок. Поскольку сумма проекций в сторонах многоугольной замкнутой фигуры равняется нулю, для вычисления невязок пунктов замкнутого хода используют следующую формулу:

\(f_{X}=\sum \Delta X_{выч}-\sum \Delta X_{теор};\sum \Delta X_{теор}=0\)

\(f_{Y}=\sum \Delta Y_{выч}-\sum \Delta Y_{теор};\sum \Delta Y_{теор}=0\)

\(\sum \Delta X_{выч},\sum \Delta Y_{выч}\) – суммы приращений, рассчитанные с учетом знаков для замкнутого и разомкнутого хода;

\(\sum \Delta X_{теор},\sum \Delta Y_{теор}\) – теоретические суммы приращений.

Вследствие влияния погрешностей на ход, он будет разомкнут на величину , которая представляет собой абсолютную невязку в его периметре. По этому причине проверяется соответствие условию допустимости его невязок.

1. Абсолютное значение:

\(f_{p}=\sqrt{f_{x}^2+f_{y}^2}\)

2. Относительное

\(f_{отн}=\frac{f_{абс}}{P}\)

P – периметр хода, полученный суммированием всех его сторон.

Допустимая невязка должна удовлетворять условие 1/2000, а при соответствии выражению \(|f_{отн}|\leq |f_{доп}|\) выполняют ее распределение с противоположным знаком. Однако перед этим рассчитывают поправки приращений, которые определяют для каждой стороны:

\(\delta _{x_{i}}=-\frac{f_{x}d_{i}}{P}\);\(\delta _\Delta {y_{i}}=-\frac{f_{y}d_{i}}{P}\)

\(\delta _{x_{i}},\delta _{y_{i}}\)– значения поправок в приращениях.

Чтобы упростить дальнейшие расчеты поправки, необходимо округлить их до 0,01 м.

Для разомкнутого хода за теоретическую сумму приращений берется разность между двумя соседними точками.

\(f_{X}=\sum \Delta X_{выч}-\sum \Delta X_{теор};   \sum \Delta X_{теор}=x_{B}-x_{A}\)

\(f_{Y}=\sum \Delta Y_{выч}-\sum \Delta Y_{теор};   \sum \Delta Y_{теор}=y_{B}-y_{A}\)

Для обоих ходов поправки имеют противоположный приращению знак. Уравнивание выполнено верно, если сумма исправленных приращений равна или максимально приближена к нулю.