Построение корневого локуса

Построение — корневой годограф

Построение корневого годографа базируется на расположении полюсов и нулей KGH в s — шюскости. Эти точки не перемещаются. Они являются просто конечными точками годографа корней 1 K. Если годограф пересекает мнимую ось при некотором значении коэффициента усиления К, система становится неустойчивой при этом значении К — Степень устойчивости определяется главным образом корнями, наиболее близко расположенными к мнимой оси. Набросок корневого годографа дает инженеру представление о форме годографа и облегчает построение более точного графика.
 

Определение положения.

Построение корневого годографа в случае, когда варьируемым параметром является постоянная времени, требует преобразований характеристического уравнения системы.
 

Построение корневых годографов не требует вычисления корней характеристического уравнения замкнутой системы для разных значений К и может быть существенно упрощено, если принять во внимание ряд характерных свойств годографов.
 

Построение корневых годографов целесообразно не только-для выяснения вопроса устойчивости системы. Построенные корневые годографы, как это будет показано в соответствующих разделах, позволяют рассчитывать законы изменения переменных системы при некоторых типовых воздействиях, а также выяснить, как влияет на устойчивость и динамические характеристики системы изменение варьируемого параметра. Представить характеристическое уравнение в виде (5.9) нетрудно.
 

Построение корневых годографов по этому параметру, помимо выяснения вопроса ус1оЙ4НБис1и, позволяет установить предельное значение Л, при котором система при всех остальных постоянных значениях еще останется устойчивой.
 

Метод построения корневых годографов и основан на нахождении всех точек пл.
 

При построении корневого годографа пользуются определенными правилами, вытекающими из его свойств и облегчающими процесс определения траектории движения полюсов передаточной функции замкнутой системы.
 

При построении корневых годографов системы автоматического регулирования полезно знать основные свойства, которыми они обладают. Ниже без доказательства приводятся некоторые свойства корневых годографов.
 

Наиболее простым построение корневого годографа будет в том случае, когда рассматриваемый параметр А входит в характеристическое уравнение линейно.
 

Годографы систем с сопряженными ком.

Изложенный порядок построения корневых годографов иллюстрируется примерами, приведенными в конце параграфа.
 

Для облегчения построения корневого годографа обычно выбирают упрощенную передаточную функцию

При этом важно отразить наличие вещественных и комплексно сопряженных корней.
 . Таким образом, построение корневых годографов можно производить без вычисления корней характеристического уравнения системы, пользуясь лишь характерными особенностями таких годографов; характер корневых годографов позволяет судить о качественных показателях системы.
 

Таким образом, построение корневых годографов можно производить без вычисления корней характеристического уравнения системы, пользуясь лишь характерными особенностями таких годографов; характер корневых годографов позволяет судить о качественных показателях системы.
 

Продолжим рассмотрение этапов построения корневого годографа.
 

Годограф Михайлова в научных исследованиях

Годограф Михайлова — это графический метод анализа динамических систем, который используется в научных исследованиях различных областей знания. Такой метод позволяет визуализировать и анализировать поведение системы в зависимости от изменения параметров и внешних воздействий.

Основной принцип построения годографа Михайлова заключается в построении траектории точки на комплексной плоскости в зависимости от частоты. Для этого необходимо изучить переходную функцию системы и анализировать ее полюса и нули.

Использование годографа Михайлова в научных исследованиях позволяет:

1. Анализировать стабильность системы. Годограф Михайлова позволяет определить, при каких значениях параметров система будет стабильной. Анализ полюсов системы позволяет определить, насколько система устойчива.
2. Изучать динамические свойства системы. Годограф Михайлова позволяет определить режимы работы системы и исследовать их изменение при изменении параметров системы.
3. Анализировать влияние внешних воздействий. Годограф Михайлова позволяет изучать, как внешние сигналы влияют на поведение системы и какие изменения происходят с траекторией точки при изменении частоты.
4. Оптимизировать параметры системы. Годограф Михайлова позволяет определить оптимальные значения параметров системы для достижения заданных характеристик.

В научных исследованиях годограф Михайлова применяется в таких областях, как электротехника, механика, автоматика, теория управления и другие. Он является мощным инструментом для анализа и оптимизации систем, помогая исследователям лучше понять их динамику и поведение.

Таким образом, годограф Михайлова является важным методом в научных исследованиях, который позволяет проводить анализ и оптимизацию динамических систем в различных областях науки и техники.

Определение устойчивости типа деформаций (понятие о явлении потери устойчивости)

Устойчивостью называется способность сооружений сохранять свое первоначальное положение или первоначальную форму равновесия в деформированном состоянии при действии внешних сил.

В соответствии с этим надо различать устойчивость положения сооружения и устойчивость форм равновесия в нагруженном состоянии.

Положение сооружения или форма равновесия в нагруженном состоянии считаются устойчивыми, если при всяком, сколь угодно малом дополнительном возмущении, сооружение отклоняется от исследуемого положения или равновесного состояния, однако после исчезновения дополнительного возмущения полностью возвращается в исходное состояние (для упругих систем), или проявляет тенденцию к возвращению в исходное состояние (для упруго-пластических систем).

Положение сооружения или форма равновесия в нагруженном состоянии считаются неустойчивыми, если при каком-либо сколь угодно малом отклонении от исследуемого равновесном состоянии и после исчезновения возмущения сооружение не проявляет тенденцию к уменьшению получаемых отклонений, а иногда отклоняется еще далее — до нового положения или новой формы равновесного состояния.

Переход сооружения из одного равновесного состояния к другому равновесному состоянию называется потерей устойчивости системы. Состояние перехода называется критическим состоянием. При этом, величины внешних сил, действующие на сооружение называются критическими.

Как это следует из понятия устойчивости, в механике различают два вида потери устойчивости сооружения: потерю устойчивости положения и потерю устойчивости, вызванной сменой формы равновесного состояния.

При изучении потери устойчивости сооружений, связанная со сменой формы деформированного состояния в строительной механике различают два рода потери устойчивости.

Потерю устойчивости, связанную только со сменой формы деформированного состояния, называют потерей устойчивости первого рода, что свойственно только упругим системам.

Потерей устойчивости второго рода принято называть первое предельное состояние системы по несущей способности системы, т.е. состояние системы, когда при дальнейшем увеличении внешних сил равновесие между внешними и внутренними силами нарушается.

Основная задача теории устойчивости заключается в определении критических значений внешних сил. При этом наибольшее практическое значение имеет определение критических значений внешних сил при потере устойчивости системы по первому роду.

studopedia.ru

Устойчивость

«устойчивость»

Усто́йчивость — способность системы сохранять текущее состояние при влиянии внешних воздействий. Если текущее состояние при этом не сохраняется, то такое состояние называется неустойчивым.

• В макроэкономике устойчивость обозначает долгосрочное равновесие между эксплуатацией ресурсов и развитием человеческого общества.
• В метеорологии воздушная устойчивость относится к вертикальным перемещениям воздушных потоков.
• В технике устойчивость определяется как свойство технических систем сохранять значения конструктивных и режимных параметров в заданных пределах:
  • теплогидравлическая устойчивость — свойство канальных систем с обогревом потоков сохранять параметры движения и параметры теплопередачи.
  • нейтронно-теплогидравлическая устойчивость ядерных реакторов — свойство ядерных реакторов сохранять стабильность процессов тепловыделения и теплосьема в активной зоне.
• В механике устойчивость характеризуется ответом на малое возмущение системы, находящейся в механическом равновесии. Различают асимптотическую устойчивость, устойчивость по Ляпунову, экспоненциальную устойчивость, асимптотическую устойчивость в целом и др.
• В социологии также существует термин социальная устойчивость.
• На судах устойчивость (профессиональный термин — остойчивость) связана с восстанавливающим моментом и противодействием опрокидыванию.
• В теории автоматического управления устойчивость характеризуется реакцией динамической системы на внешние воздействия.
• В теории вероятностей определяют статистическую устойчивость как сходимость частот значений результатов измерения физической величины.
• В численном анализе устойчивость показывает, каким образом алгоритм связан с ошибками в вычислениях (см. численная устойчивость).
• В авиации устойчивость характеризует способность самолета без вмешательства пилота сохранять заданный режим полета (см. устойчивость и управляемость)
• В теории музыки — свойство, придающее звуку или системе звуков их постоянство.

ru.wikipedia.org

D (jω) = a0(jω)n + a1(jω)n-1 +…+ an-1(jω) + an .

В зависимости от степени числа (jω)nоно либо действительное, либо мнимое. По этой причине
частотный полином распадается на действительную часть U(ω) и мнимую часть V(ω):

D(jω) = U(ω) + j V(ω) ,(5.7)

U(ω) = a_n
— a_n-2ω2 +
a_n-4ω4 —…
(5.8)

V(ω) = a_n-1ω — a_n-3ω3+a_n-5ω5 -…. (5.9)

U(ω) – четная
функция ω, V(ω) – нечетная функция ω. По этому признаку полиномы (5.8) и
(5.9) можно назвать «четный» и «нечетный».

Задавая какое-либо значение частоты w₁ , из (5.8) и (5.9) получим
числа U(w₁) и V(w₁) . Вместе они образуют
комплексное число D(jw₁) . На комплексной плоскости оно
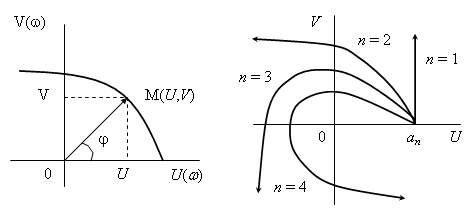
обозначается точкой М(U,V) , рис. 5.1.
Множество точек М(U,V) , отвечающих
разным частотам, образуют кривую, которая называется годографом Михайлова.

Рассмотрим годографы Михайлова для устойчивых систем.

В случае устойчивых систем годограф Михайлова имеет свойство
начинаться с точки U(0)
= a_n
, V(0) = 0. По
мере увеличения w
от нуля до бесконечности, точка М(U,V) перемещается влево так, что кривая стремится
охватить начало координат, одновременно удаляясь от него. Если провести
радиус-вектор из начала координат в точку М(U,V) , то окажется, что
радиус-вектор будет поворачиваться против часовой стрелки, непрерывно
увеличиваясь. Непрерывно увеличивается и угол, который он образует с осью
абсцисс. Представив комплексное выражение в экспоненциальной форме,

,

обнаруживаем,
что радиус-вектор есть модуль комплексного частотного полинома |D(jw)|
, а угол j(w)
– аргумент. Модуль имеет величину , аргумент равен .

Вид годографа Михайлова зависит от степени nхарактеристического
полинома. Годографы полиномов первых четырех степеней показаны на рисунках
далее. Они соответствуют устойчивым системам. Анализ годографов устойчивых
систем позволяет сделать выводы, которые и составляют содержание критерия
Михайлова.

Можно дать три формулировки критерию
Михайлова.

Первая формулировка

Если при изменении частоты от нуля до бесконечности
годограф Михайлова начинается на действительной оси в точке a_n,последовательно
проходит против часовой стрелки nквадрантов комплексной плоскости,
не проходя через ноль, и уходит в бесконечность в n-м квадранте, — система устойчива.

Вторая формулировка

Если при изменении частоты от нуля до бесконечности вектор
комплексного частотного полинома D(jw) последовательно
поворачивается против часовой стрелки на угол n(p/2), где n – степень
характеристического полинома, и нигде не становится нулем, — система устойчива.

Обратим внимание на частоты, при
которых годограф пересекает оси координат. Назовем их «частоты пересечения».
Первая частота нулевая, с нее начинается годограф

При w1
= 0 U(0) = an , V(0) = 0 . Вторая
отвечает точке пересечения годографом положительного отрезка оси ординат, U(w2)
= 0 , V(w2)
– некоторое число. Непрерывно увеличивая частоту, при некоторой, равной w3,
получим пересечение годографа с отрицательной частью оси абсцисс. Очевидно,
четвертым будет пересечение с отрицательной частью оси ординат при частоте w4.
Далее последуют частоты пересечения w5, w6,
…,wn. Все они действительные
положительные числа, каждое последующее больше предыдущего.

Третья формулировка критерия Михайлова

Если частоты пересечения годографа с осями координат
чередуются и образуют возрастающую последовательность вида ω₁ <
ω₂ < ω₃ <…<w_n, — система устойчивая.

В отличие от предыдущих, третья
формулировка позволяет исследовать устойчивость системы без построения
годографа, аналитически. Соображения следующие.

Каждому пересечению годографом действительной
оси (когда V(w) = 0) будет
соответствовать корень нечетного полинома V(w). Каждому
пересечению мнимой оси (когда U(w) = 0) будет
соответствовать корень четного полинома U(w). Следовательно,
по мере увеличения wкорни полиномов V(w) и U(w) для устойчивой
системы должны чередоваться (корень полинома V(w) сменяется корнем
полинома U(w) и т.д.); корень
каждого последующего пересечения оси должен быть больше предыдущего, все корни
должны быть действительными. Общее число корней равно степени
характеристического полинома.

В случае неустойчивых систем
кривые не охватывают начало координат, чередования частот нечетного и четного
полиномов нет.

Если годограф начинается из
начала координат или проходит через начало координат, система находится на
границе устойчивости.

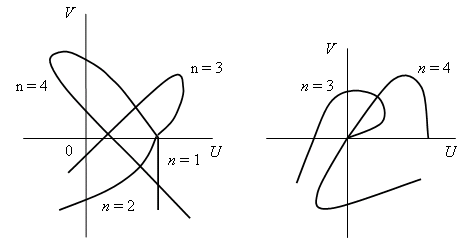
Создание основы годографа

Годограф Михайлова – графический метод, который позволяет визуально оценить устойчивость системы и проанализировать ее динамику. Для построения годографа необходимо следовать нескольким шагам:

1. Подготовьте данные.

Для построения годографа необходимо иметь передаточную функцию системы. Определите передаточную функцию, заданную в виде отношения полиномов:

W(s) = N(s)/D(s), где N(s) и D(s) – числитель и знаменатель полинома, соответственно. Найдите значения коэффициентов полиномов.

Убедитесь в устойчивости системы.

Проверьте наличие корней системы со значениями положительной вещественной части. Если такие корни существуют, система неустойчива, и годограф нельзя построить.

Разбейте полиномы на части.

Разбейте числитель и знаменатель полинома на простейшие блоки. Простейший блок имеет вид:

Ti = (s+a)^n

где Ti – простейший блок, n – показатель степени, а – константа.

Определите нули и полюса.

Найдите значения и координаты нулей и полюсов системы. Запишите значения в виде комплексных чисел: z = a + bj.

Постройте годограф.

Используя полученные значения нулей и полюсов, постройте годограф. Нули изображаются точками на Re-Im плоскости, а полюса – крестиками. Соедините нули и полюса касательными к фигуре, получив кривую, которая называется годографом.

Анализируйте график.

Изучите параметры и форму годографа. Анализируйте различные сценарии изменения параметров системы, используя годограф. Оцените устойчивость системы и степень свободы.

Следуя данным шагам, вы сможете построить годограф Михайлова и лучше понять динамику и стабильность вашей системы.

Годограф скорости

ГОДОГРАФ СКОРОСТИ. Пусть точка перемещается по некоторой траектории АВ. В каждый момент времени вектор скорости (v) направлен по касательной к траектории в соответствующем положении точки, причем v = dr/dt, где r — радиус-вектор, определяющий положение точки на кривой по отношению к некоторой системе отсчета с произвольным началом О (фиг. 1). Вектор ускорения (а) равен производной вектора (v) по времени (t) а = dv/dt. Если от некоторой произвольной точки О₁ откладывать векторы h = v, то, при перемещении точки по своей траектории, вектор (h) будет менять в общем как свою абсолютную величину, так и направление, имея одно и то же начало О₁. Конец вектора (h) будет описывать кривую, называемую годографом скорости. Так как вектор (h) для кривой А₁В₁ играет ту же роль, что вектор (r) для кривой АВ, то скорость конечной точки вектора (h), при ее перемещении по А₁В₁, равна

Таким образом, видно, что вектор ускорения точки, движущейся по некоторой траектории, равняется в каждый момент соответствующему вектору скорости конца вектора, описывающего годограф скорости. Плоскость, касательная к годографу скорости и проходящая через (h), будет, очевидно, параллельна плоскости, проходящей через (а) и (v), т. е. она будет параллельна соприкасающейся плоскости кривой АВ.

При прямолинейном равномерном движении (v = Const) годограф скорости стягивается в одну точку. Если точка перемещается по кривой, имея одну и туже линейную скорость (v = Const), то годограф скорости представляет собой кривую, описанную на шаровой поверхности радиуса (v).

При плоском движении, годограф скорости — плоская кривая. Для свободной материальной точки, брошенной под углом к горизонту с некоторой начальной скоростью v, имеем: v = v + gt, где v — вектор скорости точки по истечении времени (t), а g = Const — вектор ускорения силы тяжести. Так как h = v = Const, а вектор (gt) сохраняет постоянно вертикальное направление, то конец вектора (h = v) постоянно лежит на вертикали, т. е. годограф скорости для рассматриваемого случая представляет собой вертикальную прямую (фиг. 2).

Если точка описывает конического сечение с постоянной секториальной скоростью относительно фокуса конического сечения, то годограф скорости представляет собой окружность. Годограф скорости впервые был рассмотрен Гамильтоном, а затем Мёбиусом.

Определение устойчивости систем автоматического управления промышленными роботами

Необходимым условием работоспособности системы автоматического управления (САУ), является её устойчивость. Под устойчивостью принято понимать свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов после прекращения их воздействия .

Теория просто и кратко

Анализ устойчивости системы по методу Михайлова сводится к построению характеристического многочлена замкнутой системы (знаменатель передаточной функции), комплексной частотной функции (характеристического вектора):

(1)

где и – соответственно вещественная и мнимая части знаменателя передаточной функции, по виду которой можно судить об устойчивости системы.

Замкнутая САУ устойчива, если комплексная частотная функция , начинаясь на стрелки начало координат, проходя последовательно n квадрантов, где n – порядок характеристического уравнения системы, т. е.

(2)

Рисунок 1. Амплитудно-фазовые характеристики (годографы) критерия Михайлова: а) – устойчивой системы; б) – неустойчивой системы (1, 2) и системы на границе устойчивости (3)

САУ электроприводом манипулятора промышленного робота (МПР)

Рисунок 2 – Структурная схема САУ электроприводом МПР

Передаточная функция данной САУ имеет следующее выражение :

(3) где kу – коэффициент усиления усилителя, kм – коэффициент пропорциональности частоты вращения двигателя величине напряжения на якоре, Tу – электромагнитная постоянная времени усилителя, Tм – электромеханическая постоянная времени двигателя с учётом инерции нагрузки (по своим динамическим характеристикам двигатель представляет собой передаточную функцию последовательно соединённых инерционного и интегрирующего звеньев), kдс – коэффициент пропорциональности между входной и выходной величинами датчика скорости, K – коэффициент усиления главной цепи: .

Численные значения в выражение передаточной функции следующие:

K = 100 град / (В∙с); kдс = 0,01 В / (град∙с); Tу = 0,01 с; Tм = 0,1с.

Далее запишем характеристический многочлен замкнутой системы

заменив s на : (4)

Решение на Python

Здесь следует отметить, что подобные задачи на Python ещё никто не решал, во всяком случае я не нашёл. Это было связано с ограниченными возможностями работы с комплексными числами. С появлением SymPy можно сделать следующее:

Где I мнимая единица, w- круговая частота, T1= Tу = 0.01 ,T2= Tм = 0.1 Получим развёрнутое выражение для многочлена:

Характеристический многочлен замкнутой системы – -I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1

Сразу видим, что многочлен третьей степени. Теперь получим мнимую и действительную части в символьном отображении:

Действительная часть Re= -T1*w**2 — T2*w**2 + 1 Мнимая часть Im= -T1*T2*w**3 + w

Сразу видим вторую степень действительной части и третью мнимой. Подготовим данные для построения годографа Михайлова. Введём численные значения для T1 и T2, и будем менять частоту от 0 до 100 с шагом 0.1 и построим график:

Из графика не видно, то годограф начинается на действительной положительной оси. Нужно изменить масштабы осей. Приведу полный листинг программы:

Характеристический многочлен замкнутой системы — -I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1 Действительная часть Re= -T1*w**2 — T2*w**2 + 1 Мнимая часть Im= -T1*T2*w**3 + w

Теперь уже видно, что годограф начинается на действительной положительной оси. САУ устойчива, n=3, годограф совпадает с приведённым на первом рисунке.

Дополнительно убедится в том, что годограф начинается на действительной оси можно дополнив программу следующим кодом для w=0:

Начальная точка М(1,0)

САУ сварочного робота

Рисунок 3. Структурная схема САУ позиционированием НСУ

Характеристическое уравнение данной САУ будет иметь вид :

где K – варьируемый коэффициент усиления системы, a – определённая положительная константа. Численные значения: K = 40; a = 0,525.

Далее путём замены s на , получим функцию Михайлова: (5)

Решение на Python

Характеристический многочлен замкнутой системы — w**4 — 6*I*w**3 — 11*w**2 + 46*I*w + 21 Начальная точка М(21,0) Действительная часть Re= w**4 — 11*w**2 + 21 Мнимая часть Im= -6*w**3 + 46*w

Построенный годограф Михайлова, начинаясь на вещественной положительной оси (М (21,0)), огибает в положительном направлении начало координат, проходя последовательно четыре квадранта, что соответствует порядку характеристического уравнения. Значит, данная САУ позиционированием НСУ – устойчива.

Выводы

При помощи модуля SymPy Python получен простой и наглядный инструмент для решения задач расчёта устойчивости систем автоматического управления, что является обязательным условием работоспособности любого промышленного робота и манипулятора.

Применение диаграммы Михайлова

Диаграмма Михайлова – это графическое представление векторных отношений, которое помогает анализировать движение точки в комплексной плоскости. Эта диаграмма часто используется в физике при изучении кинематики, электродинамики, теории управления и других дисциплинах.

Применение диаграммы Михайлова позволяет:

• Анализировать и предсказывать движение точки с заданными параметрами;
• Определять зависимости между векторами скорости и ускорения;
• Оптимизировать процесс настройки системы управления;
• Оценивать характеристики системы и определять ее устойчивость.

Диаграмма Михайлова представляет собой графическое изображение векторной диаграммы, где вектора скорости и ускорения представлены в виде отрезков на комплексной плоскости. Построение диаграммы осуществляется с помощью пошаговых действий:

1. Выбрать масштаб для осей координат, так чтобы точка начала осей соответствовала начальному положению точки;
2. Точку начала отложить на плоскости и обозначить ее символом «O»;
3. Отложить вектор скорости от точки «O» и обозначить его символом «V»;
4. Отложить вектор ускорения от конца вектора скорости и обозначить его символом «A»;
5. Повторить шаги 3 и 4 несколько раз, если необходимо, чтобы построить траекторию движения;
6. Определить значения векторов скорости и ускорения;
7. Провести соответствующие графические построения для анализа системы.

Применение диаграммы Михайлова позволяет визуализировать сложные векторные отношения и сделать выводы о движении системы. Эта методика широко используется в инженерии и физике для расчета и анализа систем управления, оптимизации процессов и изучения физических закономерностей.

Построение графика работы

Для построения графика работы необходимо следовать следующим шагам:

1. Определить время работы: установите начальное и конечное время работы.
2. Разделить время на периоды: если работа имеет несколько этапов или фаз, определите их и разделите время на соответствующие периоды.
3. Выбрать масштаб графика: определите период времени, который будет отображаться на оси X (горизонтальной оси) графика. Выберите такой масштаб, чтобы было удобно воспринимать информацию.
4. Определить шаг по времени: решите, в каких отрезках времени вы будете отображать информацию о выполнении работ или этапов. Например, каждый час, каждый день и т.д.
5. Создать таблицу данных: создайте таблицу, в которой будет представлена информация о выполнении работ или этапов в заданные моменты времени.
6. Заполнить таблицу данными: внесите в таблицу информацию о выполнении работ или этапов в различные моменты времени с учетом шага по времени.
7. Отобразить данные на графике: используйте таблицу данных для отображения информации на графике работы. Нанесите на график отметки для каждой фазы или этапа работы в соответствии с их продолжительностью в заданные моменты времени.
8. Построить график работы: постройте график работы, используя полученные данные. Отобразите ось X для времени и ось Y для фаз или этапов работы. Нанесите на график отметки для каждой фазы или этапа работы в соответствии с их продолжительностью в заданные моменты времени.

Следуя этим шагам, вы сможете построить график работы, который поможет наглядно представить выполнение работ или этапов в заданные моменты времени.