Термодинамические уравнения состояния
Термодинамические уравнения состояния – это математические выражения, которые описывают связь между различными термодинамическими параметрами состояния системы. Они позволяют нам выразить один параметр через другие и понять, как изменение одного параметра влияет на другие.
Уравнение состояния идеального газа
Одним из наиболее простых и широко используемых термодинамических уравнений состояния является уравнение состояния идеального газа. Оно описывает связь между давлением (P), объемом (V) и температурой (T) идеального газа.
Уравнение состояния идеального газа можно записать следующим образом:
PV = nRT
где P – давление газа, V – объем газа, n – количество вещества газа (в молях), R – универсальная газовая постоянная, T – температура газа в абсолютной шкале (Кельвин).
Это уравнение позволяет нам выразить любой из параметров (P, V, T) через другие, если известны значения остальных параметров и универсальная газовая постоянная. Например, мы можем выразить давление газа через объем и температуру, или объем через давление и температуру.
Уравнение состояния Ван-дер-Ваальса
Уравнение состояния Ван-дер-Ваальса является модификацией уравнения состояния идеального газа и учитывает некоторые реальные свойства газов, такие как объем молекул и их взаимодействие.
Уравнение состояния Ван-дер-Ваальса записывается следующим образом:
(P + a/V^2)(V – b) = RT
где P – давление газа, V – объем газа, a и b – константы, зависящие от свойств газа, R – универсальная газовая постоянная, T – температура газа в абсолютной шкале.
Уравнение состояния Ван-дер-Ваальса учитывает объем молекул газа (параметр b) и силы взаимодействия между молекулами (параметр a). Это позволяет более точно описывать поведение реальных газов, особенно при высоких давлениях и низких температурах.
Другие уравнения состояния
В дополнение к уравнениям состояния идеального газа и Ван-дер-Ваальса, существует множество других уравнений состояния, которые описывают поведение различных веществ и состояний вещества.
Некоторые из наиболее известных уравнений состояния включают уравнение состояния Клапейрона-Менделеева, уравнение состояния Редлиха-Квонга и уравнение состояния Пенга-Робинсона. Каждое из этих уравнений имеет свои особенности и применяется в различных областях физики и химии.
В целом, термодинамические уравнения состояния играют важную роль в описании и предсказании поведения систем в различных условиях. Они позволяют нам понять, как изменение одного параметра влияет на другие и как система реагирует на внешние воздействия.
Второе начало для равновесных процессов
Равновесные состояния адиабатического процесса $\delta Q=0$ для идеального газа на плоскости $(P,V)$
находятся на кривой $P\,V^\gamma=\text{const}$. Поэтому из данного состояния
при помощи только одной адиабаты нельзя попасть в произвольное состояние (в произвольную точку на $(P,V)$ плоскости).
Это утверждение, называемое принципом адиабатической недостижимости
Каратеодори, справедливо для любой термодинамической системы.
Следствием «принципа недостижимости» является то, что
изотермы и адиабаты на плоскости $(P,V)$ могут пересекаться не более, чем в одной точке.
Это несложно доказать, пользуясь вторым началом термодинамики, в форме запрета вечного двигателя второго рода:
Система не может в замкнутом цикле выполнять работу, получая тепловую энергию
только от одного термостата.
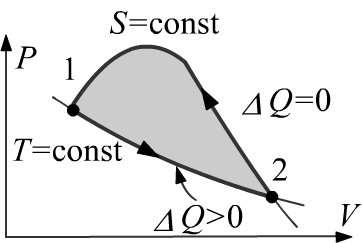
Действительно, пусть изотермический процесс соединяет два состояния
(точки $1$ и $2$). В этом процессе система получает от термостата
тепло $\Delta Q ~=~ (U_2-U_1) + \Delta A \gt 0$.
Допустим, что возможен обратный (из точки $2$ в точку $1$)
адиабатический процесс для которого $\Delta Q=0= (U_1-U_2) + \Delta \tilde{A}$.
Складывая эти два соотношения, получаем $\Delta A+\Delta \tilde{A} \gt 0$.
Это означает, что в таком замкнутом цикле система производит работу,
что противоречит второму началу.
Каждая изотерма соответствует определённой температуре $T$,
которая её «нумерует». Эти изотермы не пересекаются (они соответствуют различным термостатам)
и непрерывно заполняют плоскость $(P,V)$.
Точно также принцип адиабатической недостижимости означает,
что адиабаты непересекаясь, заполняют всю плоскость состояний.
Соответственно, можно ввести переменную состояния, которая нумерует адиабаты.
Эту переменную и называют энтропией.
Изобарный процесс
Рисунок 2. Изобарный процесс . Автор24 — интернет-биржа студенческих работ
Определение 1
Изобарный процесс – это такой термодинамический процесс, который может протекать при постоянном давлении. Подобный процесс осуществляется, например, когда помещается газ в плотный цилиндр, где есть подвижный поршневой крючок.
На поршень действует постоянная внешняя сила. Она достигается при подводе или отводе теплоты к объекту. При этом сама подвижная часть поршня способна менять свое местоположение при изменении параметров температуры. От этого зависит направление движения поршня. Согласно закону Гей-Люссака, объем газа в нем меняется, исходя из уравнения закона. Из этого следует, что занимаемый объем газа может быть прямо пропорционален определенной температуре воздействия. Внутренняя энергия газов изменяется под действием температурного режима извне. Этим правилом характеризуется весь изобарный процесс в термодинамике.
Принципы действия тепловых машин
Тепловым двигателем называют устройство, преобразующее внутреннюю энергию топлива в механическую энергию.
Основные части теплового двигателя:
- Нагреватель – тело с постоянной температурой, преобразующее внутреннюю энергию топлива в энергию газа. В каждом цикле работы двигателя нагреватель передает рабочему телу некоторое количество теплоты.
- Рабочее тело – это газ, совершающий работу при расширении.
- Холодильник – тело с постоянной температурой, которому рабочее тело передает часть тепла.
Любая тепловая машина получает от нагревателя некоторое количество теплоты \( Q_1 \) и передает холодильнику количество теплоты \( Q_2 \). Так как \( Q_1 > Q_2 \), то совершается работа \( A’ = Q_1 – Q_2 \).
Тепловой двигатель должен работать циклически, поэтому расширение рабочего тела должно сменяться его сжатием. Работа расширения газа должна быть больше работы сжатия, совершаемой внешними силами (условие совершения полезной работы). Температура газа при расширении должна быть выше, чем температура при сжатии. Тогда давление газа во всех промежуточных состояниях при сжатии будет меньше, чем при расширении.
В реальных тепловых машинах нагревателем является камера сгорания. В них рабочее тело нагревается за счет тепла, выделяющегося при сгорании топлива. Количество теплоты, выделяющееся при сгорании топлива, вычисляется по формуле:
где \( q \) – удельная теплота сгорания топлива, \( m \) – масса топлива.
Холодильником чаще всего у реальных двигателей служит атмосфера.
Виды тепловых двигателей:
- паровой двигатель;
- турбина (паровая, газовая);
- двигатель внутреннего сгорания (карбюраторный, дизельный);
- реактивный двигатель.
Тепловые двигатели широко используются на всех видах транспорта: на автомобилях – двигатели внутреннего сгорания; на железнодорожном транспорте – дизельные двигатели (на тепловозах); на водном транспорте – турбины; в авиации – турбореактивные и реактивные двигатели. На тепловых и атомных электростанциях тепловые двигатели приводят в движение роторы генераторов переменного тока.
Первое начало термодинамики

Любая замкнутая система характеризуется своей внутренней энергией $U$.
Внутренняя энергия увеличивается при получении тепловой энергии $\delta Q$
и уменьшается при совершении системой работы $\delta A=P\,dV$:
$$
dU ~=~\delta Q ~-~\delta A.~~~~~~~~~~~~~
$$
Тепловая энергия поступает ($\delta Q \gt 0$) в систему при её контакте с более горячим телом
или покидает ($\delta Q \lt 0$) систему при контакте с более холодным телом (если $\delta A=0$).
Работа $\delta A= P\,dV$, выполненная системой при расширении газа,
уменьшает внутреннюю энергию (если $\delta Q=0$).
При сжатии газа ($\delta A \lt 0$) внутренняя энергия увеличивается
(для этого необходимо затратить работу со стороны внешних сил).
Закон сохранения энергии, записанный в такой форме, называют первым началом термодинамики.
Он имеет очень широкую область применимости
и справедлив для любой системы находящейся, как в равновесии, так и вдали от него.
Микроскопические и макроскопические параметры
Микроскопическое состояние (или микросостояние) — это состояние системы, определяемое заданием координат и импульсов всех составляющих систему частиц.
Макроскопическое состояние (или макросостояние) — это состояние системы, характеризуемое небольшим числом величин (Р, V, T) и, быть
может, еще некоторыми другими).
Величины, характеризующие макросостояние, называются макроскопическими параметрами. Те из них, которые характеризуют внутреннее
состояние системы, называются внутренними параметрами, а те, которые описывают внешнюю среду (внешние тела, поля), — внешними параметрами.
Смысл разделения на микро- и макросостояния состоит в следующем. Хаотическая динамика на микроскопическом уровне (молекулярный
хаос) проявляется как упорядоченное изменение состояния на макроскопическом уровне. Точное описание поведения системы на языке
микросостояний чрезвычайно сложно, если вообще возможно. Вместе с тем достаточно полное описание макроскопического поведения системы большого числа частиц может быть получено с помощью небольшого числа макроскопических параметров — давления Р, температуры Т, объема V и, быть может, еще нескольких других существенных характеристик. Если не интересоваться внутренним строением вещества, то достаточно ограничиться описанием на уровне макросостояния. При необходимости можно уточнить это описание, вводя в рассмотрение те или иные дополнительные параметры (например, те из них, которые характеризуют форму тела, его заряд, магнитный момент и т. д.).
Циклические процессы
В термодинамике и практических приложениях важную роль играют замкнутые циклы, состоящие из
равновесных процессов. Изменяясь в этих процессах, система периодически возвращается в исходное состояние.
Напомним, что, если $Q\gt 0$, то тепловая энергия получается системой,
а при $Q\lt 0$ — отдаётся наружу. Положительная работа $\delta A~=~P\,dV$
означает, что её производит система (а не «мы»),
а если $A \lt 0$ — работа совершается над системой, т.е. «нами».
Для замкнутого цикла $\Delta U = 0$ (возвращаемся в тоже состояние), поэтому $A=Q$, где:
$$
A ~=~ \oint P\,dV,~~~~~~~~~~~~~~~~=~~~~~~~~~~~~~~~Q~=~\oint T\,dS.
$$
Если обход контура равновесного процесса производится по часовой стрелке (см. стрелки на рисунках),
то выполняемая системой работа $A$ на плоскости $(P,V)$ равна площади, окружаемой кривой цикла,
а получаемая системой теплота $Q$ — площади для этого же процесса на плоскости $(T,S)$.

Действительно, интеграл от $P\,dV$ по верхней кривой между точками $(1-2)$
положителен и равен площади под этой кривой. Движение в обратную сторону
$(2-1)$ по нижней кривой приводит к «отрицательной площади» под этой кривой.
Сумма этих площадей равна площади закрашенной области. Аналогично для плоскости $(T,S)$.
Если направление контура меняется на противоположный, то меняются и знаки.
Тепло система отдаёт $Q\lt 0$,
и чтобы такой цикл был возможен, необходимо затрачивать «внешнюю» работу: $A = Q\lt 0$.
В силу того, что энтропия $dS=\delta Q/T$ является переменной состояния,
интеграл от неё по замкнутой кривой, как и для внутренней энергии,
равен нулю:
$$
\oint \frac{\delta Q}{T}~=~0.
$$
Это соотношение называют вторым началом термодинамики для равновесных процессов.
Термодинамическая система
Системой называется совокупность рассматриваемых тел (частиц), которые могут взаимодействовать между собой и с другими телами (внешней средой) посредством обмена веществом и энергией. В термодинамике рассматриваются большие системы, называемые термодинамическими системами. Примером термодинамической системы может служить газ, в 1 см³ которого при нормальных условиях содержится n_Л — 2,687e19 молекул (число Лошмидта). Система, не обменивающаяся веществом и энергией с окружающей средой, называется
изолированной (или замкнутой) системой.
Система, обменивающаяся с внешней средой только энергией (но не массой), называется закрытой системой.
Система, обменивающаяся с внешней средой веществом и энергией, называется открытой системой.
Первый закон термодинамики
Закон сохранения и превращения энергии, распространенный на тепловые явления, называется первым законом (началом) термодинамики.
Можно дать формулировку этого закона исходя из способов изменения внутренней энергии.
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
Если рассматривать работу самой системы над внешними телами, то закон может быть сформулирован так:
количество теплоты, переданное системе, идет на изменение ее внутренней энергии и совершение системой работы над внешними телами:
Если система изолирована и над ней не совершается работа и нет теплообмена с внешними телами, то в этом случае внутренняя энергия не изменяется. Если к системе не поступает теплота, то работа системой может совершаться только за счет уменьшения внутренней энергии. Это значит, что невозможно создать вечный двигатель – устройство, способное совершать работу без каких-либо затрат топлива.
Первый закон термодинамики для изопроцессов
Изотермический процесс: \( Q=A’\,(T=const, \Delta U=0) \)Физический смысл: все переданное газу тепло идет на совершение работы.
Изобарный процесс: \( Q=\Delta U+A’ \)Физический смысл: подводимое к газу тепло идет на увеличение его внутренней энергии и на совершение газом работы.
Изохорный процесс: \( Q=\Delta U\,(V=const, A’=0) \)Физический смысл: внутренняя энергия газа увеличивается за счет подводимого тепла.
Адиабатный процесс: \( \Delta U=-A’ \) или \( A=\Delta U\,\mathbf{(Q=0)} \)Физический смысл: внутренняя энергия газа уменьшается за счет совершения газом работы. Температура газа при этом понижается.
Задачи об изменении внутренней энергии тел
Такие задачи можно разделить на группы:
- При взаимодействии тел изменяется их внутренняя энергия без совершения работы над внешней средой.
- Рассматриваются явления, связанные с превращением одного вида энергии в другой при взаимодействии двух тел. В результате происходит изменение внутренней энергии одного тела вследствие совершенной им или над ним работы.
При решении задач первой группы:
- установить, у каких тел внутренняя энергия уменьшается, а у каких – возрастает;
- составить уравнение теплового баланса \( (\Delta U=0) \), при записи которого в выражении \( Q =cm(t_2 – t_1) \) для изменения внутренней энергии нужно вычитать из конечной температуры тела начальную и суммировать члены с учетом получающегося знака;
- решить полученное уравнение относительно искомой величины;
- проверить решение.
При решении задач второй группы:
- убедиться, что в процессе взаимодействия тел теплота извне к ним не подводится, т.е. действительно ли \( Q = 0 \);
- установить, у какого из двух взаимодействующих тел изменяется внутренняя энергия и что является причиной этого изменения – работа, совершенная самим телом, или работа, совершенная над телом;
- записать уравнение \( Q = \Delta U + A \) для тела, у которого изменяется внутренняя энергия, учитывая знак перед работой и КПД рассматриваемого процесса;
- если работа совершается за счет уменьшения внутренней энергии одного из тел, то \( А= -\Delta U \), а если внутренняя энергия тела увеличивается за счет работы, совершенной над телом, то \( A=\Delta U \);
- найти выражения для \( \Delta U \) и \( A \);
- подставить в исходное уравнение вместо \( \Delta U \) и \( A \) выражения для них, получить окончательное соотношение для определения искомой величины;
- решить полученное уравнение относительно искомой величины;
- проверить решение.
Равновесное состояние — термодинамическая система
Равновесное состояние термодинамической системы ( тела) зависит от внешних условий и температуры.
|
Различные типы равновесий механической системы. кривые показывают траектории центра масс при вращении тела вокруг ребра в плоскости основания. 1 — стабильное, 2 — лабильное, 3 — метастабильное. |
Равновесное состояние термодинамической системы называют устойчивым ( стабильным), если любое бесконечно малое воздействие на нее вызывает бесконечно малое изменение состояния, а при устранении этого воздействия система возвращается в исходное состояние. Если при бесконечно малом воздействии происходит конечное изменение состояния — это неустойчивое ( лабильное) равновесие. Для термодинамических систем неустойчивость равновесия означает его отсутствие, так как малые вариации состояний таких систем происходят самопроизвольно в связи с флюктуациями физических параметров.
Равновесное состояние термодинамической системы должно определяться совокупностью внешних и внутренних параметров. Если система переходит из одного состояния в другое, то в процессе перехода изменяются как внешние параметры, характеризующие окружающую среду, так и внутренние, характеризующие изучаемую систему. Для характеристики конкретных условий, в которых находится данная система ( вещество), или процесса, идущего в системе, необходимо прежде всего знать такие распространенные внутренние параметры, как абсолютное давление, абсолютная температура, удельный объем или плотность.
Равновесное состояние термодинамической системы, а следовательно, и макроскопические свойства системы в состоянии равновесия вполне определяются ее внешними параметрами и температурой.
Равновесное состояние термодинамической системы характеризуется при постоянных внешних условиях неизменностью параметров во времени и отсутствием в системе потоков, или, другими словами, отсутствием стремления к самопроизвольному изменению состояния.
Равновесным состоянием термодинамической системы называется такое состояние, которое не изменяется со временем, причем эта неизменность параметров не обусловлена какими-либо внешними относительно данной системы процессами. В рассмотренном примере с распределением температуры вдоль стержня такими процессами были процессы кипения воды и таяния льда.
Равновесным состоянием термодинамической системы называется такое состояние, которое не изменяется во времени. Отметим, что неизменность параметров в состоянии равновесия не обусловлена каким-либо внешним воздействием или процессом.
Этот метод отыскания равновесного состояния термодинамической системы аналогичен методу возможных перемещений в теоретической механике.
|
Изменение концентрации твердого раствора на основе паяемого материала Л и припоя В на границе со швом при температуре пайки.| Изменение функции состояния Ф при переходе системы в более равновесное состояние D. А — метастабильное состояние. В — лабильное состояние. |
Следовательно, переход из одного стабильного или метастабильного равновесного состояния термодинамической системы в другое проходит ( обратимо или необратимо) две стадии: стадию активируемого состояния и стадию самопроизвольного неактнви-руемого изменения состояния.
Важное значение имеет утверждение термодинамики о том, что равновесное состояние термодинамической системы, а следовательно, и значения макроскопических свойств системы в состоянии равновесия вполне определяются ее внешними параметрами и температурой.
Уравнение (1.9) в пространстве отображает поверхность, которая характеризует всевозможные равновесные состояния химически однородной термодинамической системы.
Равновесным ( квазиравновесным, квазистатическим) называется процесс, состоящий из непрерывной последовательности равновесных состояний термодинамической системы.
Равновесным ( квазиравновесным, квазистатическим) называется процесс, состоящий из непрерывной последовательности равновесных состояний термодинамической системы. Строго говоря, каждое состояние, в котором пребывает система при протекании такого процесса, хотя и бесконечно мало, но отличается от равновесного, иначе сам процесс был бы невозможен. Для осуществления равновесного процесса параметры внешней среды должны изменяться бесконечно медленно. Реальный процесс можно считать равновесным, если характерное время изменения внешних параметров ( например, объема системы, температуры внешней среды) велико по сравнению с характерным временем установления равновесия в самой термодинамической системе — временем релаксации.
ПАРАМЕТРЫ СОСТОЯНИЯ
Физический энциклопедический словарь. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1983 .
(термодинамическиепараметры) — физ. величины, характеризующие равновесное состояние термодинамич.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .
Смотреть что такое «ПАРАМЕТРЫ СОСТОЯНИЯ» в других словарях:
параметры состояния — — Тематики энергетика в целом EN variables of state … Справочник технического переводчика
параметры состояния — 3.4.2 параметры состояния газа: Величины, характеризующие состояние газа. Примечание В настоящем стандарте в качестве параметров состояния газа приняты давление и температура газа. Источник … Словарь-справочник терминов нормативно-технической документации
параметры состояния — būsenos parametrai statusas T sritis chemija apibrėžtis Termodinaminę sistemą ir jos ryšį su aplinka nusakantys dydžiai. atitikmenys: angl. state parameters rus. параметры состояния … Chemijos terminų aiškinamasis žodynas
ПАРАМЕТРЫ СОСТОЯНИЯ ЭКОСИСТЕМЫ — наиболее общие (интегральные) информативные показатели функционирования экосистемы, позволяющие оценить ее состояние, степень отклонения от нормы. Экологический словарь, 2001 Параметры состояния экосистемы наиболее общие (интегральные)… … Экологический словарь
параметры состояния газа — 3.1 параметры состояния газа: Величины, характеризующие состояниегаза. Примечание В настоящем документе в качестве параметров состояния газа приняты давление и температура газа. Источник … Словарь-справочник терминов нормативно-технической документации
параметры состояния свободного нефтяного газа — 3.6 параметры состояния свободного нефтяного газа: Физические величины: температура, плотность и давление Источник … Словарь-справочник терминов нормативно-технической документации
ПАРАМЕТРЫ СОСТОЯНИЯ — (от греч. parametron отмеривающий, соразмеряющий) (термодинамич. параметры, термодинамич. переменные), физ. величины, характеризующие состояние термодинамич. системы в условиях термодинамического равновесия. Различают экстенсивные П. с.… … Химическая энциклопедия
Переменные состояния
Любая функция переменных состояния $f(P,V)$ является переменной состояния.
Интегрирование её дифференциала
$$
df(P,V) ~=~ \frac{\partial f}{\partial P}\,dP + \frac{\partial f}{\partial V}\,dV,~~~~~~~~~~~~~~~~
\frac{\partial^2 f}{\partial P\,\partial V}~=~\frac{\partial^2 f}{\partial V\,\partial P},~~~~~~~~~~~~~~~~
\int\limits^2_1 df(P,V) = f(P_2,\,V_2)-f(P_1,\,V_1).
$$
не зависит от пути на плоскости $(P,V)$ и определяется только начальной и конечной точкой.
Например поэтому $\Theta=P\,V/N$ или $U=P\,V/(\gamma-1)$ являются переменными состояния,
т.е. характеризуют текущее состояние системы, независимо от того, как она в него попала.
В термодинамике величины могут зависеть от различных переменных состояния.
Поэтому при записи частных производных принято указывать какие величины при дифференцировании постоянны.
Например, следующие производные в общем случае между собой не совпадают:
$$
\left(\frac{\partial U}{\partial P}\right)_{VN} ~\equiv~ \frac{\partial U(P,V,N)}{\partial P},~~~~~~~~~~~~~~~~
\left(\frac{\partial U}{\partial P}\right)_{TN} ~\equiv~ \frac{\partial U(P,T,N)}{\partial P}.
$$
Так, для идеального газа $U=N\,k\,T/(\gamma-1)=P\,V/(\gamma-1)$,
первая производная равна $V/(\gamma-1)$, а вторая — нулю.
Работа $A$ и теплота $Q$ не являются переменными состояния так как
они зависят от способа перехода в данное состояние.
Для работы $\delta A~=~P\,dV$, выполняемой газом, это очевидно, т.к. её значение на плоскости $(P,V)$
равно интегралу от $P(V)\,dV$ (площадь). Начальная и конечная точки
(состояния системы) могут быть соединены разными кривыми (процессами),
чему будет соответствовать различная работа. Так как $\delta Q = dU + \delta A$,
то и получаемая или отдаваемая системой теплота также зависит от характера процесса.
Поэтому говорить о накопленных телом в данном состоянии работе или теплоты («теплород»)
бессмысленно.
Принято использовать обозначение $df$ для бесконечно малых величин,
которые являются полными дифференциалами (и переменными состояния) и обозначение
$\delta g$ для малых величин не являющихся полным дифференциалом (таковы работа и теплота).
Все переменные состояния делятся на два класса относительно их поведения при мысленном разделении
пространственно-однородной системы на части.
Для аддитивных переменных $F_{общ}~=~F_1+F_2$.
Для неаддитивных: $f_{общ}~=~f_1~=~f_2$.
Аддитивные переменные состояния пропорциональны
числу молекул при их фиксированной концентрации $n=N/V$ или их удельном объёме $v=V/N$
(объём на одну молекулу).
Примерами таких переменных являются объём $V$, число частиц $N$ и внутренняя энергия $U$.
В переменных $(T,V)$ для аддитивных переменных выполняется следующее соотношение:
$$
F(T,V,N) ~=~ N\cdot f(T,\,V/N).
$$
Давление $P$ и температура $T$ — это неаддитивные
переменные состояния (их также называют «интенсивными»).
Они не зависят явно от числа молекул и других аддитивных переменных (зависят только от неаддитивных):
$$
F(T,V,N) ~=~ f(T,\,V/N).
$$
Например, давление идеального газа $P~=~k\,T\,(N/V)~=~k\,T\,n$ не зависит от числа молекул
(только от их концентрации $n$).
В тоже время
аддитивная внутренняя энергия явным образом пропорциональна числу молекул: $U~=~N\,kT/(\gamma-1)$.
Любые удельные величины в расчёте на одну частицу — неаддитивны (удельный объём $v=V/N$,
удельная энергия $u=U/N$, удельная теплоёмкость $c=C/N$, см. ниже, и т.д.).
Естественно, вместо переменных $(T,V,N)$ можно использовать другие, например $(P,U,N)$.
Тогда, например, для аддитивных величин будет: $F(P,U,N)=N\,f(P,\,U/N)$.
Переменные состояния обычно вычисляются в статистическом предельном переходе:
$$
N\to \infty,~~~~~~~~~V\,=\,v\,N,~~~~~~~~v=\frac{1}{n}=\text{const}.
$$
Термодинамическое состояние системы в таком пределе не зависит от свойств поверхности сосуда и его формы).
Действительно, пусть $L$ — линейные
размеры сосуда и $V\sim L^3$. Число молекул у стенок в слое шириной $D \ll L$
по порядку
равно $n\,D\,L^2\lt\sim n L^2 \sim (n\,V)^{2/3}\sim N^{2/3}$. Отношение
числа молекул «чувствующих» свойства поверхности к их общему числу $\sim N^{2/3}/N=N^{-1/3} \ll 1$.
Объём сложной формы всегда можно разбить на макроскопические объёмы простой формы,
имеющие в пределе $N\to\infty$ одинаковые параметры состояния.
3 Основные параметры состояния
Давление (Р) — физическая величина, характеризующая интенсивность нормальных сил, с которыми одно тело действует на поверхность другого. Единицей измерения давления является Паскаль (Па).
Давление подразделяется на абсолютное Р, атмосферное Рa, избыточное Ри, вакуум РB (см. рисунок 1)
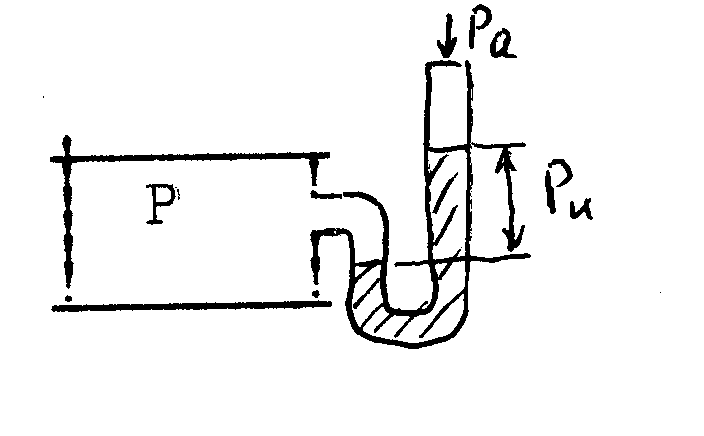
Рисунок 1 – Соотношение давлений
Температура (Т) характеризует степень нагретости тела, связанную с кинетической энергией частиц рабочего тела. Чем ниже температура, тем меньше кинетическая энергия. Значения температуры определяют по температурному изменению какого-либо удобного для измерения физического свойства вещества с помощью температурной шкалы.
Термодинамическая температурная шкала основана на втором начале термодинамики. Температура, при которой полностью прекращается тепловое движение молекул, принята за абсолютный нуль – начало отсчета. Другой точкой определяющей термодинамическую температурную шкалу, является температура тройной точки воды (температура равновесия между льдом, водой и паром), равная 273,16 К. За единицу измерения термодинамической температурной шкалы принят градус Кельвина (Т, К), равный 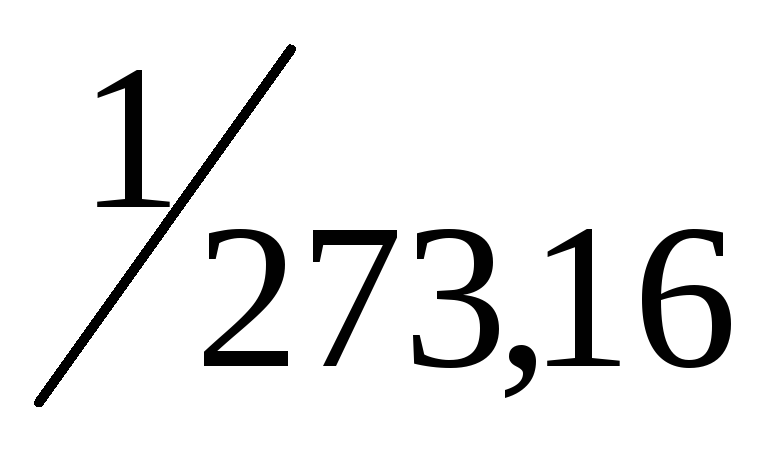 части интервала от абсолютного нуля до температуры тройной точки воды. Часто ту же температуру измеряют по шкале Цельсия (t, ºC).
части интервала от абсолютного нуля до температуры тройной точки воды. Часто ту же температуру измеряют по шкале Цельсия (t, ºC).
Объем (V) рабочего тела в измеряется в м 3 . Удельным объемом называется объем  , занимаемый единицей массы рабочего тела. Для однородного рабочего тела удельный объем
, занимаемый единицей массы рабочего тела. Для однородного рабочего тела удельный объем  = V/М, при нормальных условиях ( ºC, 101,325 кПа).
= V/М, при нормальных условиях ( ºC, 101,325 кПа).
Величина обратная  , является плотностью рабочего тела =1/
, является плотностью рабочего тела =1/ =MV. Следовательно, ·
=MV. Следовательно, · =1.
=1.
Иногда употребляют понятие удельного веса вещества. Под удельным весом понимают вес вещества в единице его объема. В соответствии со вторым законом Ньютона плотность и удельный вес связаны соотношением:
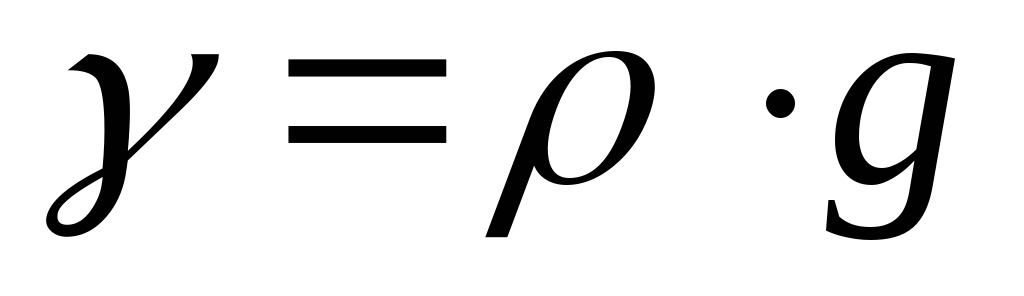 ,
,
где g – ускорение свободного падения, м/с 2 .
5 Уравнение состояние
Состояние ТДС может быть равновесным и неравновесным. Равновесное состояние изолированной ТДС характеризуется постоянством по всему объему, занимаемому системой, таких параметров, как Р (механическое равновесие) и Т (термическое равновесие).
В неизолированной системе равновесное состояние однозначно определяется внешними условиями, т.е. давлением и температурой внешней среды. В равновесных ТДС отсутствуют стационарные потоки, например, теплоты и вещества. Всякая изолированная система с течением времени приходит в равновесное состояние, которое остается затем неизменным, пока система не будет выведена из него внешним воздействием.
Уравнение состояние – уравнение выражающее связь между параметрами равновесного состояния ТДС. Математическая зависимость между тремя параметрами для состояния равновесия носит название термическое уравнение состояния. В общем виде оно выражается:
F(V,P,T,)=0 (1)
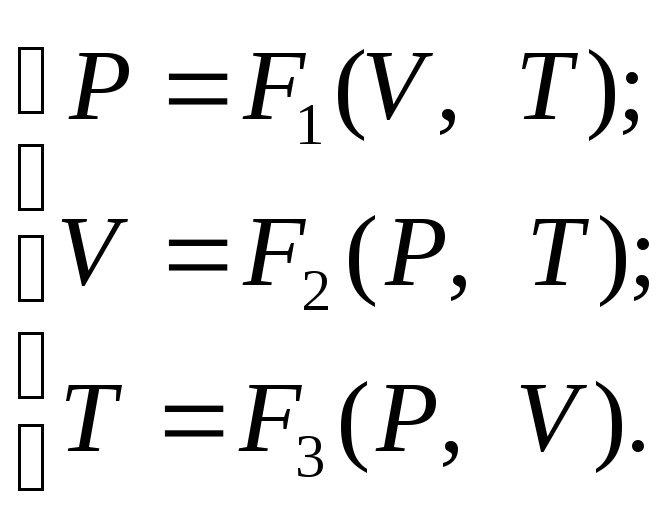 (2)
(2)
Продифференцировав эту систему уравнений по независимым переменным, получим приращение параметров:
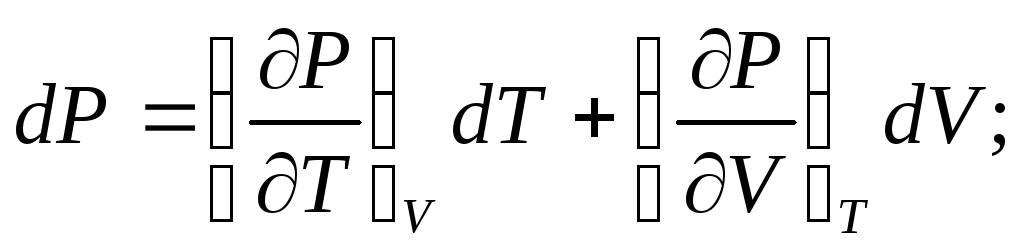
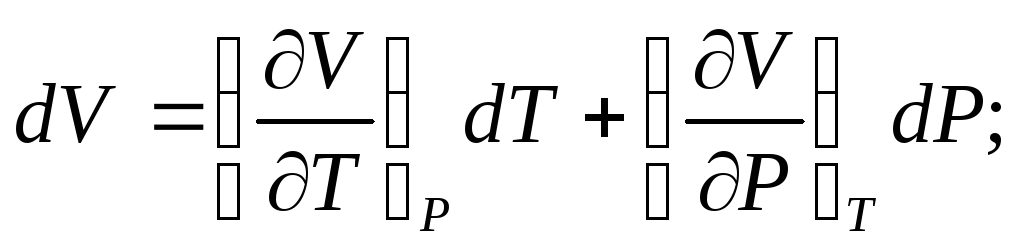 (3)
(3)
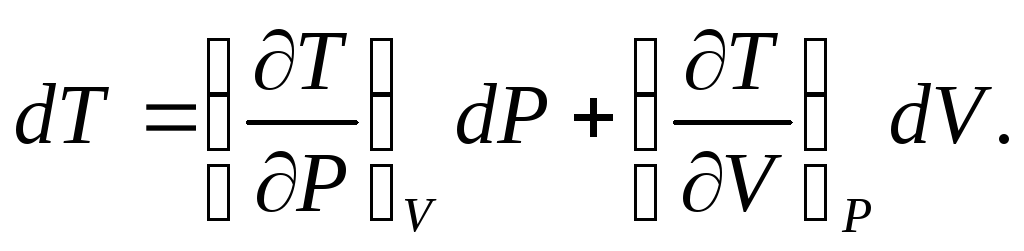
В индексе при частной производной указан постоянный параметр. Приняв условие dP=0, можно получить дифференциальное уравнение состояния:
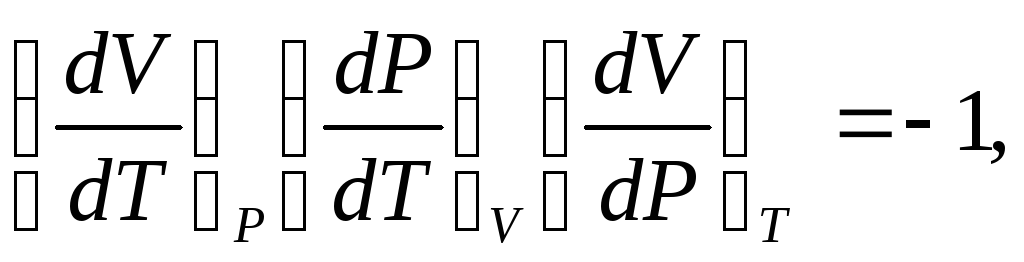 (4)
(4)
куда входят частные производные, имеющие определенный физический смысл – термические характеристики рабочего тела.
При расчетах обычно используются значения, получаемые путем деления 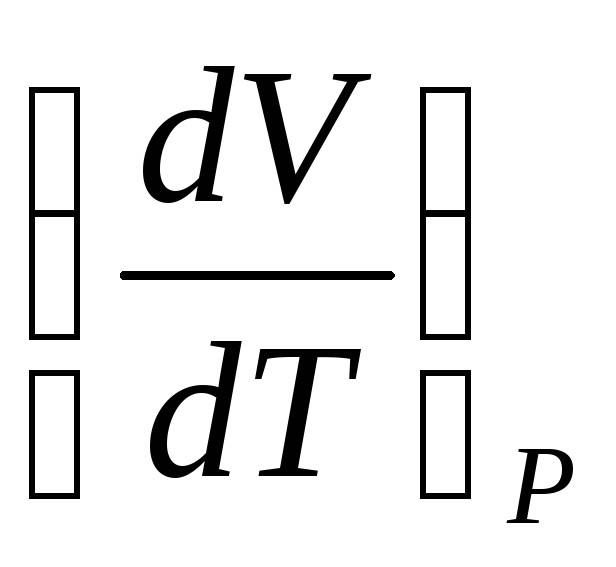 и
и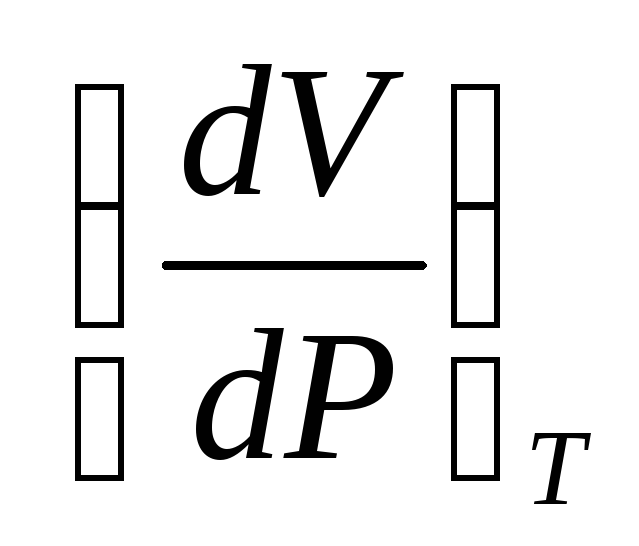 на удельный объем газа
на удельный объем газа  при
при 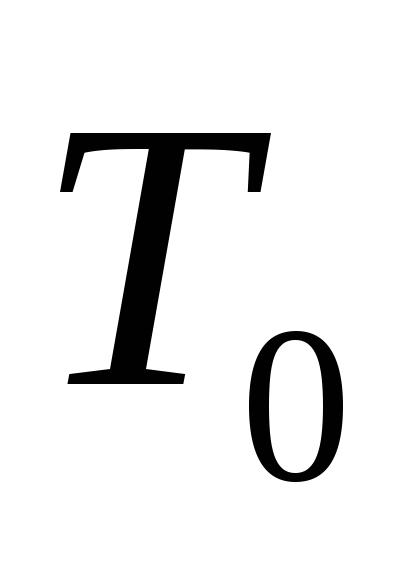 = 287 К и
= 287 К и 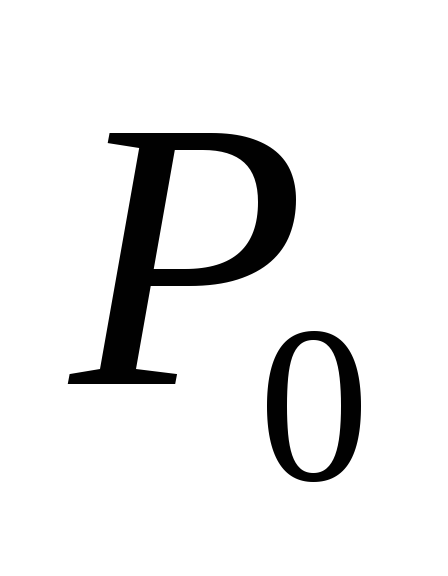 = 101,325 кПа или
= 101,325 кПа или 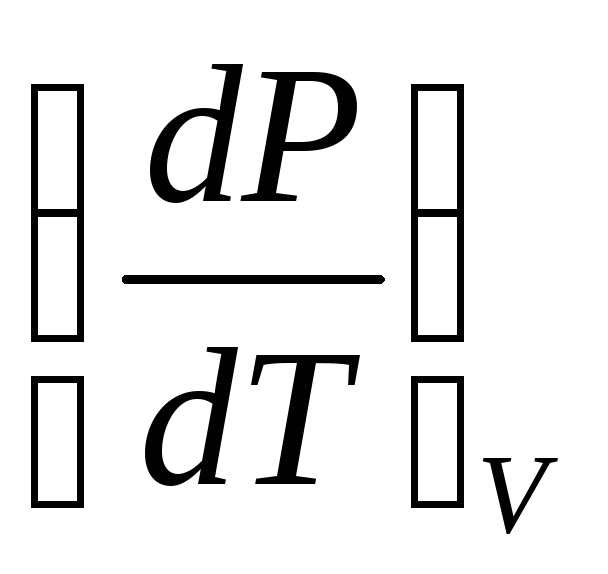 деленное на давление
деленное на давление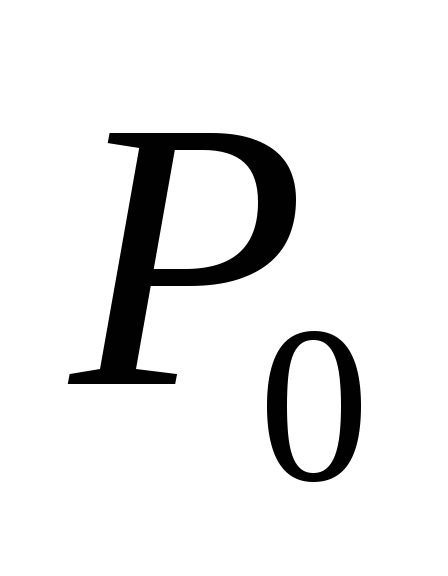 при тех же условиях:
при тех же условиях:
 , (5)
, (5)
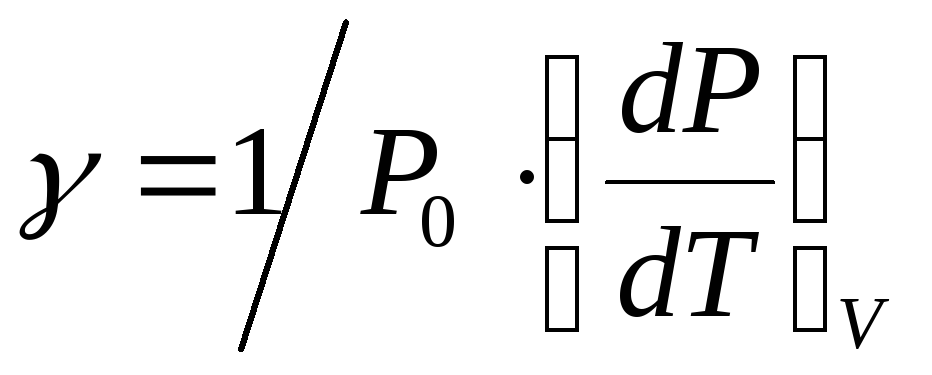 , (6)
, (6)
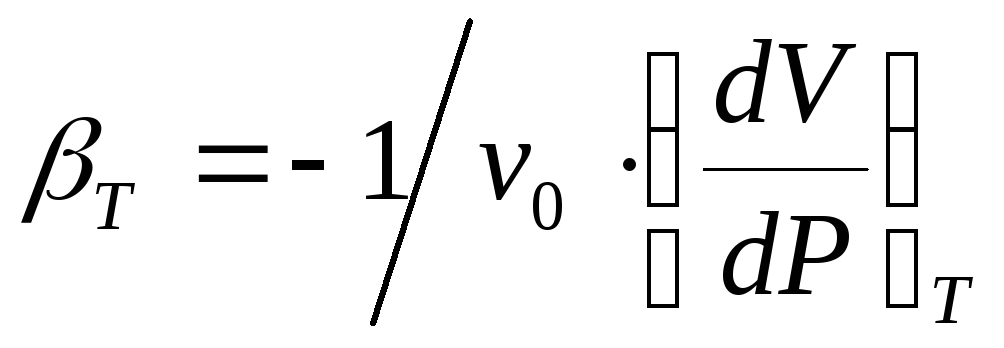 , (7)
, (7)
где  – коэффициент термического расширения;
– коэффициент термического расширения;
 –коэффициент термической упругости;
–коэффициент термической упругости;
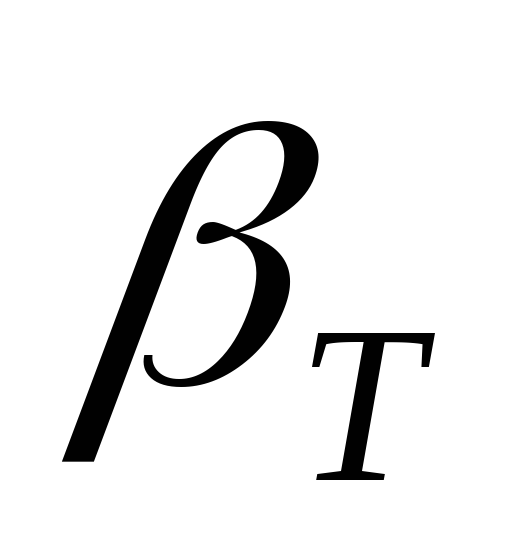 –коэффициент изотермической сжимаемости.
–коэффициент изотермической сжимаемости.
Подставив выражения (5), (6), (7) в уравнение (4) получим:
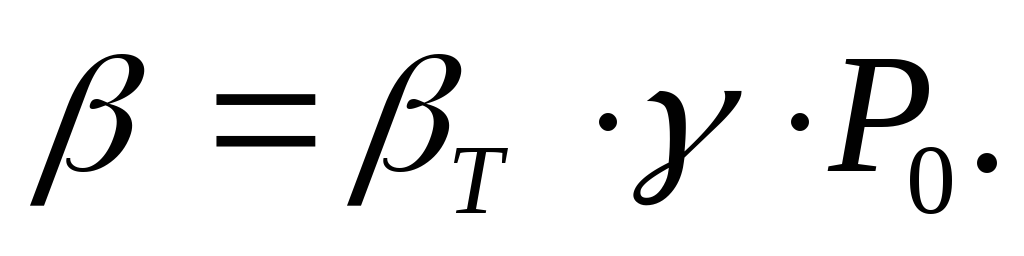 (8)
(8)
Так как соотношения (3-7) выведены на основе зависимостей (2), то выражение (8) справедливо для любых рабочих тел.
Количество теплоты. Удельная теплоемкость вещества
Количество теплоты – это скалярная физическая величина, равная энергии, которую тело получило или отдало при теплопередаче.
Обозначение – \( Q \), в СИ единица измерения – Дж.
Удельная теплоемкость – это скалярная физическая величина, численно равная количеству теплоты, которое тело массой 1 кг получает или отдает при изменении его температуры на 1 К.
Обозначение – \( c \), в СИ единица измерения – Дж/(кг·К).
Удельная теплоемкость определяется не только свойствами вещества, но и тем, в каком процессе осуществляется теплопередача. Поэтому выделяют удельную теплоемкость газа при постоянном давлении – \( c_P \) и удельную теплоемкость газа при постоянном объеме – \( c_V \). Для нагревания газа на 1 К при постоянном давлении требуется большее количество теплоты, чем при постоянном объеме – \( c_P > c_V \).
Формула для вычисления количества теплоты, которое получает тело при нагревании или отдает при охлаждении:
где \( m \) – масса тела, \( c \) – удельная теплоемкость, \( T_2 \) – конечная температура тела, \( T_1 \) – начальная температура тела.
Важно!
При решении задач на расчет количества теплоты при нагревании или охлаждении можно не переводить температуру в кельвины. Так как 1К=1°С, то\( \Delta T=\Delta t \)






























