История создания
Матлаб как язык программирования был создан в 1970-х годах неким Кливом Моулером, деканом факультета компьютерных наук в университете Нью-Мексико. В самой первой своей версии The Matlab не был полноценным языком. Он представлял собой простой интерактивный матричный калькулятор.
Соответствующий инструмент упрощал студентам использование таких библиотек как Linpack и EISPACK для Fortan. Он стал настоящим помощником тем, кто не умеет программировать. Получит стремительное распространение среди университетов США.
В 1980-х Клив Моулер познакомился с Джоном Литтлом, который подал идею – переделать The Matlab на C, а затем продавать получившийся пакет обладателям компьютеров IBM. Так появилась коммерческая компания The MathWorks, а также коммерческое распространение языка вместе с интегрированной средой.
Массивы:
Начнем с задания одномерных массивов:
Задание в командной строке: x = или x = Задание отдельных элементов: х(3) = 3 Длину массива можно найти командой: length (x)
Переходим к двумерным массивам:
Задание в командной строке: x =
ans =
1 2 3 4
5 6 7 8
Задание отдельных элементов: х(2,3) = 7 Обращение к отдельной р-ой строке массива: у = Обращение к к-ому столбцу массива: у = Команда В=А(:,:) обращается ко всем элементам матрицы, т.е. создаёт копию матрицы А.
Также следует знать о стандартных матрицах:
- zeros(n,m) — матрица из нулей размера nxm
- ones(n,m) – матрица из единиц размера nxm
- rand(n,m) – матрица случайных чисел размера nxm
- eye(n,m) – матрица из единиц на главной диагонали размера nxm
11.1 Тригонометрические и гиперболические функции
Синусом комплексного переменного называется функция
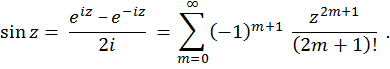
Косинус комплексного переменного есть функция
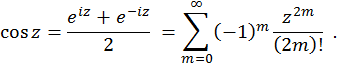
Гиперболический синус комплексного переменного определяется
так:
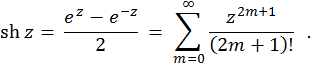
Гиперболический косинус комплексного переменного —
это функция
Отметим некоторые свойства вновь введеных функций.
A. Если x∈ ℝ , то cos x, sin x, ch x, sh x∈
ℝ .
Б. Имеет место следующая связь тригонометрических и
гиперболических функций:
cos iz=ch z; sin iz=ish z, ch
iz=cos z; sh iz=isin z.
В. Основные тригонометрическое и гиперболическое
тождества:
cos2z+sin2z=1;
ch2z-sh2z=1.
Доказательство основного гиперболического тождества.
![]()
Основное тригонометрическое тождество следует из оновного
гиперболического тождества при учете связи тригонометрических и гиперболических
функций (см. свойство Б)
Г Формулы сложения:
![]()
![]()
В частности,
![]()
![]()
Д. Для вычисления производных тригонометрических и
гиперболических функций следует применить теорему о почленном дифференцировании
степенного ряда. Получим:
(cos z)’=-sin z; (sin
z)’=cos z; (ch z)’=sh z; (sh z)’=ch z.
Е. Функции cos z, ch z четны, а функции
sin z, sh z нечетны.
Ж. (Периодичность) Функция ez периодична
с периодом 2π i. Функции cos z, sin z периодичны с периодом 2π , а функции ch
z, sh z периодичны с периодом 2πi. Более того,
![]()
Применяя формулы суммы, получаем
З. Разложения на действительную и мнимую части:
![]()
![]()
Если однозначная аналитическая функция f(z) отображает
биективно область D на область G, то D называется областью однолистности.
И. Область Dk={ x+iy | 2π k≤ y<2π (k+1)}
для любого целого k является областью однолистности функции ez,
которая отображает ее на область ℂ*
.
Доказательство. Из соотношения (5) следует инъективность
отображения exp:Dk→ ℂ
. Пусть w — любое ненулевое комплексное число. Тогда, решая уравнения ex=|w|
и
eiy =w/|w| с действительными переменными x и y (y выбираем из
полуинтеравала [2πk, 2π (k+1))), получим z=x+iy∈Dk
такое, что exp z=w. Сюръективность доказана.
Следствием предыдущего свойства является
К. Область значений. Область значений функций cos z,
sin z, ch z, sh z есть все поле комплексных чисел.
Л. Нули Решением уравнения sin z=0 является
множество {πk | k∈ ℤ } . Нули функции cos z — множество
{ π /2+πk | k∈
ℤ } . Нулями функции sh
z является множество { πki | k∈
ℤ} , а нули функции ch
z — множество { π/2i+πki | k∈
ℤ } .
Доказательство. Имеет место соотношения sin z=0 тогда и
только тогда, когда eiz -e-iz =0 Это равносильно соотношению
e2iz =0, что дает 2iz=2πik. Окончательно, z=2πk (k∈ ℤ ). Аналогично доказываются утверждения для
остальных функций.□
Функция tg z=sin z /cos z называется тангенсом, а функция
th z= sh
z/ ch z называется гиперболическим тангенсом. Производные тангенсов
вычисляются c использованием известного правила «производная
отношения»:
(tg z)’=1/cos2z , (th z)’= 1/ch2z .
Область допустимых значений тангенса tg z есть многосвязная
область ℂ \{π /2+πk | k∈
ℤ }
Тригонометрический калькулятор онлайн — примеры
Как произвести онлайн расчет синусов и косинусов, тангенсов
Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами. 1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан
1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.
Для включения того или иного режима измерения нажмите нужную кнопку:
где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.
В качестве самого простого примера найдем синус 90 градусов. Нажмите:
90
Ответ: единица
Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:
60
Решение: 0,5
Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.
Для их ввода необходимо переключить интерфейс, нажав , появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.
Преобразование с кнопкой Dms и Deg на калькуляторе
позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. производит обратный перевод – в формат «градусы; минуты; секунды».
Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:
35,140453 35,23459166666666666666
Переведем в прежний формат: 35,23459166666666666666 35,140453
Десятичный логарифм онлайн
Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:
1
Получается 0 в итоге. Для подсчета lg100 нажмем так:
100
Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.
Так же вычисляется натуральный логарифм, но кнопкой .
Как пользоваться памятью на калькуляторе
Существующие кнопки памяти: M+, M-, MR, MS, MC.
Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.
MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.
Пример. Внесем сто сорок пять в память программы:
145
После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:
На экране отобразится снова 145.
Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем , либо для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой получится 230, а во втором, после нажатия и получится 60.
Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.
Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!
Библиотека math
Библиотека является стандартной в Python и содержит много полезных математических функций и констант. Официальная документация Python выделяет следующие виды функций этого модуля:
Функции теории чисел и функции представления. Рассмотрим некоторые из них:
— возвращает количество сочетаний из элементов по элементам без повторений и без учёта порядка. Определим, сколькими способами можно выбрать 3 объекта из множества в 12 объектов (порядок не важен):
— возвращает факториал целого неотрицательного числа :
— возвращает наибольший общий делитель (НОД) для чисел-аргументов. Возможность определения НОДа для более чем двух чисел появилась в Python версии 3.9:
— возвращает наименьшее общее кратное (НОК) для чисел-аргументов. Функция появилась в Python версии 3.9:
— возвращает количество размещений из элементов по элементам без повторений и с учётом порядка. Если значение аргумента не задано, то возвращается количество перестановок множества из элементов:
— возвращает произведение элементов итерируемого объекта . Если пустой, то возвращается значение именованного аргумента :
Степенные и логарифмические функции. Некоторые из функций:
— возвращает значение экспоненциальной функции ex:
— возвращает значение логарифма от по основанию . Если значение аргумента не задано, то вычисляется натуральный логарифм. Вычисление производится по формуле :
— возвращает значение в степени . В отличие от операции , происходит преобразование обоих аргументов в вещественные числа:
Тригонометрические функции. Доступны функции синус (), косинус (), тангенс (), арксинус (), арккосинус (), арктангенс ()
Обратите внимание: угол задаётся и возвращается в радианах. Имеются особенные функции:
— возвращает Евклидово расстояние между точками и , заданными как итерируемые объекты одной длины:
— возвращает длину многомерного вектора с координатами, заданными в позиционных аргументах , и началом в центре системы координат
Для двумерной системы координат функция возвращает длину гипотенузы прямоугольного треугольника по теореме Пифагора:
Функции преобразования угла. Доступны функции:
math.degrees(x) — преобразует угол из радианов в градусы:
math.radians(x) — преобразует угол из градусов в радианы.
Гиперболические функции. Доступны функции , , , , , .
Специальные функции. Среди специальных функций интерес представляет Гамма-функция. Она описывает гладкую непрерывную функцию f(x) = (x — 1)!, график которой проходит через точки, соответствующие значениям функции факториала для целых чисел. Другими словами, гамма-функция интерполирует значения факториала для вещественных чисел:
В библиотеке можно воспользоваться значениями числа пи () и экспоненты ().
Символьные операции линейной алгебры
Линейная алгебра — главная особенность системы MATLAB. Но реализована она численными методами. В этом разделе описаны функции линейной алгебры, обеспечивающие символьные преобразования и вычисления векторов и матриц, существенно расширяющие типовые средства линейной алгебры системы MATLAB.
Для создания диагональных матриц и извлечения из них диагональных элементов служит функция diag(V,K): если V — вектор с N компонентами, то формируется квадратная матрица с размером N+ABS(K), в которой на K‑ой диагонали размещен вектор V. При K = 0 вектор V располагается на главной диагонали, при K > 0 на K‑ой диагонали сверху, а при K < 0 — снизу относительно главной диагонали. Помимо заданных, остальные элементы матриц — нули. Применение этой функции вполне очевидно, как и функции triu для формирования верхней треугольной матрицы и tril — для формирования нижней треугольной матрицы.
Для обращения (инвертирования) матрицы в символьном виде используется функция inv:
>> inv() ans = [ d/(a*d-b*c), -b/(a*d-b*c)] [ -c/(a*d-b*c), a/(a*d-b*c)]
Функция det(X) вычисляет детерминант квадратной матрицы в символьном виде.
Для вычисления ранга квадратной матрицы используется функция rank:
>> rank() ans = 2
Для приведения матрицы к верхней треугольной форме используется функция rref. Функция = rref(A,tol) осуществляет приведение матрицы к треугольной форме, используя метод исключения Гаусса с частичным выбором ведущего элемента для заданного значения порога допустимости tol.
Функция Z = null(A) возвращает матрицу Z, столбцы которой являются базисом нуль-пространства целочисленной матрицы A. Число столбцов матрицы Z задает размер нуль-пространства. При этом A*Z = 0, а если матрица A имеет полный ранг, то матрица Z будет пустой.
Функция colspace(A) возвращает матрицу, столбцы которой являются образующими базиса пространства. Ранг целочисленной матрицы A равен size(B,2). Для вычисления собственных значений и собственных векторов матриц используется функция eig, имеющая ряд форм записи:
LAMBDA=eig(A) — формирует символьный вектор LAMBDA собственных значений квадратной матрицы A.
=eig(A) — возвращает матрицу V, столбцы которой являются векторами собственных значений матрицы A, и диагональную матрицу D собственных значений. Если размеры V и A одинаковы, то A имеет полную систему независимых собственных векторов. При этом A*V = V*D.
=eig(A) — дополнительно к сказанному возвращает вектор индексов P, длина которого равна числу линейно независимых векторов. При этом A*V= V*D(P,P).
LAMBDA=eig(VPA(A)) и = eig(VPA(A)) — возвращают численные значения собственных векторов и собственных значений в формате арифметики с произвольной точностью. Если матрица A не имеет полной системы собственных векторов, то столбцы матрицы V будут линейно зависимыми.
Для символьного вычисления матричных функций и операций линейной алгебры служит пакет расширения MuPad linalg:: (рис. 5). С его имени начинаются имена функций этого пакета. На рис. 5 показаны некоторые операции линейной алгебры и окно с разделом справки по операции транспонирования матриц.
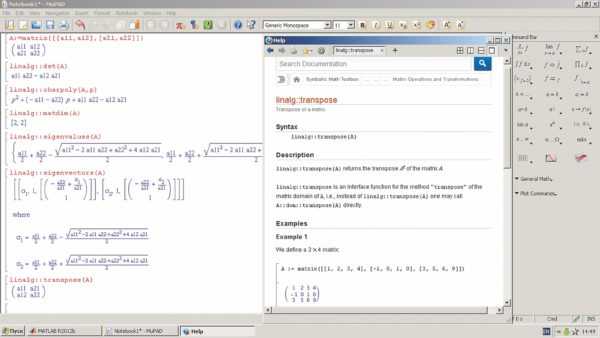
Рис. 5. Вычисление некоторых матричных функций в ноутбуке MuPad
О богатстве операций линейной алгебры свидетельствует ноутбук системы MuPad (рис. 6). В правой части его окна открыты списки основных математических операций General Math и основных групп операций линейной алгебры.
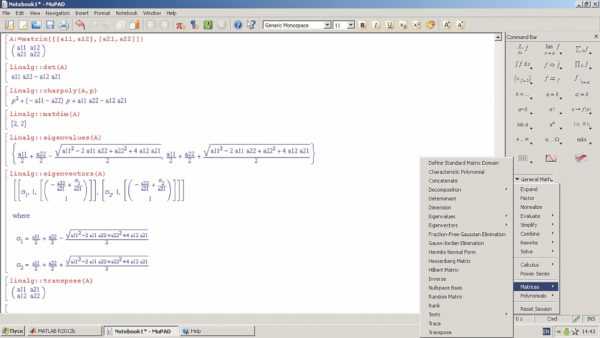
Рис. 6. Окно ноутбука MuPad: списки основных математических операций General Math и основных групп операций линейной алгебры
2.3. Основные матричные операции
При использовании матричных
операций следует помнить, что для
сложения или вычитания матрицы должны
быть одного размера, а при перемножении
число столбцов первой матрицы обязано
равняться числу строк второй матрицы.
Сложение и вычитание матриц, так же как
чисел и векторов, осуществляется при
помощи знаков плюс и минус
а
умножение — знаком звездочка *.
Введем матрицу размером 3×2
Умножение
матрицы на число тоже осуществляется
при помощи звездочки, причем умножать на
число можно как справа, так и слева.
Возведение квадратной матрицы в целую
степень производится с использованием
оператора ^
Проверьте
полученный результат, умножив матрицу Р
саму на себя.
Свойства[]
Связь с тригонометрическими функциями
Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.
shx=−isin(ix),chx=cos(ix),thx=−itg(ix){\displaystyle \mathop {\mathrm {sh} } \,x=-i\sin(ix),\quad \mathop {\mathrm {ch} } \,x=\cos(ix),\quad \mathop {\mathrm {th} } \,x=-i\mathop {\mathrm {tg} } \,(ix)}.
Важные тождества
- shx+chx=ex{\displaystyle \mathop {\mathrm {sh} } \,x+\mathop {\mathrm {ch} } \,x=e^{x}}
- ch2x−sh2x=1{\displaystyle \mathop {\mathrm {ch} } ^{2}x-\mathop {\mathrm {sh} } ^{2}x=1}
-
Чётность:
- sh(−x)=−shx{\displaystyle \mathop {\mathrm {sh} } (-x)=-\mathop {\mathrm {sh} } \,x}
- ch(−x)=chx{\displaystyle \mathop {\mathrm {ch} } (-x)=\mathop {\mathrm {ch} } \,x}
- th(−x)=−thx{\displaystyle \mathop {\mathrm {th} } (-x)=-\mathop {\mathrm {th} } \,x}
- Формулы сложения:
- sh(x+y)=shxchy+shychx{\displaystyle \mathop {\mathrm {sh} } (x+y)=\mathop {\mathrm {sh} } \,x\,\mathop {\mathrm {ch} } \,y+\mathop {\mathrm {sh} } \,y\,\mathop {\mathrm {ch} } \,x}
- ch(x+y)=chxchy+shyshx{\displaystyle \mathop {\mathrm {ch} } (x+y)=\mathop {\mathrm {ch} } \,x\,\mathop {\mathrm {ch} } \,y+\mathop {\mathrm {sh} } \,y\,\mathop {\mathrm {sh} } \,x}
- Формулы двойного угла:
- sh2x=2chxshx=2thx1−th2x{\displaystyle \mathop {\mathrm {sh} } \,2x=2\mathop {\mathrm {ch} } \,x\,\mathop {\mathrm {sh} } \,x={\frac {2\mathop {\mathrm {th} } \,x}{1-\mathop {\mathrm {th} } ^{2}x}}}
- ch2x=ch2x+sh2x=1+th2x1−th2x{\displaystyle \mathop {\mathrm {ch} } \,2x=\mathop {\mathrm {ch} } ^{2}x+\mathop {\mathrm {sh} } ^{2}x={\frac {1+\mathop {\mathrm {th} } ^{2}x}{1-\mathop {\mathrm {th} } ^{2}x}}}
- th2x=2thx1+th2x{\displaystyle \mathop {\mathrm {th} } \,2x={\frac {2\mathop {\mathrm {th} } \,x}{1+\mathop {\mathrm {th} } ^{2}x}}}
- Производные:
- (shx)′=chx{\displaystyle (\mathop {\mathrm {sh} } \,x)^{\prime }=\mathop {\mathrm {ch} } \,x}
- (chx)′=shx{\displaystyle (\mathop {\mathrm {ch} } \,x)^{\prime }=\mathop {\mathrm {sh} } \,x}
- (thx)′=1ch2x{\displaystyle (\mathop {\mathrm {th} } \,x)^{\prime }={\frac {1}{\mathop {\mathrm {ch} } ^{2}x}}}
- shx=∫xchtdt{\displaystyle \mathop {\mathrm {sh} } \,x=\int _{0}^{x}\mathop {\mathrm {ch} } tdt}
- chx=1+∫xshtdt{\displaystyle \mathop {\mathrm {ch} } \,x=1+\int _{0}^{x}\mathop {\mathrm {sh} } tdt}
- thx=∫xdtch2t{\displaystyle \mathop {\mathrm {th} } \,x=\int _{0}^{x}{\frac {dt}{\mathop {\mathrm {ch} } ^{2}t}}}
- Интегралы:
- ∫shxdx=chx+C{\displaystyle \int \mathop {\mathrm {sh} } \,x\,dx=\mathop {\mathrm {ch} } \,x+C}
- ∫chxdx=shx+C{\displaystyle \int \mathop {\mathrm {ch} } \,x\,dx=\mathop {\mathrm {sh} } \,x+C}
- ∫thxdx=lnchx+C{\displaystyle \int \mathop {\mathrm {th} } \,x\,dx=\ln \mathop {\mathrm {ch} } \,x+C}
- ∫1ch2xdx=thx+C{\displaystyle \int {\frac {1}{\mathop {\mathrm {ch} } ^{2}x}}\,dx=\mathop {\mathrm {th} } \,x+C}
- ∫1sh2xdx=−cthx+C{\displaystyle \int {\frac {1}{\mathop {\mathrm {sh} } ^{2}x}}\,dx=-\mathop {\mathrm {cth} } \,x+C}
Разложение в степенные ряды
- shx=x+x33!+x55!+x77!+…=∑n=∞x2n+1(2n+1)!{\displaystyle \mathop {\mathrm {sh} } \,x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\ldots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}
- chx=1+x22!+x44!+x66!+…=∑n=∞x2n(2n)!{\displaystyle \mathop {\mathrm {ch} } \,x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\ldots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}}
- thx=x−x33+2×515−17×7315+…=∑n=1∞(−1)n−122n(22n−1)Bnx2n−1(2n)!,|x|<π2{\displaystyle \mathop {\mathrm {th} } \,x=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\ldots =\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{n}x^{2n-1}}{(2n)!}},\quad |x|<{\frac {\pi }{2}}}
- cthx=1x+x3−x345+2×5945+…=1x+∑n=1∞(−1)n−122nBnx2n−1(2n)!,<|x|<π{\displaystyle \mathop {\mathrm {cth} } \,x={\frac {1}{x}}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\ldots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}B_{n}x^{2n-1}}{(2n)!}},\quad 0<|x|<\pi } (Ряд Лорана)
Здесь Bn{\displaystyle B_{n}} — числа Бернулли.
Аналитические свойства
Гиперболический синус и гиперболический косинус аналитичны во всей комплексной плоскости, за исключением существенно особой точки на бесконечности. Гиперболический тангенс аналитичен везде, кроме полюсов в точках z=iπ(n+12){\displaystyle z=i\pi (n+1/2)}, где n{\displaystyle n} — целое. Вычеты во всех этих полюсах равны единице. Гиперболический котангенс аналитичен везде, кроме точек z=iπn{\displaystyle z=i\pi n}, вычеты его в этих полюсах также равны единице.
MATLAB как язык программирования
М-файл
А еще MATLAB – это язык программирования, используемый непосредственно при работе с программой. Не будем вдаваться в подробности, скажем только, что программы, написанные на языке MATLAB, бывают двух видов: функции и скрипты.
MATLAB — серьезное средство для серьезных ребят
Основной рабочий файл программы – М-файл. Это бесконечный текстовый файл, и именно в нем происходит непосредственно программирование вычислений. Кстати, пусть Вас не пугает это слово – для того, чтобы работать в MATLAB, вовсе не нужно быть профессиональным программистом.
М-файлы делятся на
- М-сценарии. М-сценарий – самый простой тип M-файла, у которого отсутствуют входные и выходные аргументы. Данный файл используется для автоматизации многократно повторяемых вычислений.
- M-функции. М-функции – это М-файлы, допускающие наличие входных и выходных аргументов.
Для того чтобы наглядно показать, как происходит работа в MATLAB, приведем ниже пример создания функции в матлабе. Данная функция будет вычислять среднее значение вектора.function y = average (x)% AVERAGE Среднее значение элементов вектора.% AVERAGE(X), где X — вектор. Вычисляет среднее значение элементов вектора.% Если входной аргумент не является вектором, генерируется ошибка. = size(x); if (~((m == 1) | (n == 1)) | (m == 1 & n == 1)) error(‘Входной массив должен быть вектором’) end y =sum(x)/length(x); % Собственно вычисление
Строка определения функции сообщает системе MATLAB, что файл является М-функцией, а также определяет список входных аргументов. Так, строка определения функции average имеет вид: function y = average(x)
Где:
- function — ключевое слово, определяющее М-функцию;
- y — выходной аргумент;
- average — имя функции;
- x — входной аргумент.
Итак, чтобы написать функцию в матлабе, необходимо помнить, что каждая функция в системе MATLAB содержит строку определения функции, подобную приведенной.
Безусловно, такой мощный пакет нужен не только для того, чтобы облегчить жизнь студентам. В настоящее время MATLAB, с одной стороны, очень популярен среди специалистов многих научных и инженерных отраслей. С другой стороны, возможность работы с большими матрицами делает MATLAB незаменимым инструментом финансовых аналитиков, позволяющим решить намного больше задач, чем, к примеру, известный всем Excel. Подробнее о том, как сделать презентацию на компьютере вы можете прочитать в обзорной статье.
Применение[]
Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций.
Аналогично тому, как матрицы вида (cosxsinx−sinxcosx){\displaystyle {\begin{pmatrix}\cos x&\sin x\\-\sin x&\cos x\end{pmatrix}}} описывают повороты двумерного евклидова пространства, матрицы (chxshxshxchx){\displaystyle {\begin{pmatrix}\mathop {\mathrm {ch} } \,x&\mathop {\mathrm {sh} } \,x\\\mathop {\mathrm {sh} } \,x&\mathop {\mathrm {ch} } \,x\end{pmatrix}}} описывают повороты в простейшем двумерном пространстве Минковского. В связи с этим гиперболические функции часто встречаются в теории относительности.
Однородная веревка или цепочка, свободно подвешенная за свои концы, приобретает форму графика функции y=chx{\displaystyle y=\mathop {\mathrm {ch} } \,x} (в связи с чем график гиперболического косинуса иногда называют цепной линией). Это обстоятельство используется при проектировании арок, поскольку форма арки в виде перевёрнутой цепной линии наиболее удачно распределяет нагрузку.
4.5 Печать графиков
Пункт Print в меню
File и команда print
печатают графику MatLab. Меню Print
вызывает диалоговое окно, которое
позволяет выбирать общие стандартные
варианты печати. Команда print
обеспечивает большую гибкость при
выводе выходных данных и позволяет
контролировать печать из М-файлов.
Результат может быть послан прямо на
принтер, выбранный по умолчанию, или
сохранен в заданном файле.
5. Примеры программ
В этом разделе приведены
наиболее употребительные алгоритмы,
используемые при анализе многомерных
данных. Рассмотрены как простейшие
методы преобразования данных так и
алгоритмы для анализа данных — PCA, PLS.
Степень и логарифмические функции
Вероятнее всего, вы чаще всего сталкиваетесь со степенями и логарифмами, чем с гиперболическими или тригонометрическими функциями. К счастью, модуль math предоставляет множество функций, которые помогут нам вычислить логарифмы.
Вы можете использовать для вычисления log заданного числа x для данной базы. Если вы оставите необязательный аргумент базы, log x будет вычисляться до базы e. Здесь e — математическая константа, значение которой равно 2.71828182 …. и к ней можно получить доступ с использованием . Кстати, Python также позволяет вам получить доступ к другой константе π, используя .
Если вы хотите рассчитать значения логарифма base-2 или base-10, использование и вернет более точные результаты, чем и . Имейте в виду, что функция отсутствует, поэтому вам нужно будет использовать для вычисления значений логарифма базы-3. То же самое касается всех других баз.
Если значение, логарифм которого вы вычисляете, очень близко к 1, вы можете использовать . в означает 1 плюс. Поэтому вычисляет, где x близок к нулю. Однако результаты более точны с .
Вы также можете рассчитать значение числа x, возведённого в степень y, используя . Перед вычислением степени эта функция преобразует оба аргумента в тип float. Если вы хотите, чтобы конечный результат был вычислен в точных целых степенях, вы должны использовать встроенную функцию или оператор .
Вы также можете вычислить квадратный корень любого заданного числа x, используя , но то же самое можно также сделать, используя .
1 |
import math |
2 |
|
3 |
math.exp(5) # returns 148.4131591025766 |
4 |
math.e**5 # returns 148.4131591025765 |
5 |
|
6 |
math.log(148.41315910257657) # returns 5.0 |
7 |
math.log(148.41315910257657, 2) # returns 7.213475204444817 |
8 |
math.log(148.41315910257657, 10) # returns 2.171472409516258 |
9 |
|
10 |
math.log(1.0000025) # returns 2.4999968749105643e-06 |
11 |
math.log1p(0.0000025) # returns 2.4999968750052084e-06 |
12 |
|
13 |
math.pow(12.5, 2.8) # returns 1178.5500657314767 |
14 |
math.pow(144, 0.5) # returns 12.0 |
15 |
math.sqrt(144) # returns 12.0 |
Math — математические функции в Python
Эта статья посвящена математическим функциям в Python. Для выполнения математических операций необходим модуль math .
Что такое модуль?
В C и C++ есть заголовочные файлы, в которых хранятся функции, переменные классов и так далее. При включении заголовочных файлов в код появляется возможность не писать лишние строки и не использовать одинаковые функции по несколько раз. Аналогично в Python для этого есть модули, которые включают функции, классы, переменные и скомпилированный код. Модуль содержит группу связанных функций, классов и переменных.
- Модули, написанные на Python ( .py ).
- Модули, написанные на C и загружаемые динамически ( .dll , .pyd , .so , .sl и так далее).
- Модули, написанные на C , но связанные с интерпретатором.
Для получения списка модулей, написанных на C , но связанных с Python, можно использовать следующий код.
Как видно из списка выше, модуль math написан на C , но связан с интерпретатором. Он содержит математические функции и переменные, о которых дальше и пойдет речь.
Функции представления чисел
ceil() и floor() — целая часть числа
Сeil() и floor() — функции общего назначения. Функция ceil округляет число до ближайшего целого в большую сторону. Функция floor убирает цифры десятичных знаков. Обе принимают десятичное число в качестве аргумента и возвращают целое число.
Пример:
Функция fabs() — абсолютное значение
Функция fabs используется для вычисления абсолютного значения числа. Если число содержит любой отрицательный знак ( — ), то функция убирает его и возвращает положительное дробное число.
Пример:
factorial() — функция факториала
Эта функция принимает положительное целое число и выводит его факториал.
Пример:
Примечание: при попытке использовать отрицательное число, возвращается ошибка значения ( Value Error ).
Пример:
Функция fmod() — остаток от деления
Функция fmod(x,y) возвращает x % y . Разница в том, что выражение x % y работает только с целыми числами, а эту функцию можно использовать и для чисел с плавающей точкой.
Пример:
Функция frexp()
Эта функция возвращает мантиссу и показатель степени в виде пары ( m,n ) любого числа x , решая следующее уравнение.
Пример:
Функция fsum() — точная сумма float
Вычисляет точную сумму значений с плавающей точкой в итерируемом объекте и сумму списка или диапазона данных.
Пример:
Функции возведения в степень и логарифма
Эта функция принимает один параметр в виде дробного числа и возвращает e^x .
Пример:
Функция expm1()
Эта функция работает так же, как и exp , но возвращает exp(x)-1 . Здесь, expm1 значит exm-m-1 , то есть, exp-minus-1 .
Пример:
Функция log() — логарифм числа
Функция log(x) находит логарифм числа x по основанию e (по умолчанию). base — параметр опциональный. Если нужно вычислить логарифм с определенным основанием, его нужно указать.
Пример:
Эта функция похожа на функцию логарифма, но добавляет 1 к x . log1p значит log-1-p , то есть, log-1-plus .
Пример:
Вычисляет логарифм по основанию 10.
Пример:
Функция pow() — степень числа
Используется для нахождение степени числа. Синтаксис функции pow(Base, Power) . Она принимает два аргумента: основание и степень.
Пример:
Функция sqrt() — квадратный корень числа
Эта функция используется для нахождения квадратного корня числа. Она принимает число в качестве аргумента и находит его квадратный корень.
Пример:
Тригонометрические функции
В Python есть следующие тригонометрические функции.
| Функция | Значение |
|---|---|
| sin | принимает радиан и возвращает его синус |
| cos | принимает радиан и возвращает его косинус |
| tan | принимает радиан и возвращает его тангенс |
| asin | принимает один параметр и возвращает арксинус (обратный синус) |
| acos | принимает один параметр и возвращает арккосинус (обратный косинус) |
| atan | принимает один параметр и возвращает арктангенс (обратный тангенс) |
| sinh | принимает один параметр и возвращает гиперболический синус |
| cosh | принимает один параметр и возвращает гиперболический косинус |
| tanh | принимает один параметр и возвращает гиперболический тангенс |
| asinh | принимает один параметр и возвращает обратный гиперболический синус |
| acosh | принимает один параметр и возвращает обратный гиперболический косинус |
| atanh | принимает один параметр и возвращает обратный гиперболический тангенс |
Пример:
Эти функции преобразуют угол. В математике углы можно записывать двумя способами: угол и радиан. Есть две функции в Python, которые конвертируют градусы в радиан и обратно.








![Тригонометрические выражения и тригонометрические формулы [wiki.eduvdom.com]](http://site-edu.ru/wp-content/uploads/a/6/6/a6665d82afd91afb9e55932b4d16d99b.png)





















