Точки лагранжа

Смотреть похожие работы

Проект «Разрушительное действие радиации на живой организм»

Доступна к просмотру полнотекстовая версия работы

Актуальность. Окружающий нас мир радиоактивен. «Большой взрыв», с которого, как сейчас полагают ученые, началось существование нашей Вселенной, сопровождался образованием радиоактивных элементов и радиоактивным изучением. С тех пор радиация постоянно…

Проектная работа «Парадокс Фергюсона. Планетарные механизмы»

«Я знаю, что ничего не знаю», — однажды сказал древнегреческий философ Сократ и был прав. Даже в таких точных науках, как математика, физика или логика, есть задачи, решить которые не под силу лучшим умам человечества. По сути, механизм Фергюсона одн…

Проект «Природа родного края на координатной плоскости»

Материал по теме «Координатная плоскость» изучается в курсе математики 6 класса. На изучение темы отводится 4 часа. Эта тема по времени приходится на конец апреля – начало мая, когда учитель и дети загружены работой по завершению учебного года. Умени…

Проектная работа «Звездные компасы»

В современном мире человек все больше полагается на помощь «умных технологий». Зачем уметь ориентироваться на местности, если есть навигатор, способный проложить любой маршрут? Зачем уметь различать созвездия, если для этого созданы специальные прило…

Исследовательский проект «Вклад математики в изучении космоса»

Доступна к просмотру полнотекстовая версия работы

Начиная с ХХ века происходит активное физическое освоение космического пространства. Человек всегда стремился раздвинуть рамки известного ему мира, и каждый успех в этом направлении неизменно стимулировал развитие человеческого общества, его культуры…

Приложения для космических полетов

Солнце – Земля

ACE

Солнце – Земля L 1 подходит для наблюдений за системой Солнце – Земля. Объекты здесь никогда не затеняются Землей или Луной, и, наблюдая за Землей, всегда видно освещенное солнцем полушарие. Первой миссией этого типа была миссия 1978 года International Sun Earth Explorer 3 (ISEE-3), использовавшаяся в качестве межпланетного монитора раннего предупреждения о штормах для солнечных возмущений. С июня 2015 года DSCOVR вращается вокруг точки L 1. И наоборот, он также полезен для космических солнечных телескопов, поскольку он обеспечивает непрерывный обзор Солнца и любой космической погоды (включая солнечный ветер и корональные выбросы массы ) достигают L 1 за час до Земли. Солнечные и гелиосферные миссии, в настоящее время расположенные вокруг L 1, включают Солнечную и гелиосферную обсерваторию, Wind и Advanced Composition Explorer. Запланированные миссии включают межзвездное картографирование и зонд ускорения (IMAP).

Солнце – Земля L 2 — хорошее место для космических обсерваторий. Поскольку объект вокруг L 2 будет сохранять одинаковое относительное положение относительно Солнца и Земли, экранирование и калибровка намного проще. Однако он находится немного за пределами досягаемости тени Земли, поэтому солнечное излучение не полностью блокируется на L 2. Космические аппараты обычно вращаются вокруг L 2, избегая частичных солнечных затмений для поддержания постоянной температуры. Из местоположений около L 2 Солнце, Земля и Луна находятся на небе относительно близко друг к другу; это означает, что большой солнцезащитный козырек с телескопом на темной стороне может позволить телескопу пассивно охлаждаться примерно до 50 К — это особенно полезно для инфракрасной астрономии и наблюдений космического микроволнового фона. Космический телескоп Джеймса Уэбба должен быть расположен на L 2.

Солнце – Земля L 3 было популярным местом для размещения «Противоземли » в pulp научной фантастике и комиксах. Когда стало возможным наблюдение из космоса с помощью спутников и зондов, оказалось, что такого объекта нет. Солнце – Земля L 3 нестабильно и очень долго не может содержать естественный объект, большой или маленький. Это потому, что гравитационные силы других планет сильнее, чем у Земли (Венера, например, находится в пределах 0,3 а.е. от этого L 3 каждые 20 месяцы).

Космический корабль, движущийся по орбите вокруг Солнца и Земли L 3, сможет внимательно следить за эволюцией активных областей солнечных пятен до того, как они повернутся в геоэффективное положение, чтобы можно было получить раннее предупреждение за 7 дней. выпускаться NOAA Центром прогнозирования космической погоды. Более того, спутник около Солнца – Земля L 3 обеспечит очень важные наблюдения не только для прогнозов Земли, но и для поддержки дальнего космоса (прогнозы Марса и пилотируемый полет к ). В 2010 году были изучены траектории перехода космических аппаратов к Солнцу – Земле L 3 и рассмотрено несколько проектов.

Миссии к лагранжевым точкам обычно вращаются вокруг точек, а не занимают их напрямую.

Еще одно интересное и полезное свойство коллинеарных лагранжевых точек и связанных с ними орбит Лиссажу состоит в том, что они служат «шлюзами» для управления хаотическими траекториями межпланетной транспортной сети.

Земля – Луна

Земля – Луна L 1 обеспечивает сравнительно легкий доступ к лунной и земной орбитам с минимальным изменением скорости, и это дает преимущество для размещения пилотируемой космической станции на полпути предназначен для перевозки грузов и персонала на Луну и обратно.

Земля – Луна L 2 использовался для спутника связи, покрывающего обратную сторону Луны, например, , запущенный в 2018 г., и было бы «идеальным местом» для склада топлива как части предлагаемой архитектуры космического транспорта на базе депо.

Солнце – Венера

Ученые из Фонд B612 планировал использовать точку L 3 Венеры для размещения запланированного телескопа Sentinel, который был направлен на орбиту Земли. и составить каталог околоземных астероидов.

Солнце-Марс

В 2017 году идея размещения магнитного дипольного щита на Солнце-Марс L 1 точка для использования в качестве искусственной магнитосферы Марса обсуждалась на конференции NASA. Идея состоит в том, что это защитит атмосферу планеты от солнечного излучения и солнечных ветров.

Нынешние способы космических полётов

Сегодня перемещение между объектами Солнечной системы, например, путешествие с Земли на Марс, обычно требует так называемого перелёта по эллипсу Гомана. Носитель запускается, а затем ускоряется до тех пор, пока не оказывается дальше орбиты Марса. Около красной планеты ракета притормаживает и начинает вращаться вокруг цели своего назначения. И для ускорения, и для торможения она сжигает много топлива, но при этом эллипс Гомана остаётся одним из самых эффективных способов перемещения между двумя объектами в космосе.

Эллипс Гомана- Дуга I — перелет с Земли на Венеру. Дуга II-перелет с Венеры на Марс Дуга III- возвращение с Марса на Землю.

Используются также и гравитационные маневры, которые могут быть ещё более эффективными. Совершая их, космический корабль ускоряется, используя силу притяжения крупного небесного тела. Прибавка в скорости получается очень значительной почти без использования горючего. Мы применяем эти маневры всякий раз, когда отправляем свои станции в далёкий путь от Земли. Однако если кораблю после гравитационного маневра нужно выйти на орбиту какой-то планеты, ему всё равно приходится замедляться. Вы, конечно, помните, что это требует топлива.

Значения Солнечной системы

В этой таблице перечислены примерные значения L 1, L 2 и L 3 в Солнечной системе. В расчетах предполагается, что два тела вращаются по идеальному кругу с разделением, равным большой полуоси, и никаких других тел поблизости нет. Расстояния измеряются от центра масс большего тела, где L 3 указывает отрицательное положение. Столбцы с процентным соотношением показывают, как расстояния сравниваются с большой полуосью. Например. для Луны L 1 находится на расстоянии 326400 км от центра Земли, что составляет 84,9% расстояния Земля – Луна или 15,1% перед Луной; L 2 находится в 448900 км от центра Земли, что составляет 116,8% расстояния Земля – Луна или 16,8% за пределами Луны; а L 3 находится на -381700 км от центра Земли, что составляет 99,3% расстояния Земля-Луна или 0,7084% перед «отрицательным» положением Луны.

Лагранжевые точки в Солнечной системе
Пара тел	Большая полуось (SMA)	L1	1 — L 1 / SMA (%)	L2	L2/ SMA — 1 ( %)	L3	1 + L 3 / SMA (%)
Земля – Луна	3,844 × 10 м	3,2639 × 10 м	15,09	4,489 × 10 м	16,78	−3,8168 × 10 м	0,7084
Солнце – Меркурий	5,7909 × 10 м	5,7689 × 10 м	0,3806	5,813 × 10 м	0,3815	-5,7909 × 10 м	0,000009683
Солнце – Венера	1,0821 × 10 м	1,072 × 10 м	0,9315	1,0922 × 10 м	0,9373	−1,0821 × 10 м	0,0001428
Солнце – Земля	1,496 × 10 м	1,4811 × 10 м	0,997	1,511 × 10 м	1,004	-1,496 × 10 м	0,0001752
Солнце – Марс	2,2794 × 10 м	2,2686 × 10 м	0,4748	2,2903 × 10 м	0,4763	−2,2794 × 10 м	0,00001882
Солнце – Юпитер	7,7834 × 10 м	7,2645 × 10 м	6,667	8,3265 × 10 м	6,978	−7,7791 × 10 м	0,05563
Солнце – Сатурн	1,4267 × 10 м	1,3625 × 10 м	4,496	1,4928 × 10 м	4,635	−1,4264 × 10 м	0,01667
Солнце – Уран	2,8707 × 10 м	2,8011 × 10 м	2,421	2,9413 × 10 м	2,461	−2,8706 × 10 м	0,002546
Солнце – Нептун	4,4984 × 10 м	4,3834 × 10 м	2,557	4,6154 × 10 м	2,602	-4,4983 × 10 м	0,003004

точками Лагранжа

Пять точек Лагранжа помечены и определены следующим образом:

L1точка

Точка L 1 лежит на линии, определяемой двумя большими массами M 1 и M 2, и между ними. Это точка, в которой гравитационное притяжение M 2 частично компенсирует притяжение M 1. Объект, который вращается вокруг Солнца ближе, чем Земля, обычно имеет более короткий орбитальный период, чем Земля, но это игнорирует влияние собственного гравитационного притяжения Земли. Если объект находится непосредственно между Землей и Солнцем, то гравитация Земли противодействует некоторому притяжению Солнца к объекту и, следовательно, увеличивает период обращения объекта. Чем ближе к Земле объект, тем сильнее этот эффект. В точке L 1 период обращения объекта становится точно равным периоду обращения Земли. L 1 находится примерно в 1,5 миллиона километров от Земли, или 0,01 а.е., 1/100 расстояния до Солнца.

L2точка

L Точка 2 лежит на линии, проходящей через две большие массы, за меньшей из двух. Здесь гравитационные силы двух больших масс уравновешивают центробежное воздействие на тело при L 2. На противоположной стороне Земли от Солнца орбитальный период объекта обычно больше, чем у Земли. Дополнительное притяжение земной силы тяжести уменьшает орбитальный период объекта, и в точке L 2 этот период обращения становится равным земному. Подобно L 1, L 2 находится примерно в 1,5 миллиона километров или 0,01 а.е. от Земли.

L3точка

Точка L 3 лежит на линии, определяемой двумя большими массами, за пределами большей из двух. В системе Солнце – Земля точка L 3 существует на противоположной стороне от Солнца, немного за пределами орбиты Земли и немного дальше от Солнца, чем Земля. Такое размещение происходит потому, что на Солнце также действует гравитация Земли, и поэтому он вращается вокруг барицентра двух тел, который находится внутри тела Солнца. Объект, находящийся на расстоянии Земли от Солнца, будет иметь период обращения одного года, если учитывать только гравитацию Солнца. Но объект на противоположной стороне Солнца от Земли и прямо на одной линии с обоими «ощущает» гравитацию Земли, немного добавляющую к солнечной, и поэтому должен вращаться немного дальше от Солнца, чтобы иметь такой же период в 1 год. Именно в точке L 3 комбинированное притяжение Земли и Солнца заставляет объект вращаться по орбите с тем же периодом, что и Земля, фактически вращаясь вокруг массы Земля + Солнце с барицентром Земля-Солнце в одном фокусе. своей орбиты.

L4и L 5 точки

Точки L 4 и L 5 лежат в третьих углах двух равносторонние треугольники в плоскости орбиты, общее основание которых является линией между центрами двух масс, так что точка находится позади (L 5) или впереди (L 4) меньшей массы по отношению к орбите вокруг большей массы.

Треугольные точки (L 4 и L 5) являются устойчивыми равновесиями при условии, что отношение M 1/M2больше 24,96. Это относится к системе Солнце – Земля, системе Солнце – Юпитер и, в меньшей степени, системе Земля – Луна. Когда тело в этих точках возмущается, оно удаляется от точки, но коэффициент, противоположный тому, который увеличивается или уменьшается из-за возмущения (скорость, вызванная гравитацией или угловым моментом), также будет увеличиваться или уменьшаться, искривляя траекторию объекта. в устойчивую фасоль -образную орбиту вокруг точки (как видно в вращающейся системе координат).

В отличие от L 4 и L 5, где существует устойчивое равновесие, точки L 1, L 2 и L 3 являются положениями неустойчивого равновесия. Любой объект, движущийся по орбите в L 1, L 2 или L 3, будет иметь тенденцию выпадать с орбиты; поэтому там редко можно встретить природные объекты, и космические корабли, населяющие эти районы, должны использовать стоянку для поддержания своего местоположения.

Точки Лагранжа в фантастике[править]

Чаще всего в фантастике встречаются точки L4 и L5. В них удобно размещать космические станции и другие объекты, которые не должны далеко удаляться от отведённого для них места. Впрочем, остальные точки тоже получают долю внимания.

Литератураправить

Жюль Верн, «Из пушки на Луну» — едва ли не первопример твёрдой научной фантастики, по нынешним временам, однако, не совсем точный: ядро с путешественниками должно преодолеть так называемую «нейтральную точку», чтобы дальше уже свободно падать на Луну. Для ньютоновской физики, понятия не имеющей о космических скоростях, это в порядке вещей. Кстати, пролетели мимо Луны.
Бен Бова, «Колония» — обитаемая станция в точке L4 системы Земля — Луна.
Гарри Гаррисон, «Возвращение к звёздам» — в точках L4 и L5 расположены колонии, состоящие из большого количества отдельных космических станций.
Артур Кларк, «Лунная пыль» — в точках Лагранжа L1 и L2 системы Земля — Луна расположены две обитаемые космические станции.
Ларри Нивен, «Дар с Земли» — космическая обсерватория в троянской точке системы Солнце — Нептун.
Артур Кларк, «2010: Одиссея Два» (2010: Odyssey Two) — в точке Лагранжа между Юпитером и Ио должен был занять позицию корабль «Дискавери», однако ввиду неустойчивости этой точки он начал смещаться к Ио.
Чарльз Шеффилд, «Единение разумов» — в точке L5 системы Солнце — Юпитер расположена космическая свалка. Собственно, она и так там расположена.
Орсон Скотт Кард, «Игра Эндера» — Боевая школа находится либо в L4 либо в L5. В спин-оффе «Дети флота», становится известно, что станцию проектировали ещё раньше, ведь точка — удобная. Потом её забрал себе Международный флот. После окончания Третьего вторжения, станцию переименовали в Школу флота, где готовят не будущих генералов, а будущих колонизаторов.
Михаил Пухов, «Путь к Земле»(«Кон-Тики») — во внутренней точке либрации системы Земля — Луна располагается автоматический танкер «Лагранж» (ага!), эдакая космическая бензоколонка.

Телесериалыправить

Вавилон 5 — космическая станция «Вавилон 5» расположена в точке L5 системы звезда Тигр (Эпсилон Эридана) — планета Евфрат.

Веб-комиксыправить

Внезапно в фэнтези «Перчинка и Морковка» («Pepper and Carrot») — попытка Перчинки утилизировать «неправильные» зелья с помощью Черной Дыры. Да, магия Хаоса магией Хаоса, но элементарной физики даже в фэнтези никто не отменял.

Аниме и мангаправить

Сериал Mobile Suit Gundam 00 — в точке L2 системы Земля — Луна располагается главная база Celestial Being.
Аниме-сериал «Sora wo Kakeru Shoujo» (Девочка, покорившая пространство) — в одной из земных точек Лагранжа расположена колония (обширный комплекс космических станций) Кирквуд, где родилась и жила главная героиня и большинство персонажей аниме. Какая именно из точек Лагранжа подразумевается — неизвестно; ещё одну, предположительно, занимает космическая колония Улле.

Видеоигрыправить

Touhou Project — в рассказе-приложении к официальному музыкальному альбому Torifune Iseki ~ Trojan Green Asteroid (действие всех рассказов-приложений к музыкальным альбомам, кроме первого, происходит в будущем) говорится о космической станции Торифунэ, на которой проводился эксперимент по созданию изолированной самодостаточной экосистемы. На станции произошла авария, и она, якобы, затерялась в космосе, но на самом деле для такого случая на ней была предусмотрена специальная система, которая отвела её в точку Лагранжа «Земля — Луна». Правда, в какую конкретно, не поясняется.
Prey — станция Талос-1, где происходит действие, находится в L2 между Землёй и Луной.

Подробное описание

L1

Чем ближе объект к солнцу (или к объектам, которые он окружает), тем быстрее он движется. Таким образом, спутники с орбитами меньше орбиты Земли рано или поздно достигнут Земли. Однако, если мы поместим его посередине, Гравитация Земли направлена в направлении, противоположном гравитации Солнца, что компенсирует часть солнечного толчка. заставляя его двигаться по орбите с меньшей скоростью. Если расстояние правильное, спутник будет двигаться достаточно медленно, чтобы сохранить свое положение между Землей и Солнцем. Это точка L1, которая будет использоваться для наблюдения за поверхностью Солнца, поскольку струи частиц оттуда достигают L1 за час до достижения нашей планеты.

L2

То же самое, что произошло с L1, происходит на другой стороне Земли, за пределами нашей орбиты. ИЛИПомещенный туда космический корабль будет дальше от Солнца, чем мы, и в конечном итоге отстанет., но на правильном расстоянии гравитационное влияние Солнца будет добавляться к гравитационному влиянию Земли, заставляя спутники вращаться вокруг Земли.

L3

L3 находится на дальней стороне Солнца, немного позади орбиты нашей планеты. Объекты в L3 невозможно наблюдать с Земли. Фактически, эта точка часто используется в научной фантастике для определения местоположения планет, которые находятся на одной орбите с нашей. Это менее стабильно, чем L1 или L2. Любое возмущение заставит космический корабль, спутник или зонд начать удаляться от него, что потребует постоянного использования двигателей, чтобы оставаться в нужном месте. В основном это происходит потому, что другие планеты находятся ближе к этой точке, чем наша планета. Например, Венера проходит около 50 000 000 км от точки L3 каждые 20 месяцев.

L4 и L5

Точки L4 и L5 расположены на 60 градусов впереди и позади Земли, если смотреть со стороны Солнца, близко к орбите Земли. В отличие от остальных, L4 и L5 очень устойчивы к любым гравитационным возмущениям. По этой причине пыль и материал астероидов имеют тенденцию накапливаться в этих областях.

Точки Лагранжа в науке[править]

Французский математик Жозеф Луи Лагранж, исследуя движение Луны вокруг Земли, вывел частные решения для так называемой задачи трёх тел. Кроме него, этой задачей занимался еще и Леонард Эйлер, но точки все же назвали в честь Лагранжа. А в общем виде эта задача не решена до сих пор.

Всего точек пять. Первые три из них называются коллинеарными и расположены на линии, проходящей через оба массивных тела. Точка L1 лежит между двумя телами системы, ближе к менее массивному телу, L2 — снаружи, за менее массивным телом и L3 — за более массивным. Эти точки являются точками неустойчивого равновесия — незначительного изменения внешних сил достаточно, чтобы тело покинуло точку равновесия и уже не вернулось в нее. Поэтому, к слову, Противоземля не может существовать — регулярно пролетающая мимо L3 Венера давным-давно спихнула бы Противоземлю с ее предположительного места.

Оставшиеся две точки, именуемые треугольными или троянскими (в честь троянских астероидов Юпитера, которые именно в этих точках и находятся, если посмотреть карту — видно что самые большие и плотные кучи астероидов сформированы в точках Лагранжа), расположены почти на орбите меньшего из двух массивных тел. Точнее, они располагаются в третьей вершине равностороннего треугольника, двумя другими углами которого являются центры масс двух тел, соответственно, на 60° вперёд (точка L4) и на 60° назад (точка L5). Эти точки являются точками устойчивого равновесия — тело, незначительно отклонившееся от точки, под воздействием гравитационных сил возвращается в нее. За это их и любят учёные и фантасты, возводящие в этих точках различные суперструктуры.

При строго определённой плэпорции массы двух тел (например, система двойник Солнца + коричневый карлик, обращающийся по орбите с низким эксцентриситетом) возможен даже такой феномен, как возникновение троянских планет. То есть, в L4, L5 или обеих сразу точках у карлика будет по планете размером с Землю. Если плэпорция не соблюдается, то троянская планета будет неустойчива, сойдёт со своего места и, возможно, тюкнет материнскую планету; ученые предполагают, что именно это произошло с Землёй в катархее (троянская планета Тэя столкнулась с Землёй, так как у Земли не хватило массы удерживать её на месте), и в результате этого столкновения образовалась Луна.

Кроме того точки Лагранжа используются для гравитационных манёвров называемых w:Межпланетная транспортная сеть. Особенностьей у этой сети две: во-первых ЧРЕЗВЫЧАЙНО низкие затраты энергии на отправку грузов. Фактически, вам достаточно рассчитать траекторию и дать Очень Тяжелому Грузу (помним астероид-метлу для проекта расчистки орбиты Земли от синдрома Кесслера?) легкого пендаля — и дальше груз попадет в место назначения без дополнительных маневров. Это был плюс. Теперь минус: это очень медленный вид транспортировки. Нет, это ОЧЕНЬ медленный способ транспортировки. Кто-то тут ныл что до Марса лететь полгода, а до Юпитера — семь лет? Вам повезёт если ваш груз доберётся до цели на орбите соседней планеты лет за десять. Но, с другой стороны, если у вас работает добыча полезных ништяков где-то у черта на рогах, грузы можно просто выстреливать по сети и забыть про них. Через N лет первые грузы начнут прибывать, а дальше их прибытие станет постоянным, и данный вопрос перестанет кого-либо волновать.

Четвертая и пятая точки Лагранжа

Четвертая и пятая точки Лагранжа называются треугольными. Если в системе, состоящей из двух массивных космических объектов, вращающихся вокруг общего центра масс, на основе линии, соединяющей эти объекты, мысленно начертить два равносторонних треугольника, вершины которого будут соответствовать положению двух массивных тел, то четвертая и пятая точки Лагранжа будут находиться в месте третьих вершин данных треугольников. То есть, они будут находиться в плоскости орбиты второго массивного объекта в 60 градусах сзади и впереди него.

Треугольные точки Лагранжа также называют еще и «троянскими». Второе название точек происходит от троянских астероидов Юпитера, которые являются ярчайшим наглядным проявлением четвертой и пятой точек Лагранжа в нашей Солнечной системе.

В данный момент четвертая и пятая точки Лагранжа в двойной системе Солнце-Земля никак не используются. В 2010 году в четвертой точке Лагранжа этой системы ученые обнаружили достаточно крупный астероид. В пятой точке Лагранжа на данном этапе никаких крупных космических объектов не наблюдается, однако последние данные говорят нам о том, что там находится большое скопление межпланетной пыли.

В 2009 году два космических аппарата STEREO пролетели через четвертую и пятую точки Лагранжа.
Точки Лагранжа часто используются в научно-фантастических произведениях. Часто в этих областях пространства, вокруг двойных систем, писатели-фантасты помещают свои вымышленные космические станции, мусорные свалки, астероиды и даже другие планеты.
В 2018 году во второй точке Лагранжа в двойной системе Солнце-Земля ученые планируют поместить космический телескоп «Джеймс Уэбб». Этот телескоп должен заменить действующий космический телескоп « », который находится в этой точке. В 2024 году ученые планируют поместить в этой точке еще один телескоп «PLATO».
Первая точка Лагранжа в системе Луна-Земля могла бы стать отличным местом для размещения пилотируемой орбитальной станции, которая могла бы значительно уменьшить затрату ресурсов, необходимых для того, чтобы добраться с Земли на Луну.
Два космических телескопа «Планк» и « », которые были запущены в космос в 2009 году, в данный момент находятся во второй точке Лагранжа в системе Солнце-Земля.

Какую бы цель вы перед собой не ставили, какую бы миссию не планировали — одним из самых больших препятствий на вашем пути в космосе будет топливо. Очевидно, что какое-то его количество нужно уже для того, чтобы покинуть Землю. Чем больше груза требуется вывести за пределы атмосферы, тем больше нужно горючего. Но из-за этого ракета становится ещё тяжелее, и всё это превращается в замкнутый круг. Именно это мешает нам отправлять несколько межпланетных станций по разным адресам на одной ракете — на ней просто не хватит места для топлива. Однако ещё в 80-х годах прошлого века учёные нашли лазейку — способ путешествовать по Солнечной системе, почти не используя горючее. Он называется «Межпланетная транспортная сеть».

Природные объекты в точках Лагранжа

Из-за естественной стабильности L 4 и L 5 естественные объекты часто встречаются вращаются вокруг точек Лагранжа планетных систем. Объекты, населяющие эти точки, обычно называются «троянами » или «троянскими астероидами». Название происходит от названий, которые были даны астероидам, обнаруженным на орбите вокруг Солнца — Юпитер L4и L 5 точек, которые были взяты из мифологических персонажей из Гомера Илиада, эпическая поэма, действие которой происходит во время Троянской войны. Астероиды в точке L 4, впереди Юпитера, названы в честь греческих букв в «Илиаде» и упоминаются как «греческий лагерь ». Те, которые находятся в точке L 5, названы в честь троянских символов и называются «лагерь троянцев ». Оба лагеря считаются разновидностями троянских тел.

Поскольку Солнце и Юпитер — два самых массивных объекта в Солнечной системе, троянских коней Солнце-Юпитер больше, чем для любой другой пары тел. Однако меньшее количество объектов известно в точках Лангрейдж других орбитальных систем:

Точки Солнце – Земля L 4 и L 5 содержат межпланетную пыль и по крайней мере один астероид., 2010 TK7.
Точки L 4 и L 5 Земля – Луна содержат концентрации межпланетной пыли, известной как облака Кордылевского.. Стабильность в этих конкретных точках сильно осложняется гравитационным влиянием Солнца.
Солнце — Нептун L4и L 5 точки содержат несколько десятков известных объектов, Нептун трояны.
Mars имеет четыре принятых трояна Mars : 5261 Eureka, 1999 UJ7, 1998 VF31 и 2007 NS2.
Несколько астероидов также вращаются вокруг точки L 3 Солнца – Юпитера, называемой семейством Хильды.
спутником Сатурна Тетис с двумя меньшими лунами в своем L 4 и L 5 точек, Telesto и Calypso. Другой спутник Сатурна, Диона, также имеет две лагранжевые коорбитали, Элен в точке L 4 и Полидевки в точке L. 5. Луны блуждают азимутально вокруг точек Лагранжа, при этом Полидевки описывают самые большие отклонения, перемещаясь на 32 ° от точки Сатурн – Диона L 5.
Один версия гипотезы гигантского удара постулирует, что объект с именем сформировался в точке L 4 или L 5 Солнце-Земля и разбился в Землю после того, как ее орбита дестабилизируется, образуя Луну.
В двойных звездах, полость Роша имеет вершину, расположенную на L 1 ; если одна из звезд расширяется за пределы своей полости Роша, то она теряет материю в пользу своей звезды-компаньона, известной как переполнение полости Роша.

Объекты, которые находятся на подковообразных орбитах иногда ошибочно называются троянами, но не занимают точки Лагранжа. Известные объекты на подковообразных орбитах включают 3753 Cruithne с Землей и спутники Сатурна Эпиметей и Янус.

Устойчивость точек Лагранжа.

Качественный контурный график эффективного потенциала V _eff (x ₃ , y ₃ ) для пробной массы 3 в системе планеты (Земля) и ее центральной звезды (Солнца) в общей плоскости через небесные тела.

Первые три точки Лагранжа устойчивы только в отношении отклонений, перпендикулярных соединительной линии между двумя большими телами, в то время как они нестабильны в отношении отклонений в направлении этой соединительной линии. Самый простой способ увидеть это — взглянуть на точку L ₁ . Сила действует обратно в точку равновесия на тестовую массу, которая удаляется из L ₁ по одной из красных стрелок, перпендикулярных соединительной линии (в направлении y: эффективная сила притяжения). Причина этого в том, что компоненты горизонтальной силы двух больших тел компенсируют друг друга, а компоненты вертикальной силы складываются. Если, с другой стороны, объект перемещается немного ближе к одному из двух других тел от точки L ₁ (синие стрелки!), Гравитационная сила тела, к которому он подошел, больше: следовательно, он перемещается от точки равновесия (по оси x: эффективная сила отталкивания). Объект ведет себя аналогично тому, как сфера ведет себя на седловой поверхности , более глубокие области которой указывают на два больших тела.

Точки L ₁ и L ₂ , следовательно , нестабильно, но все же полезно, так как небольшие корректирующие маневры космического зонда достаточны , чтобы держать их там. Без этого она бы отошла от этих точек.

В отличие от этого возможны стабильные орбиты вокруг L ₄ и L ₅ при условии, что соотношение масс двух больших тел больше 24,96. Если небольшое тело, расположенное в этих точках, слегка отклоняется, сила Кориолиса с точки зрения системы отсчета, в которой находятся точки Лагранжа, переводит его на орбиту в форме почки вокруг этой точки. Таким образом, он остается близким к этим точкам даже без корректирующих маневров.

Космические миссии в точках Лагранжа

SOHO (Солнечная гелиосферная обсерватория), Advanced Composition Explorer (ACE) и Global Geoscience WIND находятся на орбите вокруг Солнца-Земли L1, что обеспечивает постоянное и непрерывное наблюдение Солнца, делая его идеальным местом для изучения солнечной среды. В отличие от SOHO, солнечные обсерватории, ранее вращавшиеся вокруг Земли, прерывали свои наблюдения всякий раз, когда Земля затмевала Солнце, заслоняя поле зрения звезды.

(WMAP), который был развернут для определения условий в ранней Вселенной на основе данных, собранных о космическом микроволновом фоновом излучении, был расположен рядом с L2 Солнце-Земля (2001–2010 гг.), но вместо того, чтобы оставаться на L2, он следовал схеме Лиссажу.

Космический телескоп Джеймса Уэбба (JWST) в точке L2 Солнца-Земли и климатическая обсерватория глубокого космоса (DSCOVR) в точке L1 могут поддерживаться там с минимальным расходом топлива и незначительными корректировками. Некоторые другие космические обсерватории, такие как “Гершель” и “Планк” (для предельно точного измерения CMB), а также “Гайя” (для картирования положения и скоростей миллиарда звезд с целью изучения истории Млечного пути), также находятся на орбите Солнце-Земля L2.

В системе Солнце-Юпитер более 7 000 астероидов группируются вокруг гравитационно стабильных точек Лагранжа L4 и L5. Называемые троянцами, эти астероиды в целом сгруппированы в два роя – один предшествует газовому гиганту, а другой следует за ним по орбите вокруг Солнца.

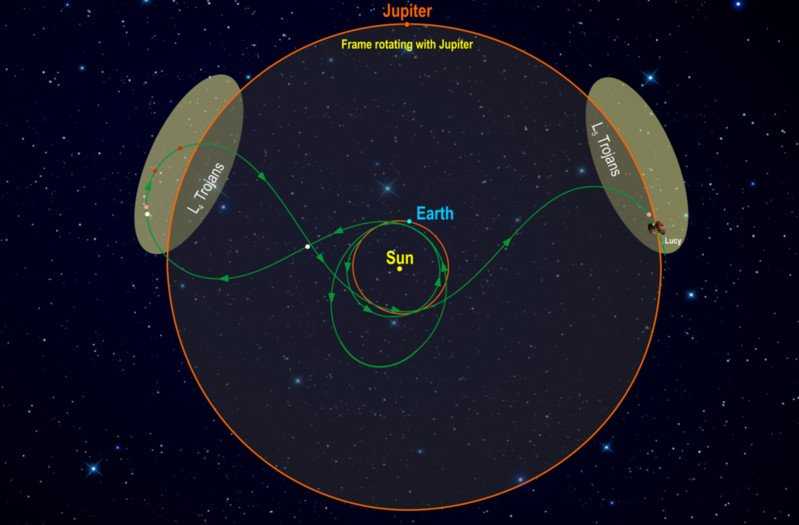Троянские астероиды системы Солнце-Юпитер в L4 и L5.

Ученые предположили, что области Лагранжа могут таить в себе еще не открытые планетные тела или даже обломки древних внеземных космических кораблей. Поскольку точки Лагранжа возникают в пространстве, где две или более противоположные силы уравновешены, если бы космический корабль мог генерировать силу, противодействующую гравитации, можно было бы создать искусственные точки равновесия в пространстве, чтобы космический корабль мог висеть практически в любой точке космоса без необходимости постоянно следовать по определенной орбите. Для этого можно было бы использовать солнечные паруса, использующие солнечный свет для движения.