Биография леонарда эйлера

Снова в Россию

Со времени отъезда Эйлера в России многое изменилось: наступила блестящая эпоха Екатерины Великой. Тем более что, как утверждал Фусс, родственник Эйлера, его неудержимо влекло в Россию. Однако Фридриху Великому не хотелось отпускать Эйлера в Петербург: он составлял славу академии и был очень полезен своим трудолюбием; король нехотя, но понемногу улучшал его материальное положение, а Эйлер, не имея веского предлога к отъезду в Россию, покорялся воле Фридриха и скрепя сердце оставался в Берлине.

Но в мае 1766 года русский посол в Берлине князь Долгорукий сообщил Эйлеру, что императрица Екатерина II, соглашаясь на любые условия, приглашает его снова приехать в Россию и занять «свое неотъемлемое место» в Академии наук. Эйлер едет в Петербург и наносит визит императрице, которая сразу же жалует ему восемь тысяч рублей серебром на покупку дома. Великий математик решает остаться.

Но едва ученый успел устроиться в Петербурге, его постигла болезнь, в результате которой он лишился второго глаза. Казалось, окончательная потеря зрения должна была лишить его возможности заниматься математикой. Но он как ни в чем не бывало продолжал свои труды, диктуя тексты, а его ученик Румовский переводил их на русский язык.

Эйлера продолжали преследовать несчастья. Внезапно дом его и большая часть имущества сгорели. Императрица Екатерина заботилась об Эйлере и на этот раз настояла на том, чтобы Эйлер пригласил лучшего окулиста того времени и подверг свой глаз операции. Само собой разумеется, что императрица дала ему необходимые на то средства. Эйлер пригласил барона Вентцеля, который снял с его глаза катаракту, и он снова увидел свет.

Но радость была непродолжительной. Несмотря на предостережение врача, Эйлер начал вновь усиленно работать и вторично лишился зрения.

Умер Эйлер 7 сентября 1783 года в возрасте 76 лет.

Петербургская академия наук облачилась в глубокий траур. Было решено, что мраморный бюст Эйлера всегда будет украшать собой зал, в котором происходят академические заседания.

Как писал французский философ и математик Кондорсе, Россия «подает пример цивилизованной Европе, как чествовать великих людей при жизни и уважать их память по смерти; и другим нациям приходится в данном случае краснеть, что они не только в этом отношении не могли предупредить Россию, но даже не в силах ей подражать».

ссылки

1. «Леонард Эйлер» в Википедии. Получено 20 февраля 2019 г. из Википедии: en.wikipedia.org
2. «Леонард Эйлер» в университете Гранады. Получено 20 февраля 2019 г. из Университета Гранады: ugr.es
3. «Загадка, разгаданная 300 лет назад математиком Леонардом Эйлером, который сегодня позволяет нам получить доступ к Интернету» на BBC London. Получено 20 февраля 2019 года с BBC — Новости — World: bbc.com
4. «Леонард Эйлер» в Британской энциклопедии. Получено 20 февраля 2019 г. из Британской энциклопедии: britannica.com
5. «Фразы Леонарда Эйлера» в фразах и мыслях. Получено 20 февраля 2019 г. с фраз и мыслей: frasesypensamientos.com.ar

Законы Кеплера

В 1609 году в Праге вышла из печати книга Кеплера «Новая астрономия» («Astronomia Nova»). В этой книге Кеплер излагает свои два
эмпирических закона, открытых прежде всего на основе изучения движения Марса и Земли.

Закон 1. Планеты обращаются вокруг Солнца по эллиптическим орбитам. При этом Солнце располагается
не в центре эллипса, а в одном из фокусов эллипса. Следовательно, расстояние планеты от Солнца не всегда одинаковое.

Закон
2. Радиус-вектор планеты (т.е. отрезок, соединяющий Солнце и планету) описывает равные площади за равные
промежутки времени. Этот закон указывает, что скорость движения планеты по её орбите непостоянна: при приближении к Солнцу планета движется быстрее, при
удалении от него — медленнее. Второй закон движения планет обычно называют законом площадей.

Закон 3. (Сформулирован в книге «Гармония мира» («Harmonice mundi»), опубликованной по частям в 1618-1621 гг.).
Квадраты периодов обращения любых двух планет относятся между собой как кубы их средних расстояний от Солнца.

Не все учёные — современники Кеплера восприняли его законы движения планет. Например, Галилей не признавал факт неравномерного движения планет. С течением
времени правильность законов Кеплера подтвердилась полностью. Работы Кеплера подготовили почву для открытия Ньютоном закона всемирного тяготения. До
настоящего времени законы Кеплера остаются основой небесной механики.

От дифуров до топологии

Эйлер создал как самостоятельную дисциплину теорию обыкновенных дифференциальных уравнений и заложил основы теории уравнений с частными производными. Здесь ему принадлежит большое число открытий. Например, выяснение основных свойств уравнения Риккати, интегрирование линейных уравнений с переменными коэффициентами с помощью бесконечных рядов, различные приближенные методы и ряд приемов решения уравнений с частными производными.

Эйлер высказал и подкрепил примерами убеждение в целесообразности применения расходящихся рядов и предложил методы обобщенного суммирования рядов, предвосхитив идеи современной строгой теории расходящихся рядов, созданной на рубеже XIX и XX веков. Он открыл так называемую формулу суммирования Эйлера—Маклорена, предложил преобразование рядов, носящее его имя и ввел в математику новые важные типы рядов (например, тригонометрические ряды).

По замечанию Пафнутия Чебышёва, Эйлер положил начало всем изысканиям, составляющим общую часть теории чисел. Так, он доказал ряд утверждений, высказанных Ферма (например, малую теорему Ферма). В работах о разбиении чисел на слагаемые и по теории простых чисел Эйлер впервые использовал методы анализа, став тем самым создателем аналитической теории чисел.

Научная карьера в Санкт-Петербурге

В 1727 г. Леонард Эйлер приехал в Санкт-Петербург, где стал адъюнктом высшей математики. Российское правительство выделило ему квартиру и определило оклад в размере 300 рублей в год.

Математик сразу же начал учить русский язык, который смог освоить в сжатые сроки.

Позднее Эйлер подружился с Кристианом Гольдбахом – постоянным секретарем академии. Она вели активную переписку, которая сегодня признана важным источником по истории науки в 18 веке.

Данный период биографии Леонарда был необычайно плодотворен. Благодаря своим трудам он быстро приобрел мировую известность и признание со стороны научного сообщества.

Политическая нестабильность в России, прогрессировавшая после смерти императрицы Анны Ивановны, вынудила ученого выехать из Санкт-Петербурга.

В 1741 г., по приглашению прусского монарха Фридриха 2, Леонард Эйлер вместе с семьей отправился в Берлин. Немецкий король хотел основать академию наук, поэтому был заинтересован в услугах ученого.

Детство и юность

Леонард Эйлер родился в Базеле, Швейцария 15 апреля 1707 года. Семья жила на скромный заработок отца, проповедника, увлеченного математикой. Он и стал первым учителем будущего ученого.

Мальчик получил начальное образование у репетитора священника Йоганесса Буркхарта, а в 1720 году поступил для дальнейшего обучения в Базельский университет. Юноша усердно учился и проявлял выдающиеся математические способности. Его старания были замечены почетным математиком Европы — Иоганом Бернулли и учеными мужами Российской Академии наук, от которых вскоре последовало приглашение работать в Санкт-Петербург.

Санкт-Петербург

17 мая 1727 г. Эйлер поступает на службу в медицинское отделение Императорской российской академии наук в Санкт-Петербурге, но почти сразу же переходит на математический факультет. Однако из-за волнений в России, 19 июня 1741 г. Эйлер переводится в Берлинскую академию. Там учёный прослужит около 25 лет, написав за это время более 380 научных статей. В 1755 г. его избирают иностранным членом Шведской королевской академии наук.

В начале 1760-х г.г. Эйлеру поступает предложение обучать наукам принцессу Анхальт-Дессау, которой учёный напишет более 200 писем, вошедших в ставший крайне популярным сборник «Письма Эйлера на разные предметы натуральной философии, адресованные немецкой принцессе».

Уникальность этого труда состояла ещё и в том, что в 1735 г. учёный почти полностью ослеп на правый глаз, а в 1766 г. левый его глаз был поражён катарактой. Но, даже несмотря на это, он продолжает свои работы и в 1755 г. пишет в среднем по одной математической статье в неделю.

В 1766 г. Эйлер принимает предложение вернуться в Петербургскую академию, и остаток своей жизни проведёт в России. Однако его второй приезд в эту страну оказывается для него не столь удачным: в 1771 г. пожар уничтожает его дом, а, вслед за этим, в 1773 г. он теряет свою жену Катарину.

На Берлин

Фридрих Великий был известен как просвещенный государь, покровитель философов и ученых. И он намеревался преобразовать Королевское общество, основанное по предложению Лейбница, в Академию наук. Именно с этой целью он и пригласил Эйлера, известного своей плодотворной деятельностью.

В 1744 году Фридрих Великий основал Берлинскую академию наук. И уже первые сборники трудов новой академии Эйлер украсил своими работами. Это не помешало ему, однако, не прерывать своей связи с Россией: авторство половины того, что печатала Петербургская академия наук, принадлежало Эйлеру. Он был поставлен директором математического отделения Берлинской академии и тотчас же ознаменовал это назначение, обнародовав свою теорию движений планет и комет. В том же году он получил премию от Французской академии наук за гипотезу, объясняющую явления магнетизма.

И в том же 1744-м Эйлер впервые корректно сформулировал механический принцип наименьшего действия и показал его первые применения. В своей монографии «Теория движения твердого тела» Эйлер разработал кинематику и динамику твердого тела и дал уравнения его вращения вокруг неподвижной точки, положив начало теории гироскопов. Разрабатывая теорию корабля, Эйлер внес ценный вклад в теорию устойчивости. Обширный цикл работ он посвятил математической физике: задачам о колебании струны, пластинки, мембраны и др.

 Уже первые сборники трудов Берлинской академии Эйлер украсил своими работами. Это не помешало ему, однако, не прерывать своей связи с Россией: авторство половины того, что печатала Петербургская академия наук, принадлежало Эйлеру

Все эти исследования стимулировали развитие теории дифференциальных уравнений, приближенных методов анализа, специальных функций, дифференциальной геометрии

Эти достижения Эйлера имеют не только важное теоретическое значение, они легли в основу ряда практических наук, таких как сопромат, теория машин и механизмов.. В оптике Эйлер дал формулу двояковыпуклой линзы, предложил способы устранения хроматических аберраций линз и дал методы расчета оптических узлов микроскопа.

В оптике Эйлер дал формулу двояковыпуклой линзы, предложил способы устранения хроматических аберраций линз и дал методы расчета оптических узлов микроскопа.

По поручению Фридриха II Эйлер перевел на немецкий язык «Новые принципы артиллерии» английского механика Бенджамена Робинса и дополнил книгу анализом движения снаряда в канале ствола орудия, а также учением о движении круглого снаряда в воздухе.

Из писем Фридриха к Эйлеру видно, что последнему часто приходилось заниматься применением математики на практике: ему поручали рассматривать различные финансовые проекты, наблюдать за тем, чтобы водяные насосы в Сан-Суси действовали правильно, проверять разные отчеты.

В 1749 году Фридрих поручил ему осмотреть канал Фуно между Гавелом и Одером и дать рекомендации по исправлению недостатков этого водного пути. Затем ему было поручено исправить водоснабжение в Сан-Суси.

Результатом этого стало более двадцати мемуаров по гидравлике, написанных Эйлером в разное время. Уравнения гидродинамики первого порядка с частными производными от проекций скорости, плотности к давлению называются гидродинамическими уравнениями Эйлера.

Несмотря на такие труды, вознаграждение Эйлера было вдвое меньше, чем, например, у известного французского математика Мопертюи, тоже члена Берлинской академии. Фридрих называл Эйлера своим одноглазым геометром, но находил, что Эйлер скучен, потому что слишком благочестив. Это привело к постепенному осложнению отношений между Эйлером и королем.

Между тем русская академия и русский двор никогда не переставали считать Эйлера своим, и то же относилось к русской армии. Когда русские войска в 1760 году в ходе Семилетней войны вступили в Берлин, дом Эйлера пострадал от русской артиллерии, но русское правительство тотчас же компенсировало ему потери с избытком.

Ферма Эйлера в Литцове, ныне Шарлоттенбург – часть Берлина; владения Эйлера отмечены латинской буквой “B”

Й. Брюнинг, Леонард Эйлер в Берлине

Сын крестьянина

Пьер Симон Лаплас родился 23 марта 1749 года в местечке Бомон-ан-Ож (Нормандия) в семье небогатого крестьянина. Пьер Симон окончил школу бенедиктинцев и был оставлен там же, в Бомоне, преподавателем математики военной школы. В семнадцать лет написал свою первую научную работу.

В 1766 году он отправился в Париж. Там он получил место преподавателя математики в Военной школе Парижа.. В 1773 году Лаплас становится адъюнктом, а в 1785 году действительным членом Парижской академии.

В 1784 году Лапласа сделали экзаменатором королевского корпуса артиллеристов. 8 мая 1790 году Национальное собрание Франции поручило Академии наук создать систему мер и весов “на все времена и для всех народов”. Председателем Палаты мер и весов был назначен Лаплас.

После народного восстания 1793 года во Франции установилась якобинская диктатура. 8 августа 1793 года декретом Конвента Академия наук в числе всех других королевских учреждений была упразднена, а Лаплас был уволен из Комиссии по мерам и весам. .

В 1795 году вместо Академии наук Конвент создал Национальный институт наук и искусств. Лаплас становится членом Института и возглавляет Бюро долгот, которое занималось измерением длины земного меридиана.

На другой день после переворота 18 брюмера Наполеон назначил Лапласа министром внутренних дел. В 1803 году Наполеон сделал Лапласа вице-президентом сената, а через месяц – канцлером. В 1804 году он получил орден Почетного легиона.

С 1801 по 1809 год Лаплас был избран членом королевских обществ в Турине и Копенгагене, академий наук в Геттингене, Берлине и Голландии. 13 октября 1802 году Лаплас стал почетным членом Петербургской академии наук.

“Аналитическая теория вероятностей” Лапласа издавалась трижды при жизни автора (в 1812, 1814, 1820 годы). Для разработки созданной им математической теории вероятностей Лаплас ввел так называемые производящие функции. Он привел полученные другими учеными результаты в стройную систему, упростил методы доказательства, для чего широко применял преобразование и доказал теорему об отклонении частоты появления события от его вероятности. Благодаря ему теория вероятностей приобрела законченный вид.

В физике Лаплас вывел формулу для скорости распространения звука в воздухе, создал ледяной калориметр, получил барометрическую формулу для вычисления изменения плотности воздуха с высотой, учитывающую его влажность. Он выполнил ряд работ по теории капиллярности и установил закон, который позволяет определить величину капиллярного давления и тем самым записать условия механического равновесия для подвижных (жидких) поверхностей раздела.

Первая его работа по небесной механике вышла в 1773 году. Она называлась “О причине всемирного тяготения и о вековых неравенствах планет, которые от него зависят”. В 1780 году Лаплас предложил новый способ вычисления орбит небесных тел.

Лаплас доказал устойчивость Солнечной системы. Он показал, что средняя скорость движения Луны зависит от эксцентриситета земной орбиты, а тот, в свою очередь, меняется под действием притяжения планет. По неравенствам движения Луны он определил величину сжатия Земли у полюсов.

Лаплас пришел к выводу, что кольцо Сатурна не может быть сплошным, иначе оно было бы неустойчивым; предсказал сжатие Сатурна у полюсов; установил законы движения спутников Юпитера. Полученные результаты были опубликованы Лапласом в его самом известном пятитомном классическом сочинении “Трактат о небесной механике” (1798-1825).

Космогоническая гипотеза Лапласа была опубликована в 1796 году в приложении к его книге “Наложение системы мира”. По ней, солнечная система образовалась из туманности, состоявшей из раскаленного газа и простиравшейся за пределы орбиты самой дальней планеты. Вращательное движение охлаждавшейся и сжимавшейся туманности обусловливало ее сплющивание. В процессе этого сплющивания возникала центробежная сила, под влиянием которой от туманности по ее краю отделялись кольца газовой материи, собравшиеся затем в комки и давшие начало планетам и их спутникам.

После реставрации монархии Лаплас пользовался благосклонностью Людовика XVIII. Король сделал его пэром Франции и пожаловал титул маркиза. В 1817 году Лаплас стал членом вновь созданной Французской академии, т.

е. одним из сорока бессмертных. Умер ученый после недолгой болезни 5 марта 1827 года.

Использованы материалы сайта http://100top.ru/encyclopedia/.

Карликовые планеты

Данные небесные тела отличаются своими маленькими размерами и удаленностью от Солнца. Эта группа объектов остается менее изученной из-за их расположения. Но с развитием техники у ученых появляется больше данных, имеющих большое значение в изучении космоса.

Плутон

Это одна из самых маленьких планет Солнечной системы, получившая в 2006 году статус «карликовая». Продолжительность ее вращения вокруг главной звезды — 248 лет, а оборот вокруг своей оси — 6,5 суток. Плутон расположен в поясе Койпера.

Несмотря на свои миниатюрные размеры, у него есть 5 спутников, самый известный из которых Харон. По своим габаритам он почти не уступает Плутону, поэтому их еще называют «двойной» планетой.

Поверхность Плутона состоит из камня и льдов, а атмосфера содержит большое количество углеводородных примесей, придающих планете коричневатый оттенок.

Церера

Долгое время считалась самым крупным астероидом, позже ей присвоили статус карликовой планеты. Но в своей группе по габаритам она занимает последнее место. Была обнаружена первой среди всех карликовых планет, в 1801 году. Находится Церера между Марсом и Юпитером.

Церера

Поверхность Цереры состоит из пород глинистого происхождения и кусков льда. Под коркой находится толстый ледяной слой и маленькое ядро. Разряженная атмосфера представляет собой водяной пар. Естественных спутников у Цереры нет.

Макемаке

Третья по величине среди карликовых планет, расположенная в поясе Койпера. Ученые ее открыли почти в одно время с Эридой. В отличие от остальных космических , была названа в честь богини изобилия, которой поклоняются племена с острова Пасхи.

Макемаке

Как и другие карликовые планеты, Макемаке пока еще мало изучена. Астрономам еще не удалось определить ее точные размеры. Но известна продолжительность года, которая равняется 306 земным годам. Поверхность карликовой планеты состоит из метанового льда и углеводородных смесей. Постоянной атмосферы у этой планеты нет. У Макемаке есть едва видимый спутник.

Эрида

По размерам не намного больше Плутона, но именно из-за нее последний потерял свой статус планеты. Эрида находится в поясе Койпера. Продолжительность вращения вокруг Солнца — 561 земной год.

Эрида была открыта в 2005 году, и астрономы были уверены, что обнаружили десятую планету. Но позже они отнесли ее к карликовым небесным телам.

Эрида

Эрида состоит из льдов и углеродных примесей, при испарении они образуют временную газовую оболочку. Она удалена от Солнца на 10 млрд. км, поэтому температура на ее поверхности не поднимается выше –253ºС.

Хаумеа

Это карликовая планета с самым быстрым вращением: один оборот вокруг своей оси занимает всего 4 часа, а вокруг Солнца — 282 года. Другое отличие Хаумеа от небесных тел Солнечной системы — неправильная сплюснутая форма, напоминающая яйцо. Эта планета была открыта одновременно с Эридой в 2005 году.

Хаумеа

Хаумеа выделяется среди карликовых планет наличием колец и малых небесных тел, образовавшихся в результате столкновения с крупным астероидом. Находится в поясе Койпера, а на ее перемещение незначительно влияет гравитация Нептуна. По своему составу Хаумеа — ледяной объект с минеральными и углеводородными примесями. Атмосферы эта карликовая планета не имеет.

Еще не все планеты Солнечной системы подробно изучены из-за их особенностей и удаленности. Но с развитием технологий удается получать новые данные, из-за которых приходится пересматривать устоявшиеся концепции. Возможно, в будущем появятся исследовательские аппараты, которые смогут собрать больше сведений о Венере, газовых гигантах и карликовых планетах.

Вклад в науку

Леонард Эйлер является ученым, чье творчество стало действительно достоянием всего человечества. Эйлером написано более 800 работ по самым разнообразным и сложнейшим вопросам из различных научных областей, в частности, математического анализа, дифференциальной геометрии, приближенных вычислений, теории чисел, небесной механики, математической физики, оптики, баллистики и др.

Эйлер стал первым ученым, кто в своих работах начал последовательно возводить «здание» анализа бесконечно малых величин. Исследования Эйлера в данной области были изложены в трилогии, которая включает:

1. «Введение в анализ»;
2. «Дифференциальное исчисление»;
3. «Интегральное исчисление».

После этого анализ бесконечно малых стал вполне оформившейся наукой, что является одним из самых глубоких научных достижений всего человечества.

Замечание 2

Кроме всего прочего, Эйлер оказал огромное влияние на развитие математического просвещения в XVIII в. в России. Под руководством Эйлера Петербургская математической школой, в которую входили академики С.Я. Румовский, С.К. Котельников, Н.И. Фусс, М.Е. Головин и др., была проведена значительная просветительная работа, создана обширная для своего времени учебная литература, а также выполнен ряд интересных исследований.

За все время существования в России Академии наук Эйлер считается одним из самых знаменитых членов данной академии.

Одной из главных задач, которая была поставлена перед Эйлером по прибытии в Россию, — подготовка научных кадров. Учениками Эйлера являются следующие ученые:

• М.Е. Головин (математика);
• Н.И. Фусс (математика);
• А.И. Лексель (астрономия, математика);
• С.К. Котельников (математика);
• П.Б. Иноходцев (астрономия);
• С.Я. Румовский (астрономия);
• С.К. Котельников (математика);
• И.А. Эйлер (математика).

Традиции Эйлера также оказали сильное влияние на учеников Чебышева, а именно: А.Н. Коркина, А.М. Ляпунова, Е.И. Золотарева и др.

Изучение Солнечной системы

Долгое время человечество было убеждено, что все звёзды и планеты вращаются вокруг Земли. Система мира с неподвижной Землёй в центре была разработана греческим учёным Птолемеем во 2 веке до нашей эры и просуществовала более полутора тысяч лет. 

В 1453 году польский астроном Николай Коперник доказал, что Земля, как и другие планеты (на тот момент их было известно шесть), вращаются вокруг Солнца. Однако вплоть до XVII века церковь считала это учение ересью и боролась с его последователями. 

Одним из них был итальянский монах Джордано Бруно. В 1584 году он опубликовал исследование, в котором утверждал, что Вселенная бесконечна, а Солнце подобно остальным звёздам, просто находится гораздо ближе к Земле. Бруно был схвачен инквизицией и приговорён к сожжению на костре как еретик. 

Другим последователем Коперника стал итальянский учёный Галилео Галилей. Он создал первый телескоп, который позволил увидеть кратеры Луны, пятна на Солнце, открыть четыре спутника Юпитера и установить, что планеты вращаются вокруг своей оси. Чтобы не повторить судьбу Бруно, Галилей был вынужден отречься от своих идей.

В XVII веке немецкий астроном Иоганн Кеплер открыл законы движения планет — ему удалось установить связь между скоростью вращения планеты и её расстоянием от Солнца. Его идеи воспринял знаменитый английский физик Исаак Ньютон, создатель теории всемирного тяготения. 

В XVIII—XIX веках открытия в области оптики позволили создать более мощные телескопы, которые позволили учёным узнать больше о солнечной системе. Были открыты планеты Уран и Нептун. 

В 1951 году Советский Союз вывел на орбиту Земли первый искусственный спутник. С этого момента началась Космическая эра — эпоха практического изучения солнечной системы. 

В 1961 году Юрий Гагарин стал первым человеком, побывавшем в космосе, а в 1969 году космический корабль «Аполлон-11» доставил людей на Луну. 

В 1970-х годах Советский Союз и США запустили несколько десятков аппаратов для исследования Марса, Венеры и Меркурия, а запущенные в 1980-х аппараты «Вояджер-1» и «Вояджер-2» позволили получить данные о дальних планетах — Юпитере, Сатурне, Уране, Нептуне и их спутниках. Большую роль в изучении солнечной системы сыграл вывод на орбиту Земли космического телескопа «Хаббл» в 1990 году. 

В нынешнем десятилетии космические агентства разных стран планируют пилотируемый полёт на Марс. Экспедиция на другую планету станет величайшим событием в истории освоения солнечной системы. И всё же пока человечество находится в самом начале пути изучения космоса.

Интересные факты

Эйлер создал большую часть математической терминологии и обозначений, которые всё ещё используются сегодня, особенно в математическом анализе.
Эйлера помнят как самого важного ученого XVIII века, а также как одного из величайших математиков, которые когда-либо жили.
Он также является одним из самых плодовитых учёных и мыслителей в области математики, поскольку его труды составляют от шестидесяти до восьмидесяти томов.
У Эйлера есть две цифры, названные его именем. Первое число — это число Эйлера в исчислении, представленное просто как «E», которое имеет приблизительное значение 71828

Второе число — это константа Эйлера-Маскерони, которую обозначают как «С». Она имеет приблизительное значение 0,57721.
Отец Эйлера был другом семьи Бернулли. В те годы Иоганн Бернулли считался самым выдающимся математиком Европы, и в конечном итоге он оказал самое большое воздействие на молодого Леонарда.
В 1726 году Эйлер завершил диссертацию о распространении звука под именем De Sono.
В области науки Эйлер много писал об идеях физики континуума, теории Луны и других областях.
В тригонометрии Леонард был первым исследователем, который ввёл письменную систему для тригонометрических функций с использованием буквы «E» в качестве основы.
Эйлер и его друг Даниил Бернулли были противниками монизма Лейбница и философии Христиана Вольфа.
Леонард настаивал на том, что знание основано частично на точных количественных законах, чего не могли обеспечить монизм и вольфовская наука.
Эйлер изображен на шестой серии швейцарских банкнот номиналом в 10 франков.
В 2002 году астероид был назван в его честь. Он был обнаружен 29 августа 1973 года советским астрономом Тамарой Смирновой.

Искусственное возникновение Луны

Эту нетрадиционную идею, далекую от науки, якобы выдвинули в 1960-х годах ученые Академии наук СССР Михаил Васин и Александр Щербаков. Они утверждали, что Луна — это искусственный объект, созданный не по воле природы.

Сегодня известно, что таких ученых в Академии наук в то время не существовало []. В 1968 году в «Комсомольской правде» была опубликована статья с названием «Луна — искусственный спутник?», но авторами ее были не академики, а журналисты. Впоследствии эта статья была переведена на английский язык и получила распространение за рубежом.

Подобные экзотические теории существовали на Западе еще со времен полета «Аполлона-12» на Луну в 1969 году []. С идеями «Луна — космический корабль пришельцев» связаны и убеждения в том, что внутри Луна якобы полая. Сейчас обе концепции — искусственной Луны и полой Луны, признаны антинаучными.

Вклад в астрономию

По возвращении в северную столицу России у Леонарда развилась катаракта в левом глазу, окончательно лишив ученого зрения. Эйлер обладал феноменальной памятью и не снизил интенсивность работ, даже после полной потери зрения. Он внес неоценимый вклад в развитие математики, механики, оптики, акустики и физической астрономии

Особое внимание, ученый уделял по сей день нерешенной проблеме взаимодействия нашей планеты с естественным спутником — Луной и центром системы — Солнцем. Его работы легли в основу таблиц, для расчетов долготы на морских путях кораблей

Эйлер выполнял в уме сложнейшие расчеты для второй теории движения Луны, после длительной слепоты продолжал разрабатывать теорию чисел и вывел закон квадратичной зависимости.

Работы Эйлера легли в основу таблиц, для расчетов долготы на морских путях кораблей

За свою жизнь, Эйлер посвятил астрономии более ста работ, основным направлением которых являлась небесная или «астрономическая» механика. Необходимость подробного изучения проблем в этом направлении, образовалась с потребностью определения положения мореходных судов, точность счета времени, а также интенсивности приливов и отливов. Еще одной причиной для исследований динамики космических объектов, стал вопрос о взаимодействии компонентов Солнечной системы и ее устойчивости. Еще Ньютоном были замечены отклонения в скорости движения планет и спутников, носящие вековые или годовые характеры. Эйлер точную четкую классификацию возмущений и посветил большую часть жизни решению этой проблемы астрономических механиков ХVІІІ века.

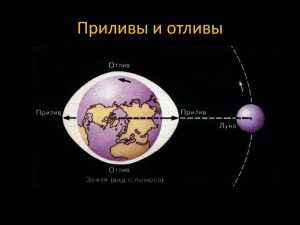
Леонард Эйлер разработал теорию о влиянии Луны на приливы и отливы

В 1740 году Леонард разработал теорию о влиянии Луны на приливы и отливы, за что был удостоен денежной награды Академии наук, обосновал принцип движения комет и других крупных объектов на основе Ньютоновских знаний о гравитации, разработал методику известную как метод четырех — пяти наблюдений, для определения конического сечения комет, и сформулировал уравнение для описания орбиты кометы. Астрофизику принадлежит и первая основополагающая теория «большого неравенства», описывающая движение Юпитера и Сатурна. Эйлер упростил точный расчет траектории динамики возмущенных тел, применив метод приближенного расчета, в последствии названого «Метод ломаных Эйлера». Большое количество задач, помог решить способ деления линейных уравнений на незначительные составляющие части последовательностей, где с уменьшением отдельных рядов и ростом их количества повышалась точность определения траектории небесного тела.