Законы иоганна кеплера

Законы движения планет вокруг Солнца

Сначала Кеплер установил, что планеты движутся вокруг Солнца по эллипсам и Солнце находится в одном из фокусов. Эллипс — это кривая, о которой знают все художники, потому что она представляет собой растянутый круг. Дети тоже знают о нем: им рассказывали, что если продеть в кольцо бечевку, закрепить ее концы и вставить в кольцо карандаш, то он опишет эллипс.

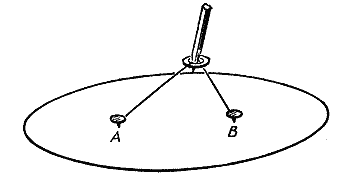
Две точки А и В — фокусы. Орбита планеты — эллипс. Солнце находится в одном из фокусов. Возникает другой вопрос: как движется планета по эллипсу? Идет ли она быстрее, когда находится ближе к Солнцу? Замедляет ли движение, удаляясь от него? Кеплер ответил и на этот вопрос. Он обнаружил, что если взять два положения планеты разделенных друг от друга определенным промежутком времени, скажем тремя неделями, потом взять другую часть орбиты и там — тоже два положения планеты разделенные тремя неделями, и провести линии (ученые называют их радиус-векторами) от Солнца к планете, то площадь заключенная между орбитой планеты и парой линий которые отделены друг от друга тремя неделями всюду одинакова, в любой части орбиты. А чтобы эти площади были одинаковы, планета должна идти быстрее, когда она ближе к Солнцу, и медленнее, когда она далеко от него.

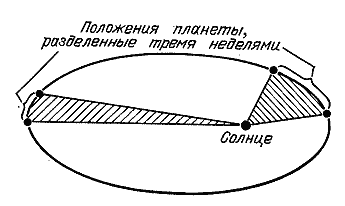
Еще через несколько лет Кеплер сформулировал третье правило, которое касалось, не движения одной планеты вокруг Солнца, а связывало движения различных планет друг с другом. Оно гласило, что время полного оборота планеты вокруг Солнца зависит от величины орбиты и пропорциорционально квадратному корню из куба этой величины. А величиной орбиты считается диаметр, пересекающий самое широкое место эллипса.

Так Кеплер открыл три закона, которые можно свести в один, если сказать, что орбита планеты представляет собой эллипс — за равные промежутки времени радиус-вектор планеты описывает равные площади и время (период) обращения планеты вокруг Солнца пропорционально величине орбиты в степени три вторых, т. е. квадратному корню из куба величины орбиты. Эти три закона Кеплера полностью описывают движение планет вокруг Солнца.

Тем временем Галилей открыл великий принцип инерции

. Затем наступила очередь Ньютона, который решил, что планете, вращающейся вокруг Солнца, не нужна сила, чтобы двигаться вперед; если бы никакой силы не было, планета летела бы по касательной. Но на самом деле планета летит не по прямой. Она все время оказывается не в том месте, куда попала бы, если бы летела свободно, а ближе к Солнцу. Другими словами, ее скорость, ее движение отклоняются в сторону Солнца.

Стало ясно, что источник этой силы (силы притяжения) находится где-то около Солнца.

Люди рассматривали в телескоп Юпитер со спутниками, обращающимися вокруг него, и им это напоминало маленькую Солнечную систему. Все выглядело так, будто спутники притягиваются к Юпитеру. Луна тоже вращается вокруг Земли и притягивается к ней точно таким же образом. Естественно, возникла мысль, что притяжение действует повсюду. Оставалось лишь обобщить эти наблюдения и сказать, что все тела притягивают друг друга. А значит, Земля должна притягивать Луну так же, как Солнце притягивает планеты. Но известно, что Земля притягивает и обычные предметы: вы, например, прочно сидите на стуле, хотя вам, может быть, и хотелось бы летать по воздуху. Тяготение предметов к Земле было явлением, хорошо известным. Ньютон предположил, что Луну на орбите удерживают те же силы, которые притягивают предметы к Земле.

Структура многогранников

Немецкий математик Иоганн Кеплер старался найти в природе повторяющиеся закономерности. Он жил на рубеже XVI и XVII веков, когда к астрологии относились очень серьезно, а астрономия пребывала в состоянии младенчества. Религиозные идеи представлялись такими же важными для выявления законов природы, как и наблюдения. Будучи мистиком, верившим, что основная структура вселенной построена на совершенных геометрических фигурах, Кеплер старался обнаружить в природе закономерности, связанные с правильными многогранниками.

Кеплер трудился через сто лет после того, как польский астроном Николай Коперник высказал предположение, что Солнце находится в центре вселенной, Земля же вращается вокруг него, а не наоборот. Со времен же древнегреческого философа Птолемея считалось, что Солнце и звезды вращаются вокруг Земли, двигаясь по поверхности твердых хрустальных сфер. Коперник не решился опубликовать свои радикальные идеи, пока был жив, и лишь перед самой смертью попросил коллегу сделать это. Предположение Коперника, что Земля не центр вселенной, — а из этого следовало, что и люди не самые главные в ней существа, опекаемые антропоцентрическим Богом, — взволновало многие умы.

Николай Коперник

Кеплер принял гелиоцентрическую концепцию Коперника, но сохранил веру в то, что планеты движутся вокруг Солнца по круговым орбитам. Он думал о системе, в которой орбиты планет лежат внутри вереницы вложенных одна в другую сфер, расстояния между которыми определяются математическими соотношениями, выведенными из размеров вписанных в эти сферы трехмерных геометрических фигур. Воображению его рисовались вписанные в сферы многогранники со все возрастающим числом граней. Основная идея состояла в том, что законы природы следуют основным геометрическим соотношениям, выведенным древними греками.

Слово «планета» происходит от греческого «блуждающая». Поскольку планеты нашей Солнечной системы находятся к Земле намного ближе, чем далекие звезды, они выглядят блуждающими по небу. Ночь за ночью планеты пролагают себе путь среди звезд. Однако время от времени путь каждой обращается вспять — планета описывает небольшую петлю. Такие ретроградные движения считались дурными знамениями. Птолемеева модель планетарного движения понять такое поведение планет не могла, и потому астрономы добавили к орбитам планет «эпициклы», или дополнительные петли. Но и эпициклы помогали плохо. Солнце-центричная модель вселенной Коперника требовала меньше эпициклов, чем земле-центричная, однако и она тонких деталей не описывала.

Пытаясь смоделировать орбиты планет так, чтобы они подтвердили его геометрические идеи, Кеплер использовал сложные таблицы движения планет, составленные Тихо Браге. И обнаружил в этих колонках цифр повторяющиеся закономерности, которые навели его на мысль о трех сформулированных им впоследствии законах.

Первый революционный прорыв Кеплера состоял в том, что он разобрался в ретроградном движении Марса. Кеплер понял, что попятные петли можно объяснить, если планеты вращаются вокруг Солнца по орбитам эллиптическим, а не круговым. Ирония состояла еще и в том, что из того вытекало: природа не следует совершенным геометрическим формам.

Гармония мира

Математическая красота Вселенной, о которой мечтал ученый, нашла неожиданное подтверждение: выяснилось, что соотношение большого и малого радиуса планет у всех планет Солнечной системы одинаково и совпадает с числом золотого сечения, погрешность составляет доли процента.

«Я выяснил, что все небесные движения, как в их целом, так и во всех отдельных случаях, проникнуты общей гармонией, правда, не той, которой я предполагал, но еще более совершенной», — писал о своих озарениях Кеплер. После его открытий представление о Земле как о центре Вселенной окончательно ушло из астрономии.

Несмотря на столь мощный вклад Иоганна Кеплера в развитие науки, его мать чуть было не сожгли на костре: в 1615 году она была обвинена в колдовстве, посажена на железную цепь в городских воротах и пять лет ожидала казни. Кеплеру пришлось лично защищать ее в суде, забросив астрономию, чтобы опровергнуть полсотни обвинений, в том числе связи с дьяволом, богохульство, порчу, некромантию и т. д. Мать удалось оправдать, но через полгода она умерла — в 1621 году. Кеплер прожил еще девять лет, успев выпустить свою завершающую книгу — «Гармония мира».

Вклад Кеплера в науку высоко оценил Альберт Эйнштейн. «Он жил в эпоху, когда еще не было уверенности в существовании некоторой общей закономерности для всех явлений природы, — писал автор теории относительности. — Какой глубокой была у него вера в такую закономерность, если, работая в одиночестве, никем не поддерживаемый и не понятый, он на протяжении многих десятков лет черпал в ней силы для трудного и кропотливого эмпирического исследования движения планет и математических законов этого движения! Сейчас, когда эти законы уже установлены, трудно себе представить, сколько изобретательности, воображения и неустанного, упорного труда потребовалось, чтобы установить эти законы и со столь огромной точностью выразить их».

Открытие новых небесных тел

Иоганн Кеплер открывает свои законы благодаря значительной работе по анализу астрономических наблюдений, установленных Тихо Браге, которые намного более точны, чем уже известные, он полагается, в частности, на положение Марса , движение которого он изучает с 1600 г. Он убежден. что Солнце, так или иначе, является «истинным» центром Солнечной системы (для внешних планет, таких как Марс, Коперник использует фиктивную точку около Солнца как центр круга, на котором с одинаковой скоростью вращается центр небольшой эпицикл, несущий планету). Руководствуясь этим убеждением и после долгих странствий, он в конце концов обнаружил, что движение планет имеет эллиптическую форму , причем Солнце находится в фокусе эллипса. Его результаты и способ, которым он к ним пришел, записаны в его главной работе, Astronomia nova , опубликованной в 1609 году, но фактически завершенной в конце 1605 года.

Его законы сами по себе позволили уточнить астрономические исследования и выявить нарушения в известных движениях тела с помощью поразительной прогрессии анализа.

Наиболее ярким примером является , что неровностей Урана , что позволило открытие Нептуна по Леверье ( 1811 г. — 1877 г. ), расчетным путем: открытие подтверждается наблюдением Галле ( — ) в 1846 году .

Кроме того, он смог определить, что звезда, появившаяся над яслями в день Рождества, была планетой Венера , особенно видимой в ту ночь. Таким образом, открытие Кеплера позволяет датировать это событие ночью с 24 на 25 декабря -8 года.

Тайна мироздания

Надо заметить, что астрономы конца XVI века еще не были уверены в том, как устроена Солнечная система, и разделялись на два лагеря: одни верили, что прав Птолемей и все планеты, Солнце, Луна и звезды вращаются вокруг неподвижной Земли. Другие же соглашались с Коперником и полагали, что именно Солнце является центром Вселенной, вокруг которого вращаются остальные небесные тела Солнечной системы. Около 1580 года датский астроном Тихо Браге выдвинул компромиссную версию: мол, все планеты, кроме Земли, вращаются вокруг Солнца, но Земля находится на особом положении — она неподвижно покоится в центре мира, заставляя крутиться вокруг себя Солнце и Луну. Так, геоцентрическая и гелиоцентрическая система мира объединились в гибридную геогелиоцентрическую. Но вопросы остались: как именно планеты вращаются, по какой траектории, с какой скоростью — этого точно никто не знал.

Как раз этими темами занялся Иоганн Кеплер. В 25 лет он написал книгу «Тайна мироздания» о шести известных тогда планетах — в ней он сопоставлял орбиты и «платоновы тела» и искал скрытую математическую гармонию Вселенной. Кеплер был настолько уверен в своей мистической теории, что тут же послал ее крупнейшим астрономам конца XVI века Галилео Галилею и Тихо Браге, и они хотя и отвергли фантазии юноши, но отметили его оригинальность и ум, а Галилей поддержал приверженность молодого ученого гелиоцентрической системе мира. После этого Кеплер вошел в научное сообщество и, осмелев, стал фонтанировать идеями. Одна из них совершенно не понравилась Галилею: молодой коллега утверждал, что Марс движется не по кругу, а по эллипсу. Известие о том, что все орбиты небесных тел — эллипсы, которое нам кажется аксиомой, не сразу было принято астрономами. Неравномерное движение Солнца, Луны и планет тогда объяснялось сложно: считалось, что планета равномерно движется по малому кругу, называемому эпициклом, центр которого, в свою очередь, движется по большому кругу, который называется деферентом.

«Я всегда ценил ум Кеплера — острый и свободный, пожалуй, даже слишком свободный, но способы мышления у нас совсем разные», — отзывался о Кеплере Галилей. А Тихо Браге пригласил молодого астронома к себе, и они десять лет плодотворно работали вместе. Следствием этого сотрудничества как раз и стали знаменитые три закона Кеплера.

История открытия

Вкратце история его такова. Еще древние, наблюдая за движением планет на небе, догадались, что все они, вместе с Землей, «ходят» вокруг Солнца. Позднее, когда люди забыли то, о чем знали прежде, это открытие заново сделал Коперник. И тогда возник новый вопрос: как именно планеты ходят вокруг Солнца, каково их движение? Ходят ли они по кругу и Солнце находится в центре или они движутся по какой-нибудь другой кривой? Как быстро они движутся? И так далее.

Выяснилось это не так скоро. После Коперника снова настали смутные времена и разгорелись великие споры о том, ходят ли планеты вместе с Землей вокруг Солнца или Земля находится в центре Вселенной. Тогда человек по имени Тихо Браге (Тихо Браге (1546-1601) — датский астроном)

придумал, как можно ответить на этот вопрос. Он решил, что нужно очень внимательно следить за тем, где появляются на небе планеты, точно это записывать и тогда уже выбирать между двумя враждебными теориями. Это и было началом современной науки, ключом к правильному пониманию природы — наблюдать за предметом, записывать все подробности и надеяться, что полученные таким способом сведения послужат основой для того или иного теоретического истолкования. И вот Тихо Браге, человек богатый, владевший островом поблизости от Копенгагена, оборудовал свой остров большими бронзовыми кругами и специальными наблюдательными пунктами и записывал ночь за ночью положения планет. Лишь ценой такого тяжелого труда достается нам любое открытие.

Когда все эти данные были собраны, они попали в руки Кеплера (Иоганн Кеплер (1571-1630) -немецкий астроном и математик, был помощником Браге)

, который и пытался решить, как движутся планеты вокруг Солнца. Он искал решение методом проб и ошибок. Однажды ему показалось, что он уже получил ответ: он решил, что планеты движутся по кругу, но Солнце лежит не в центре. Потом Кеплер заметил, что одна из планет, кажется Марс, отклоняется от нужного положения на 8 угловых минут, и понял, что полученный им ответ неверен, так как Тихо Браге не мог допустить такую большую ошибку. Полагаясь на точность наблюдений, он решил пересмотреть свою теорию и в конце концов обнаружил три факта.

Применение законов Кеплера

Пусть два тела с массами M и m находятся на расстоянии R друг от друга. Тогда энергия их взаимодействия равна

Полная энергия

Если тело находится в гравитационном поле и имеет некоторую скорость, то его полная энергия равна

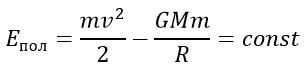
Таким образом, в соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.

Теорема вириала

В случае кругового движения кинети­ческая энергия в 2 раза меньше по модулю потенциальной. Поэтому

2E_к+E_п= 0

Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела.

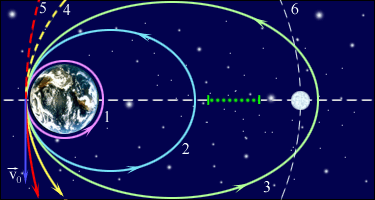
При  E_пол < 0  тело не может удалиться от центра притяжения на расстояние  r < r_max . В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы). Система с отрицательной полной энергией называется гравитационно связанной.

При  E_пол = 0  тело движется по параболической траектории. Скорость тела на бесконечности равна нулю.

При  E_пол > 0  движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии.

Первая космическая скорость

Это скорость движения по круговой траектории вблизи поверхности Земли

Это минимальная скорость, которую нужно сообщить телу, чтобы оно преодолело притяжение Земли и стало спутником. Для Земли примерно 7,9 км/с.

Вторая космическая скорость

Это скорость движения по параболической траектории

Она равна минимальной скорости, которую нужно сообщить телу на поверхности Земли, чтобы оно, преодолев земное притяжение, стало искусственным спутником Солнца. Находится из условия равенства нулю полной энергии системы. Для Земли примерно 11,2 км/с.

Третья космическая скорость

Это скорость, при которой тело преодолевает притяжение Солнца

где v – орбитальная скорость планеты, v₂ – вторая космическая скорость для планеты. Для Земли примерно 16,6 км/с.

Задачи:

Звезда и планета обращаются вокруг общего неподвижного центра масс по круговым орбитам. Найдите массу планеты m, если известно, что скорость движения планеты равна v₁, а скорость движения и период обращения звезды равны v₂ и T соответственно.

Если бы все линейные размеры Солнечной системы были пропорционально сокращены так, чтобы среднее расстояние между Солнцем и Землей стало 1 м, то какова была бы продолжительность одного года? Считайте, что плотность небесных тел при этом не меняется.

Автоматическая станция обращается вокруг планеты Марс с периодом T = 18 ч. Максимальное удаление от поверхности Марса (в апоцентре) a = 25000 км, минимальное (в перицентре) p = 1380 км. По указанным параметрам орбиты станции определите отношение массы Марса к массе Земли. Радиус Марса r_м = 3400 км, радиус Земли r_з = 6400 км.

Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты 422 тыс. км.

Вычислить параболическую скорость на поверхности Луны, R_Л = 0.27 радиуса Земли, M_Л = 1/81 массы Земли.

http://ency.info/earth/etapi-astronomii/16-zakon

http://www.afportal.ru/taxonomy/term/128

Как применяют законы Кеплера

Законы движения планет в астрономии происходят по законам Кеплера. В них учёный даёт объяснение и определение неоднородного перемещения космических тел. Кроме того, благодаря этим законам стало возможным установление положения объектов. Более того, с их помощью можно рассчитать массу тел.

Интересно, что планеты Солнечной системы в большинстве имеют орбиты, приближенные к окружности. Хотя особая выпуклость характерна для Марса и Плутона.

Орбиты планет Солнечной системы

Очевидно, что законы движения планет равносильны правилам движения спутников. Кстати, даже искусственных. То есть то, что мы запускаем в космос движется по этим самым принципам.

Можно сделать вывод, что благодаря обладанию знаний о закономерностях движения, стал возможным запуск космических ракет. А значит, сделан огромный шаг в направлении изучения Вселенной.

Безусловно, Кеплер внёс огромный вклад в астрономию. Его во всех смыслах можно назвать удивительным человеком. В то время, когда он жил никто не представлял Вселенную так, как он. Более того, сам он писал о себе: Этому человеку на роду написано проводить время за решением трудных задач, отпугивающих других.

И ведь действительно, благодаря его труду сформировалась планетарная астрономия. Можно сказать, открылось окно во Вселенную. Где, то что мы видим, мы можем измерить.

Однако, изначально было опубликовано только два закона. Позднее, спустя десять лет, общественности стал доступен третий закон Кеплера.

Астрономия

Разумеется, не все догадки учёных умов верны. Но свой вклад они определённо внесли. Мы уже говорили о том, что за все время изучения астрономии было сделано множество важных открытий. Сегодня, я думаю, мы в очередной раз рассмотрели и убедились в этом.

Первый закон Кеплера (закон эллипсов)[]

Файл:Kepler1.gif

Первый закон Кеплера.

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

Форма эллипса и степень его сходства с окружностью характеризуется отношением e=ca{\displaystyle e={\frac {c}{a}}}, где c{\displaystyle c} — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a{\displaystyle {a}} — большая полуось. Величина e{\displaystyle e} называется эксцентриситетом эллипса. При c={\displaystyle c=0} и e={\displaystyle e=0} эллипс превращается в окружность.

Доказательство первого закона Кеплера   

Закон всемирного тяготения Ньютона гласит, что «каждый объект во вселенной притягивает каждый другой объект по линии соединяющей центры масс объектов, пропорционально массе каждого объекта, и обратно пропорционально квадрату расстояния между объектами». Это предполагает, что ускорение a имеет форму

a=d2rdt2=f(r)r^.{\displaystyle \mathbf {a} ={\frac {d^{2}\mathbf {r} }{dt^{2}}}=f(r){\hat {\mathbf {r} }}.}

Вспомним, что в полярных координатах

drdt=r˙r^+rθ˙θ^,{\displaystyle {\frac {d\mathbf {r} }{dt}}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\theta }}{\hat {\boldsymbol {\theta }}},}

d2rdt2=(r¨−rθ˙2)r^+(rθ¨+2r˙θ˙)θ^.{\displaystyle {\frac {d^{2}\mathbf {r} }{dt^{2}}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}.}

В координатной форме запишем

r¨−rθ˙2=f(r),{\displaystyle {\ddot {r}}-r{\dot {\theta }}^{2}=f(r),}

rθ¨+2r˙θ˙={\displaystyle r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}=0.}

Подставляя θ¨{\displaystyle {\ddot {\theta }}} и r˙{\displaystyle {\dot {r}}} во второе уравнение, получим

rdθ˙dt+2drdtθ˙=,{\displaystyle r{d{\dot {\theta }} \over dt}+2{dr \over dt}{\dot {\theta }}=0,}

которое упрощается

dθ˙θ˙=−2drr.{\displaystyle {\frac {d{\dot {\theta }}}{\dot {\theta }}}=-2{\frac {dr}{r}}.}

После интегрирования запишем выражение

ln⁡θ˙=−2ln⁡r+ln⁡ℓ,{\displaystyle \ln {\dot {\theta }}=-2\ln r+\ln \ell ,}

ln⁡ℓ=ln⁡r2+ln⁡θ˙,{\displaystyle \ln \ell =\ln r^{2}+\ln {\dot {\theta }},}

ℓ=r2θ˙,{\displaystyle \ell =r^{2}{\dot {\theta }},}

для некоторой константы ℓ{\displaystyle \ell }, которая является удельным угловым моментом (ℓ=r×v{\displaystyle \ell =\mathbf {r} \times \mathbf {v} }).Пусть

r=1u,{\displaystyle r={\frac {1}{u}},}

r˙=−1u2u˙=−1u2dθdtdudθ=−ℓdudθ,{\displaystyle {\dot {r}}=-{\frac {1}{u^{2}}}{\dot {u}}=-{\frac {1}{u^{2}}}{\frac {d\theta }{dt}}{\frac {du}{d\theta }}=-\ell {\frac {du}{d\theta }},}

r¨=−ℓddtdudθ=−ℓθ˙d2udθ2=−ℓ2u2d2udθ2.{\displaystyle {\ddot {r}}=-\ell {\frac {d}{dt}}{\frac {du}{d\theta }}=-\ell {\dot {\theta }}{\frac {d^{2}u}{d\theta ^{2}}}=-\ell ^{2}u^{2}{\frac {d^{2}u}{d\theta ^{2}}}.}

Уравнение движения в направлении r^{\displaystyle {\hat {\mathbf {r} }}} становится равным

d2udθ2+u=−1ℓ2u2f(1u).{\displaystyle {\frac {d^{2}u}{d\theta ^{2}}}+u=-{\frac {1}{\ell ^{2}u^{2}}}f\left({\frac {1}{u}}\right).}

Закон всемирного тяготения Ньютона связывает силу на единицу массы с расстоянием как

f(1u)=f(r)=−GMr2=−GMu2{\displaystyle f\left({1 \over u}\right)=f(r)=-\,{GM \over r^{2}}=-GMu^{2}}

где G — универсальная гравитационная константа и M — масса звезды.

В результате

d2udθ2+u=GMℓ2.{\displaystyle {\frac {d^{2}u}{d\theta ^{2}}}+u={\frac {GM}{\ell ^{2}}}.}

Это дифференциальное уравнение имеет общее решение:

u=GMℓ21+ecos⁡(θ−θ).{\displaystyle u={\frac {GM}{\ell ^{2}}}\left.}

для произвольных констант интегрирования e и θ.

Заменяя u на 1/r и полагая θ = 0, получим:

r=1u=ℓ2GM1+ecos⁡θ.{\displaystyle r={1 \over u}={\frac {\ell ^{2}/GM}{1+e\cos \theta }}.}

Мы получили уравнение конического сечения с эксцентриситетом e и началом системы координат в одном из фокусов. Таким образом, первый закон Кеплера прямо следует из закона всемирного тяготения Ньютона и второго закона Ньютона.

Законы движения планет

Подробности

Обновлено 20.07.2018 19:28

Просмотров: 862

В конце XVI в. датский астроном И. Кеплер, изучая движение планет, открыл три закона их движения. На основании этих законов И. Ньютон вывел формулу для закона всемирного тяготения. В дальнейшем, используя законы механики, И. Ньютон решил задачу двух тел — вывел законы, по которым одно тело движется в поле тяготения другого тела. Он получил три обобщенных закона Кеплера.

Первый закон Кеплера
Под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе.

Планеты движутся вокруг Солнца по эллиптической орбите (рис. 15.6). Ближайшая к Солнцу точка орбиты называется перигелием, самая далекая — афелием. Линия, соединяющая какую-либо точку эллипса с фокусом, называется радиус-вектором.

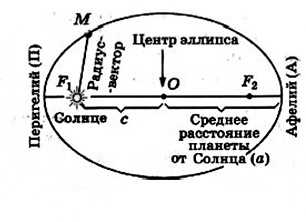
Отношение расстояния между фокусами к большой оси (к наибольшему диаметру) называется эксцентриситетом е. Эллипс тем сильнее вытянут, чем больше его эксцентриситет. Большая полуось эллипса а — среднее расстояние планеты до Солнца.

По эллиптическим орбитам движутся и кометы и астероиды. У окружности е = 0, у эллипса 0 < е < 1, у параболы е = 1, у гиперболы е > 1.

Движение естественных и искусственных спутников вокруг планет, движение одной звезды вокруг другой в двойной системе также подчиняются этому первому обобщенному закону Кеплера.

Второй закон Кеплера
Каждая планета движется так, что радиус-вектор планеты за равные промежутки времени описывает равные площади.

Планета проходит путь от точки А до А’ и от В до В’ за одно и то же время.

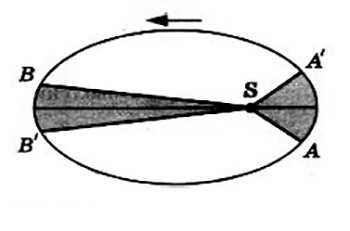
Другими словами, планета движется быстрее всего в перигелии, а медленнее всего — когда находится на наибольшем удалении (в афелии). Таким образом, второй закон Кеплера определяет скорость движения планеты. Она тем больше, чем планета ближе к Солнцу. Так, скорость кометы Галлея в перигелии равна 55 км/с, а в афелии 0,9 км/с.

Третий закон Кеплера
Куб большой полуоси орбиты тела, деленный на квадрат периода его обращения и на сумму масс тел, есть величина постоянная.

Если Т — период обращения одного тела вокруг другого тела на среднем расстоянии а, то третий обобщенный закон Кеплера записывается как

а3/[Т2 (М₁ + М₂)] = G/4π2

где М₁ и М₂ — массы притягивающихся двух тел, a G — гравитационная постоянная. Для Солнечной системы масса Солнца массы любой планеты, и тогда

Правая часть уравнения — постоянная для всех тел Солнечной системы, что и утверждает третий закон Кеплера, полученный ученым из наблюдений.

Третий обобщенный закон Кеплера позволяет определять массы планет по движению их спутников, а массы двойных звезд — по элементам их орбит.

Движение планет и других небесных тел вокруг Солнца под действием силы тяготения происходит по трем законам Кеплера. Эти законы позволяют рассчитывать положения планет и определять их массы по движению спутников вокруг них.

Следующая страница «Система Земля-Луна»

Назад в раздел «Астроноия -конспекты»

Астрономия. 11 класс — Конспекты по учебнику «Физика-11» (Мякишев, Буховцев, Чаругин) — Класс!ная физика

Видимые движения небесных тел —
Законы движения планет —
Система Земля—Луна —
Физическая природа планет и малых тел солнечной системы —
Солнце —
Основные характеристики звезд —
Внутреннее строение Солнца и звезд главной последовательности. Эволюция звезд —
Млечный Путь — наша Галактика —
Галактики —
Строение и эволюция Вселенной —
Кратко о солнечной системе и строении Вселенной

Закон притяжения

Притяжение небесных тел изучались многими учёными, но впервые научно были обоснованы, доказаны путём математических расчётов английским ученым в 17 веке Ньютоном. Он доказал прямую взаимосвязь между движением планет и тяготением. Открытия Ньютона были самыми популярными в науке более двух столетий до создания теории относительности.

Формула

Формула Закона притяжения имеет вид:

где M и m – массы Солнца и планеты, r – расстояние между ними, а постоянная сила гравитации \[\mathrm{G}=6,67 \times 10^{-11} \mathrm{Hм}^{2} / \mathrm{кг}^{2}\]

Ньютон – первый исследователь, который сделал важнейший вывод, что именно от сил притяжения зависит характер движения тел во Вселенной.

Ньютонова форма третьего закона Кеплера

Исаак Ньютон понял связь между законами классической механики и третьим законом Кеплера. Он вывел следующую формулу:

Т2знак равно4π2грамм(M+м)в3{\ displaystyle T ^ {2} = {\ frac {4 \ pi ^ {2}} {G (M + m)}} a ^ {3}}, чаще в виде Т2в3знак равно4π2грамм(M+м){\ displaystyle {\ frac {T ^ {2}} {a ^ {3}}} = {\ frac {4 \ pi ^ {2}} {G (M + m)}}}

или же :

• Т{\ displaystyle T}это период вращения объекта,
• в{\ displaystyle a}- большая полуось эллиптической траектории,
• грамм{\ displaystyle G}является постоянная всемирного тяготения ,
• м{\ displaystyle m} масса планеты,
• M{\ displaystyle M} масса звезды.

В случае системы звезда / планета массой планеты можно пренебречь по сравнению с массой звезды:
м{\ displaystyle m}M{\ displaystyle M}

Т2в3знак равно4π2грамм(M+м)≈4π2граммM{\ displaystyle {\ frac {T ^ {2}} {a ^ {3}}} = {\ frac {4 \ pi ^ {2}} {G (M + m)}} \ приблизительно {\ frac {4 \ pi ^ {2}} {GM}}}

Демонстрация

Начнем с установления закона площадей:

Либо .L→знак равнор→∧р→˙{\ Displaystyle {\ vec {L}} = {\ vec {r}} \ клин {\ точка {\ vec {r}}}}

У нас есть .ddтL→знак равнор→˙∧р→˙+р→∧р→¨знак равно→{\ displaystyle {\ frac {d} {dt}} {\ vec {L}} = {\ dot {\ vec {r}}} \ wedge {\ dot {\ vec {r}}} + {\ vec { r}} \ wedge {\ ddot {\ vec {r}}} = {\ vec {0}}}

Итак .L→знак равнорер→∧(р˙ер→+рθ˙еθ→)знак равнор2θ˙еz→знак равноПРОТИВте.еz→знак равноΛеz→{\ displaystyle {\ vec {L}} = r {\ vec {e_ {r}}} \ wedge ({\ dot {r}} {\ vec {e_ {r}}} + r {\ dot {\ theta) }} {\ vec {e _ {\ theta}}}) = r ^ {2} {\ dot {\ theta}} {\ vec {e_ {z}}} = Cte. {\ vec {e_ {z} }} = \ Lambda {\ vec {e_ {z}}}}

Пусть будет площадь, охватываемая вектором в течение и изменение в течение одного и того же времени.dS{\ displaystyle dS}р→{\ displaystyle {\ vec {r}}}dт{\ displaystyle dt}dр→{\ displaystyle {\ vec {dr}}}р→{\ displaystyle {\ vec {r}}}

Мы получили где .dSзнак равно12‖р→∧dр→‖знак равно12р2θ˙dтзнак равно12Λdт{\ displaystyle dS = {\ frac {1} {2}} \ left \ | {\ vec {r}} \ wedge {\ vec {dr}} \ right \ | = {\ frac {1} {2}} r ^ {2} {\ dot {\ theta}} dt = {\ frac {1} {2}} \ Lambda dt}S(т)знак равноΛт2{\ Displaystyle S (t) = {\ гидроразрыва {\ Lambda t} {2}}}

Мы делаем вывод, что площадь эллипса равна .πв21-е2{\ displaystyle \ pi a ^ {2} {\ sqrt {1-e ^ {2}}}}12ΛТзнак равноπв21-е2{\ displaystyle {\ frac {1} {2}} \ Lambda T = \ pi a ^ {2} {\ sqrt {1-e ^ {2}}}}

Вдобавок у нас есть .р(θ)знак равноΛ2граммM(1+епотому что⁡θ)⇒2взнак равнормянет+рмвИксзнак равно2Λ2граммM(1-е2){\ displaystyle r (\ theta) = {\ frac {\ Lambda ^ {2}} {GM (1 + e \ cos \ theta)}} \ Rightarrow 2a = r_ {min} + r_ {max} = {\ frac {2 \ Lambda ^ {2}} {GM (1-е ^ {2})}}}

Мы выводим это откуда, возводя в квадрат .12Тзнак равноπв32граммM{\ displaystyle {\ frac {1} {2}} T = {\ frac {\ pi a ^ {3/2}} {\ sqrt {GM}}}}Т2знак равно4π2граммMв3{\ displaystyle T ^ {2} = {\ frac {4 \ pi ^ {2}} {GM}} a ^ {3}}