Насколько близко может находиться Луна?
В сравнении другими космическими объектами Луна находится очень близко к нам, но я бы хотел, чтобы она была ещё ближе. Настолько близко, чтобы я смог увидеть мельчайшие детали на её поверхности без телескопа или бинокля.
Конечно, такая близость повлекла бы за собой ужасные проблемы. Например, интенсивные приливы, полное отсутствие хороших тёмных ночей для наблюдения звездопадов, и что-то ещё… ах да, полное уничтожение жизни на Земле. Пожалуй, я передумал, Луне лучше оставаться там, где она есть.
Среднее расстояние до нашего спутника составляет 384 467 километров. Я говорю “среднее”, потому что Луна на самом деле движется по эллиптической орбите. В ближайшей точке, расстояние составляет всего лишь 363 104 километров, а в самой дальней – 405 696 километров.
Таким образом, свету, путешествующему со скоростью 300 000 км/c, понадобится чуть более секунды, чтобы достичь нашего спутника. Луна очень далеко.
Но что случится, если Луна будет находиться гораздо ближе? Насколько близко она может располагаться и при этом всё ещё оставаться нашим спутником?
Опять же, я должен напомнить вам, что это чисто теоретические рассуждения. Луна не приближается к нам, а наоборот – она медленно удаляется от нас почти на 4 сантиметра в год.
Давайте вернёмся в прошлое, на миллиарды лет назад, когда молодая Земля столкнулась с объектом размером с Марс. Это катастрофическое столкновение выбросило огромное количество материала на орбиту нашей планеты. Со временем под действием гравитации из этого материала и сформировалась Луна, которую мы видим сегодня.
Вскоре после своего формирования, Луна была намного ближе, а Земля вращалась быстрее. В то время продолжительность дня на Земле не превышала 6 часов, а Луна совершала один оборот вокруг Земли всего за 17 суток.
Сила тяжести Земли остановила вращение Луны, а сила тяжести Луны постепенно замедлила вращение Земли. Таким образом, для сохранения общего углового момента системы, Луна должна постоянно отдалятся от нас.
Но если вы рассмотрите другой сценарий, в котором Луна вращается быстрее, чем планета, то Луна должна будет приближаться к нам. И это не приведёт ни к чему хорошему.
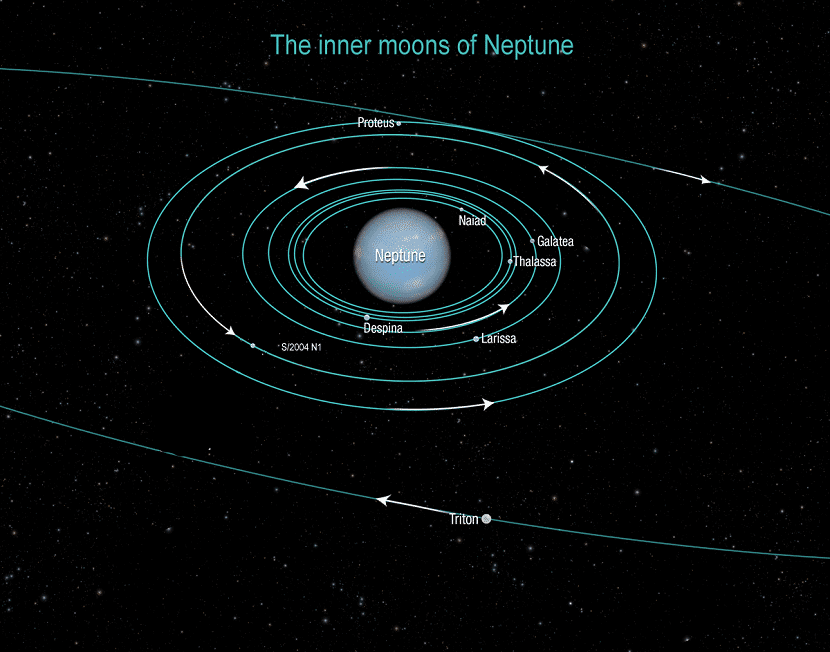
Для любых гравитационных взаимодействий существует критическая точка, которая называется предел Роша. Предел Роша – это точка, в которой объект, удерживаемый силой тяжести, подходит настолько близко к другому небесному телу, что оно начинает разрушаться.
Предел Роша определяется массами, размерами и плотностями двух объектов. Например, предел Роша для Земли и Луны составляет около 9 500 километров, при условии, что Луна является твёрдым шаром. Другими словами, если расстояние до Луны составит 9 500 километров или около того, то гравитация Земли разорвёт наш спутник.
Всё что останется от Луны – это кольцо мелких объектов, вращающихся вокруг нашей планеты. С течением времени все эти мелкие объекты упадут на Землю и это будут очень плохие дни для всего живого на Земле.
Но вы можете не волноваться, этого никогда не случится с Землёй, но возможно вы удивитесь узнав, что это произойдёт с Марсом. Его самый большой спутник Фобос вращается быстрее, чем планета, а это значит, что через несколько миллионов лет, он пересечёт предел Роша и будет разорван своей планетой на куски.
И ещё один момент. Прочитав эту статью, у вас может возникнуть следующий вопрос: ведь я тоже отдельный объект, и я нахожусь ближе, чем предел Роша, так почему меня всё ещё не разорвало?
На самом деле сила тяжести, удерживающая вас на поверхности, очень незначительна по сравнению с химическими связями, которые обусловливают устойчивость молекул, из которых вы состоите. Именно поэтому физики считают силу гравитации довольно слабой силой по сравнению со всеми другими силами Вселенной. Только гравитационные силы чёрной дыры смогут нарушить ваши химические связи и разорвать вас на части.
Итак, минимальное расстояние на котором Луна останется Луной составляет примерно 9 500 километров, в противном случае наш единственный спутник разрушится и погубит всё живое на Земле.
Пределы Роша для «жёсткого» и «жидкого» спутников[править | править код]
В приближении «жёсткого» сферического спутника, то есть при условиях пренебрежения его приливной деформацией и вращением, предел Роша aR{\displaystyle a_{R}} зависит от радиуса центрального тела R{\displaystyle R} и отношения плотностей центрального тела ρM{\displaystyle \rho _{M}} и спутника ρm{\displaystyle \rho _{m}}:
- aR=R(2ρMρm)13≈1,26R(ρMρm)13.{\displaystyle a_{R}=R\left(2\,{\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}\approx 1{,}26\,R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}.}
В приближении «жидкого» несферического спутника, форма которого определяется приливными силами, предел Роша увеличивается почти в 2 раза:
- aR≈2,44R(ρMρm)13.{\displaystyle a_{R}\approx 2{,}44\,R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}.}
Более точно, учитывая несферичность центрального тела и массу спутника,
- aR≈2,423R(ρMρm)13((1+m3M)+c3R(1+mM)1−cR)13,{\displaystyle a_{R}\approx 2{,}423\,R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}\left({\frac {\left(1+{\frac {m}{3M}}\right)+{\frac {c}{3R}}\left(1+{\frac {m}{M}}\right)}{1-{\frac {c}{R}}}}\right)^{1/3},}
где c — разность радиусов центрального тела на экваторе и полюсе.
Объяснение
Комета Шумейкера-Леви 9 распалась под воздействием приливных сил Юпитера на цепочку более мелких тел в 1992 году, а затем столкнулась с планетой в 1994 году.
Предел Роша обычно применяется к распаду спутника из-за приливных сил, вызванных его основным телом, вокруг которого он вращается . Части спутника, расположенные ближе к первичной обмотке, сильнее притягиваются гравитацией от первичной обмотки, чем части, расположенные дальше; это несоответствие эффективно отделяет ближнюю и дальнюю части спутника друг от друга, и если несоответствие (в сочетании с любыми центробежными эффектами из-за вращения объекта) превышает силу тяжести, удерживающую спутник вместе, оно может тянуть спутник отдельно. Некоторые настоящие спутники, как естественные, так и искусственные , могут вращаться в пределах своих границ Роша, потому что они удерживаются вместе силами, отличными от гравитации. Объекты, лежащие на поверхности такого спутника, будут подниматься приливными силами. Более слабый спутник, такой как комета , может быть разбит, когда он пройдет в пределах своего предела Роша.
Поскольку в пределах предела Роша приливные силы подавляют гравитационные силы, которые в противном случае могли бы удерживать спутник вместе, ни один спутник не может гравитационно объединиться из более мелких частиц в этом пределе. Действительно, почти все известные планетные кольца находятся в пределах своего предела Роша. (Известные исключения Сатурн и . Эти два кольца могли бы быть остатками от прото-планетарной планеты аккреционного диска , который не сконцентрирован в moonlets, или , наоборот , которые образуются , когда луна прошла в пределах своего предела Roche и распалась. )
Предел Роша — не единственный фактор, который заставляет кометы распадаться. Расщепление под действием теплового напряжения , внутреннего давления газа и вращательное расщепление — это еще один способ расщепления кометы под действием напряжения.
Предел Роше и люди
Нам могут задать вопрос: почему наша планета не разрушает нас своей гравитацией, учитывая, что мы находимся в пределах границ Роша? Хотя возможно, что это могло быть логично, у него есть довольно простой ответ. Гравитация удерживает тела всех живых существ на поверхности планеты.
Этот эффект вряд ли имеет смысл по сравнению с химическими связями, которые скрепляют тело как единое целое. Например, эта сила, поддерживаемая химическими связями в нашем теле, намного сильнее силы тяжести. Фактически, гравитация — одна из самых слабых сил среди всех сил во Вселенной. Необходима точка, в которой гравитация действует интенсивно, например, в черная дыра как будто для того, чтобы предел Роша смог преодолеть силы, скрепляющие наши тела.
Я надеюсь, что с этой информацией вы сможете больше узнать о пределе Роша.
Избранные примеры
В таблице ниже показаны средняя плотность и экваториальный радиус для выбранных объектов в Солнечная система.[нужна цитата ]
| Начальный | Плотность (кг / м3) | Радиус (м) |
|---|---|---|
| солнце | 1,408 | 696,000,000 |
| земной шар | 5,513 | 6,378,137 |
| Луна | 3,346 | 1,737,100 |
| Юпитер | 1,326 | 71,493,000 |
| Сатурн | 687 | 60,267,000 |
| Уран | 1,318 | 25,557,000 |
| Нептун | 1,638 | 24,766,000 |
Уравнения для пределов Роша связывают минимальный устойчивый радиус орбиты с отношением плотностей двух объектов и радиуса основного тела. Следовательно, используя приведенные выше данные, можно рассчитать пределы Роша для этих объектов
Это было проделано дважды для каждого из них, принимая во внимание крайности случаев жесткого и жидкого тела. Средняя плотность кометы принимается около 500 кг / м3
В таблице ниже приведены пределы Роша, выраженные в километрах и первичных радиусах.[нужна цитата ] В можно сравнить с пределами Роша. Для удобства в таблице указан средний радиус орбиты для каждой, исключая кометы, орбиты которых чрезвычайно изменчивы и эксцентричны.
| Тело | спутник | Предел Роша (жесткий) | Предел Роша (жидкость) | Средний радиус орбиты (км) | ||
|---|---|---|---|---|---|---|
| Расстояние (км) | р | Расстояние (км) | р | |||
| земной шар | Луна | 9,492 | 1.49 | 18,381 | 2.88 | 384,399 |
| земной шар | средняя комета | 17,887 | 2.80 | 34,638 | 5.43 | Нет данных |
| солнце | земной шар | 556,397 | 0.80 | 1,077,467 | 1.55 | 149,597,890 |
| солнце | Юпитер | 894,677 | 1.29 | 1,732,549 | 2.49 | 778,412,010 |
| солнце | Луна | 657,161 | 0.94 | 1,272,598 | 1.83 | 149 597 890 приблизительно |
| солнце | средняя комета | 1,238,390 | 1.78 | 2,398,152 | 3.45 | Нет данных |
Эти тела выходят далеко за пределы Роша по разным причинам: от 21 для Луны (выше ее предела Роша с жидким телом) как части системы Земля-Луна до сотен для Земли и Юпитера.
В приведенной ниже таблице указаны значения максимального сближения каждого спутника на его орбите, разделенные на его собственный предел Роша. Опять же, даны расчеты как твердых, так и жидких тел
Обратите внимание, что Сковорода, Корделия и Наяда, в частности, могут быть довольно близки к их фактическим точкам разрыва
На практике плотность большинства внутренних спутников планет-гигантов неизвестна. В этих случаях, показанных на курсив, вероятные значения были приняты, но их действительный Предел Рош может отличаться от указанного значения.
| Начальный | спутник | Радиус орбиты / предел Роша | |
|---|---|---|---|
| (жесткий) | (жидкость) | ||
| солнце | Меркурий | 104:1 | 54:1 |
| земной шар | Луна | 41:1 | 21:1 |
| Марс | Фобос | 172% | 89% |
| Деймос | 451% | 234% | |
| Юпитер | Метис | ~186% | ~94% |
| Адрастеа | ~188% | ~95% | |
| Амальтея | 175% | 88% | |
| Бытие | 254% | 128% | |
| Сатурн | Сковорода | 142% | 70% |
| Атлас | 156% | 78% | |
| Прометей | 162% | 80% | |
| Пандора | 167% | 83% | |
| Эпиметей | 200% | 99% | |
| Янус | 195% | 97% | |
| Уран | Корделия | ~154% | ~79% |
| Офелия | ~166% | ~86% | |
| Бьянка | ~183% | ~94% | |
| Cressida | ~191% | ~98% | |
| Дездемона | ~194% | ~100% | |
| Джульетта | ~199% | ~102% | |
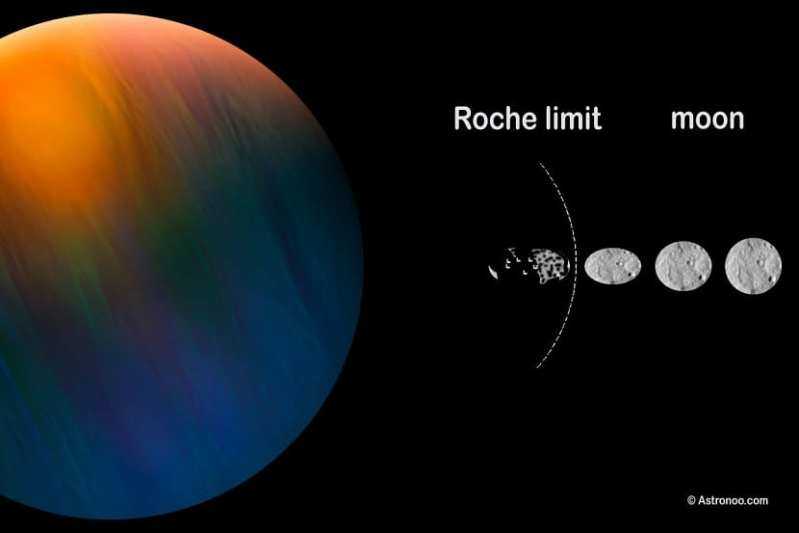
| Нептун | Наяда | ~139% | ~72% |
| Thalassa | ~145% | ~75% | |
| Деспина | ~152% | ~78% | |
| Галатея | 153% | 79% | |
| Лариса | ~218% | ~113% | |
| Плутон | Харон | 12.5:1 | 6.5:1 |
Предел Роша как геометрическая предельная форма
Трехмерное представление потенциала Роша двойной звездной системы с соотношением масс 2: 1, включая двумерную проекцию
Если звезда вращается вокруг партнера, она деформируется приливными силами. Если звезда достаточно большая и находится достаточно близко, она принимает форму слезы с острием, обращенным к партнеру. Если он находится в фазе расширения, например, в фазе перехода к красному гиганту , он не может расти дальше, но материал течет по этой вершине к партнеру. Эта форма капли также известна как предел Роша. Поскольку эта потеря массы снижает предел Роша (для формы конца круга), вся система может стать нестабильной, и звезда может полностью перетекать к своему партнеру.
Если партнер — компактный объект, такой как белый карлик , нейтронная звезда или черная дыра , во время переноса материала происходят драматические процессы. См. Новые и рентгеновские двойные звезды .
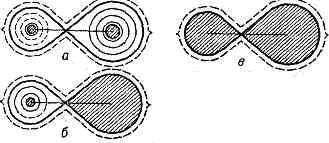
Предел Роша для всей системы состоит из двух эквипотенциальных поверхностей в форме капли, которые соприкасаются кончиками и, таким образом, образуют форму восьмерки. Этот наконечник представляет собой так называемую точку Лагранжа L 1 системы. Эта потенциальная поверхность должна быть рассчитана для совместно вращающейся системы координат . Это эффективный потенциал, который учитывает не только гравитационные, но и центробежные силы . Как только материал движется в этой системе, он также испытывает силы Кориолиса , которые можно описать только с помощью потенциала, зависящего от скорости.
Конкретные примеры
| Начальный | спутник | Расстояние (в радиусе Роша) | |
|---|---|---|---|
| (жесткий) | (жидкость) | ||
| солнце | Меркурий | 103,53 | 53,84 |
| земля | Луна | 40,53 | 21.08 |
| маршировать | Фобос | 1,71 | 0,89 |
| Деймос | 4,56 | 2.37 | |
| Юпитер | Метис | 1,91 | 0,99 |
| С зависимостью | 1,92 | 1,00 | |
| Амальтея | 1,78 | 0,93 | |
| Бытие | 3,31 | 1,72 | |
| Сатурн | Кастрюля | 1,77 | 0,92 |
| Атлас | 1,82 | 0,95 | |
| Прометей | 1,85 | 0,96 | |
| Пандора | 1,88 | 0,98 | |
| Эпиметей | 1,98 | 1.03 | |
| Уран | Корделия | 1,55 | 0,81 |
| Офелия | 1,68 | 0,87 | |
| Бьянка | 1,84 | 0,96 | |
| Cressida | 1,93 | 1,00 | |
| Нептун | Наяда | 1,44 | 0,75 |
| Thalassa | 1,49 | 0,78 | |
| Деспина | 1,57 | 0,82 | |
| Галатея | 1,84 | 0,96 | |
| Лариса | 2,19 | 1.14 | |
| Плутон | Харон | 13.05 | 6,79 |
На практике спутник — естественный или искусственный — может двигаться по орбите ниже предела Роша, потому что его удерживают другие силы сцепления. В таблице справа указаны радиусы орбит внутренних спутников каждой планеты, выраженные как кратные их соответствующих пределов Роша. Ртуть также включена для сравнения. Мы видим, что Найаде — самый крайний случай.
Все эти луны (кроме Луны и Харона ) остаются целыми, даже если они вращаются ниже или очень близко к пределу Роша.
Было замечено, что на Фобосе , спутнике Марса , есть многочисленные трещины, но невозможно объяснить их близостью к планете.
Теории создания планетных колец обычно включают предел Роша. Считается, что они создаются либо распадом спутника после того, как он прошел ниже предела, либо предотвращением агрегации частиц, находящихся в этой области, во время создания планеты. В случае колец Юпитера возможно, что они исходят непосредственно от частиц, оторванных от Адрасти и Метиса : приливных сил, исходящих от Юпитера, было бы достаточно для того, чтобы частица, помещенная на их поверхность, унеслась .
Кольцо E Сатурна выходит далеко за пределы орбиты Роша. Его необычная толщина предполагает, что это было результатом недавней вулканической дегазации Энцелада , кристаллы льда, таким образом, вызывали все большее и большее рассеяние по мере удаления от спутника.
Если бы луна подошла ближе к нашей планете
Прежде всего, следует отметить, что это полная фикция. Луна не может приблизиться к нашей планете, так что это все предположение. Фактически, в действительности Луна будет продолжать удаляться от Земли каждый год. Вернемся в то время, когда наша планета еще только формировалась, а орбита, на которой находился наш спутник, была ближе, чем нынешняя. В это время расстояние между планетой и спутником было меньше. Кроме того, Земля вращалась вокруг себя быстрее. Дни длились всего шесть часов, а Луна совершила оборот по орбите всего за 17 дней.
Сохранение углового момента важно поддерживать в обоих направлениях. Если Луне требуется больше суток для обращения по орбите, эффект будет таким же, как мы видим здесь
То есть вращение планеты замедляется, и спутник удаляется, чтобы это компенсировать. Однако, если Луна вращается быстрее сама по себе, это произведет противоположный эффект: вращение планеты ускорится, дни будут длиться меньше, а спутник станет еще ближе, чтобы компенсировать это.
РОША ПРЕДЕЛ
Теория приливного разрушения тел позволяет, в частности, объяснить наличиеблизко расположенных (двойных) кратеров на современных поверхностях Земли,
Смотреть что такое «РОША ПРЕДЕЛ» в других словарях:
Роша предел — Приближение «жидкого» спутника: на большом расстоянии от центрального тела форма спутника почти сферическая. При приближении к пределу Роша спутник деформируется приливными силами. На расстоянии, равном пределу Роша приливные силы и силы… … Википедия
Роша предел — критическое расстояние от планеты, ближе которого, вследствие разрушающего действия гравитационных сил, невозможно существование спутников. Исследован французским астрономом Э. Рошем (Е. Roche; 1820 83), установившим, что для жидких… … Большая советская энциклопедия
Предел Роша — Приближение «жидкого» спутника: на большом расстоянии от центрального тела форма спутника почти сферическая. При приближении к пределу Роша спутник деформируется приливными силами. На расстоянии, равном пределу Роша приливные силы и силы… … Википедия
Предел Чандрасекара — Предел Чандрасекара верхний предел массы, при котором звезда может существовать как белый карлик. Если масса звезды превышает этот предел, то она становится нейтронной звездой. Существование предела было доказано индийским астрофизиком… … Википедия
Сфера Хилла — Контурами изображены эффективные гравитационные потенциалы системы двух тел (на рисунке Солнце и Земля) и центробежные силы во вращающейся системе координат, в которой Земля и Солнце остаются неподвижны … Википедия
Рош, Эдуард Альберт — (фр. Édouard Albert Roche; 17 октября 1820, Монпелье 8 апреля 1883) французский астроном, математик, наиболее известный своими работами в области небесной механики. Содержание 1 Биография 2 Научная деятельность … Википедия
Эдуард Рош — Рош, Эдуард Альберт (фр. Édouard Albert Roche; 17 октября 1820, Монпелье 8 апреля 1883) французский астроном, математик, наиболее известный своими работами в области небесной механики. Содержание 1 Биография 2 Научная деятельность … Википедия
Рош, Эдуард Альбер — В Википедии есть статьи о других людях с такой фамилией, см. Рош (значения). Эдуард Альбер Рош фр. Édouard Albert Roche Дата рождения: 17 октября 1820(1820 10 17) … Википедия
ПУЛЬСАРЫ — переменные источники косм. эл. магн. излучения, открытые первоначально (1967, англ. учёный Э. Хьюиш с сотрудниками) как источники импульсного радиоизлучения с исключит. регулярно повторяющимися импульсами (рис. 1). Периоды повторения импульсов у… … Физическая энциклопедия
Белый карлик — У этого термина существуют и другие значения, см. Белый карлик (значения). Белые карлики проэволюционировавшие звёзды с массой, не превышающей предел Чандрасекара (максимальная масса, при которой звезда может существовать как белый карлик) … Википедия
Эффект гравитации и предел Роша
Точное расстояние, на которое спутник может приблизиться к своей планете, зависит от массы, размера и плотности обоих объектов. Например предел Роша, в случае с Землей и Луной, составляет 9500 километров. Если рассматривать Луну как идеальную твердую сферу. То есть если наш спутник будет находиться на расстоянии 9500 километров (или меньше) от Земли, гравитация нашей планеты преобладает над его собственной. Луна расколется и превратится в кольцо из фрагментов лунной породы, которые продолжат вращаться вокруг Земли, пока не упадут на ее поверхность. Подобное правило касается всех звезд, планет, астероидов и других космических объектов…
Например, если бы стандартная комета подошла к Земле ближе, чем на 18 000 километров, ее непременно разорвало бы на части. Солнце способно сделать то же самое на гораздо большем расстоянии — 1,3 миллиона километров. И это не просто теория. Разрушение спутников их планетами — это то, что реально происходит в Солнечной системе. Самым известным примером, несомненно, является Фобос. Он вращается вокруг Марса быстрее, чем планета вращается вокруг своей оси. И рано или поздно Фобос будет разрушен гравитацией Красной планеты.
Есть и еще один пример. Он не так хорошо известен, как предыдущий. Однако, возможно, он более впечатляющий. Из-за размера задействованных объектов. Это Тритон, крупнейший спутник Нептуна. В далеком будущем, примерно через 3,6 миллиарда лет, он достигнет предела Роша у своей планеты — Нептуна. И после этого возможно два варианта. Первый: Тритон устремится в атмосферу планеты, где и распадется. Второй: он будет разорван на части и превратится в систему колец, очень похожую на кольца Сатурна.
Очень возможно, что они у него так и появились.
Источник
Предел Роша в небесной механике и планетологии
Обычно следствием существования предела Роша называют тот факт, что спутники с нулевой собственной прочностью, обращающиеся на орбитах ниже предела Роша, неустойчивы и разрушаются приливными силами: примером такого разрушения может служить фрагментация кометы Шумейкеров — Леви-9 при её прохождении 7 июля 1992 года внутри предела Роша Юпитера.
Однако, гораздо более существенным для астрофизики и планетологии является «обратный» вывод: внутри сферы с радиусом, меньшим предела Роша, невозможна гравитационная конденсация вещества с образованием единого тела (спутника): кольца Сатурна расположены внутри предела Роша и состоят, судя по всему, из материи, сохранившейся с ранних стадий формирования Солнечной системы.
Общие сведения
Предел Роша (полость) – физическая область, без которой невозможно представить себе ни один крупный объект в космосе. Обычно в научном сообществе полость Роша тесно связывают с двойными звездами. В двойных системах вокруг каждой звезды-компаньона есть такая область, где силы ее притяжения преобладают над гравитационными силами другого компаньона. Эта область и называется полостью Роша. Названа она так в честь знаменитого французского астронома Эдуарда Альбера Роша.
Гравитационные силы звезды в области Роша преобладают не только над силой притяжения звезды-компаньона в двойной системе, но и над центробежной силой. Границы полости Роша определяет эквипотенциальная поверхность. Эта поверхность содержит внутри себя первую точку Лагранжа .
Дальнейший анализ
На графике гравитационного потенциала, L 1, L 2, L 3, L 4, L 5 находятся в синхронном вращении с системой. Области красного, оранжевого, желтого, зеленого, голубого и синего цветов — это потенциальные массивы от высокого к низкому. Красные стрелки — это вращение системы, а черные стрелки — относительные движения обломков.
Мусор движется быстрее в области с более низким потенциалом и медленнее в области с высоким потенциалом. Таким образом, относительное движение обломков на нижней орбите совпадает с направлением вращения системы, а на верхней орбите противоположно.
L1- точка равновесия гравитационного захвата. Это граница гравитации двойной звездной системы. Это минимальное потенциальное равновесие между L 1, L 2, L 3, L 4 и L 5 . Это самый простой способ перемещения обломков между сферой Хилла (внутренний круг синего и голубого цветов) и общими гравитационными областями (восьмерки желтого и зеленого цветов на внутренней стороне).
Сфера Хилла
L2и L 3 являются точками равновесия гравитационного возмущения. Проходя через эти две точки равновесия, обломки могут перемещаться между внешней областью (желтые и зеленые восьмерки на внешней стороне) и областью общей гравитации двойной системы.
L4и L 5 — максимальные потенциальные точки в системе. Это неустойчивые равновесия. Если соотношение масс двух звезд станет больше, то оранжевая, желтая и зеленая области станут подковообразной орбитой.
Красная область станет орбитой головастика.




![Глава 9. когда звезда у звезды крадет массу [1990 киппенхан р. - 100 миллиардов солнц: рождение, жизнь и смерть звезд]](http://site-edu.ru/wp-content/uploads/a/a/b/aab8aec6e0460d611b3d18cda2863962.jpeg)























