Планковская длина и объем

Введение

Физика входит в 21-й век с большим клубком нерешенных проблем. Если в конце 19-го века в физике было «все благополучно» за исключением отрицательных результатов опыта Майкельсона и непонятной зависимости излучения абсолютно черного тела от температуры, то к концу 20-го века физика накопила невиданное количество нерешенных проблем. Наиболее важные из них можно найти в недавно опубликованном В.Л. Гинзбургом списке 1999 года .

Если только две проблемы конца 19-го века привели к радикальному изменению ситуации в физике, то клубок нерешенных проблем конца 20-го века способен привести к обвальному пересмотру понимания устройства мира, за которым может последовать перекраивание сложившейся научной картины мира. Обилие неудачных попыток в создании новых физических теорий говорит о том, что правильное стратегическое направление исследований до сих пор не выявлено. Среди нерешенных фундаментальных проблем еще не обозначена та важнейшая проблема, решение которой даст ключ к решению других проблем. Усилия ученых направлены как на теоретические, так и на экспериментальные исследования. Поиск новых подходов активно проводится в области исследования новых физических полей на основе концепции физического вакуума. Для описания новых видов полей и новых взаимодействий необходимо проводить поиск констант взаимодействий. Весьма вероятно, что это должны быть новые еще неизвестные физике константы.

В настоящей работе затронута проблема, которая, на мой взгляд, незаслуженно выпала из поля зрения физиков и до сих пор не была обозначена в числе важнейших фундаментальных проблем. Я имею в виду проблему фундаментальных физических констант. Она должна стоять на первом месте, поскольку именно в ней содержится ключ к решению других проблем физики. Как будет показано ниже на некоторых примерах, эта проблема действительно является ключевой, а ее решение открывает большие возможности для поиска новых физических законов и новых физических констант.

Методы измерения[]

Использование законов фотоэффекта

При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:

Kmax=hν−A,{\displaystyle ~K_{max}=h\nu -A,}

где Kmax{\displaystyle ~K_{max}} — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,

ν{\displaystyle ~\nu } — частота падающего света,

A{\displaystyle ~A} — т. н. работа выхода электрона.

Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой ν1{\displaystyle ~\nu _{1}}, при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:

hν1=A+eU1,{\displaystyle ~h\nu _{1}=A+eU_{1},}

где e{\displaystyle ~e} — заряд электрона.

Затем тот же фотоэлемент облучают монохроматическим светом с частотой ν2{\displaystyle ~\nu _{2}} и точно также запирают его с помощью напряжения U2{\displaystyle ~U_{2}:}

hν2=A+eU2.{\displaystyle ~h\nu _{2}=A+eU_{2}.}

Почленно вычитая второе выражение из первого, получаем

h(ν1−ν2)=e(U1−U2),{\displaystyle ~h(\nu _{1}-\nu _{2})=e(U_{1}-U_{2}),}

откуда следует

h=e(U1−U2)(ν1−ν2).{\displaystyle ~h={\frac {e(U_{1}-U_{2})}{(\nu _{1}-\nu _{2})}}.}

Анализ спектра тормозного рентгеновского излучения

Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,

hcλ=eU,{\displaystyle ~h{\frac {c}{\lambda }}=eU,}

где c{\displaystyle ~c} — скорость света,

λ{\displaystyle ~\lambda } — длина волны рентгеновского излучения,

e{\displaystyle ~e} — заряд электрона,

U{\displaystyle ~U} — ускоряющее напряжение между электродами рентгеновской трубки.

Тогда постоянная Планка равна

h=λUec.{\displaystyle ~h={\frac {{\lambda }{Ue}}{c}}.}

Фундаментальная константа силы

Особенности констант физического вакуума привели к выводу, что силы взаимодействия также должны выражаться через константы вакуума. Покажем это. Из закона Кулона для взаимодействующих элементарных зарядов следует:

F = e2/l 2.

На основании формулы (8) представим это соотношение следующим образом:

F = h_uc/l 2 = h_uν2/c.

Значение h_u/c с учетом формулы (3) будет равно G_u. Исходя из этого, получим соотношение для закона универсального взаимодействия :

F = G_u·ν2.

Для предельного значения метрики из закона универсального взаимодействия получим следующее соотношение для константы силы:

F_u = h_u/l_ut_u.

Эта новая физическая константа названа фундаментальной константой силы. Ее значение равно:

F_u = 29,0535047(31) Н.

Она является универсальной константой силы для всех известных на сегодня видов взаимодействий. Как показано в , эта константа присутствует не только в законе Кулона, но и в законах Ньютона, в законе Галилея, в законе Ампера и в законе всемирного тяготения.

Физический смысл[]

В квантовой механике импульс имеет физический смысл волнового вектора, энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах (кг·м/с, Дж, Дж·с), чем соответствующие волновые (м−1, с−1, безразмерные единицы фазы). Постоянная Планка играет роль переводного коэффициента (всегда одного и того же), связывающего эти две системы единиц — квантовую и традиционную:

p=ℏk{\displaystyle \mathbf {p} =\hbar \mathbf {k} } (импульс) (|p|=2πℏλ){\displaystyle (|\mathbf {p} |=2\pi \hbar /\lambda )}

E=ℏω{\displaystyle E=\hbar \omega } (энергия)

S=ℏϕ{\displaystyle S=\hbar \phi } (действие)

Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с ℏ=1{\displaystyle \hbar =1}, в ней

p=k{\displaystyle \mathbf {p} =\mathbf {k} } (|p|=2πλ){\displaystyle (|\mathbf {p} |=2\pi /\lambda )}

E=ω{\displaystyle ~E=\omega }

S=ϕ{\displaystyle ~S=\phi }

(ℏ=1){\displaystyle (\hbar =1)}.

Постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики: она в сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, показывает, насколько применима к данной физической системе классическая механика. А именно, если S{\displaystyle ~S} — действие системы, а M{\displaystyle ~M} — её момент импульса, то при Sℏ≫1{\displaystyle ~{\frac {S}{\hbar }}\gg 1} или Mℏ≫1{\displaystyle ~{\frac {M}{\hbar }}\gg 1} поведение системы с хорошей точностью описывается классической механикой. Эти оценки достаточно прямо связаны с соотношениями неопределенностей Гейзенберга.

Планковские величины

Эти величины были обнародованы Планком 18 мая 1899 года. Учёный предложил систему «естественных единиц измерений», которая была основана на четырёх универсальных постоянных:

Скорость света
Гравитационная постоянная
Постоянная Планка
Постоянная Больцмана

Планковская длина

В Международной системе единиц (СИ) значение такого параметра определено примерно в 1,6 . 10-35 м. В эту естественную единицу вошли фундаментальные константы: скорость света, постоянная Планка, гравитационная постоянная. Наблюдаемая Вселенная имеет приблизительный радиус, равный 4,6 .1061 планковских длин.

Измерение объектов с точностью, превосходящей длину системы единиц Планка, невозможно, поэтому представления о пространстве на меньших расстояниях неприменимы. По такой же причине нереально обнаружить дополнительные измерения, которые наличествуют в теории струн, так как они свёрнуты до параметров таких длин. Планковская длина считается предельным значением расстояния. Ниже этого предела само понятие длины перестаёт существовать, впрочем, как и пространство.

Планковское время

Эта единица имеет размерность времени и состоит из произведения фундаментальных констант. В физическом смысле – это время, необходимое частице, двигающейся со скоростью света, на преодоление планковской длины. Результатом Большого взрыва стало расширение пространства-времени из бесконечно малой точки. По прошествии одной такой единицы времени, гравитационные силы начинают отделяться от всех остальных сил. То время, что прошло после Большого взрыва, определяется в параметре 4,3 . 1017 с, что равно 8 .1060 планковских времён. На нынешний момент минимальный отрезок времени, доступный наблюдению, составил около аттосекунды, или 1026 величин времени Планка.

Планковская температура

Для современной физической теории невозможна величина температуры выше планковского значения. При параметрах больших энергия частиц увеличивается так сильно, что связывающие их силы сравниваются с остальными взаимодействиями. Такую температуру имела Вселенная в планковское время после Большого взрыва. Значение её непредставимо – 1,41679(11) . 1032 К (141 нониллион 679 октиллионов кельвинов).

Планковская масса

Планковская масса — величина минимальной массы чёрной дыры или максимально тяжелой элементарной частицы. Эта величина выделяется из других единиц Планка тем, что масштаб её более понятен. Поскольку значение её 2,176 . 10-8 кг (дли физики элементарных частиц – 2,43 . 1018 ГэВ/с2), она подходит для взвешивания ощутимых объектов. Например, блоха будет иметь массу в пределах от 4000 до 5000 планковских масс. Предложена гипотетическая частица, наделённая подобной массой – максимон. Такие частицы могут обладать электрическим зарядом, а могут оставаться нейтральными. Внутренняя температура их может быть предельно большой, или же они могут оставаться холодными.

Планковский заряд

Эта единица является одной из основных в планковской системе. Она выражается количеством электрического заряда, который определён терминами фундаментальных констант. Значение этой единицы 1,87554 . 10-18 кулон. Этот заряд по модулю превышает заряд электрона примерно в 11,706 раза.

Планковская плотность

За единицу плотности в этой системе принята плотность Вселенной по завершении планковской эпохи после Большого взрыва. Величина этого параметра огромна. Она сопоставима с 1023 масс Солнца, которые сжали в пространстве до размера ядра атома. Это значение является предельной плотностью для материи.

Планковская длина и евклидова геометрия

Планк длина — длина, на которой квантовые нулевые колебания гравитационного поля полностью искажают евклидову геометрию. Гравитационное поле совершает нулевые колебания, и связанная с ним геометрия также колеблется. Отношение длины окружности к радиусу колеблется около евклидова значения. Чем меньше масштаб, тем больше отклонения от евклидовой геометрии. Оценим порядок длины волны нулевых гравитационных колебаний, при которой геометрия становится совершенно непохожей на геометрию Евклида. Степень отклонения ζ {\ displaystyle \ zeta}геометрии от евклидовой геометрии в гравитационном поле определяется соотношением гравитационного потенциала φ {\ displaystyle \ varphi}и квадрат скорости света c {\ displaystyle c}: ζ = φ / c 2 {\ displaystyle \ zeta = \ varphi / c ^ {2}}. Когда ζ ≪ 1 {\ displaystyle \ zeta \ ll 1}, геометрия близка к геометрии Евклида; для ζ ∼ 1 {\ displaystyle \ zeta \ sim 1}все сходства исчезают. Энергия колебания шкалы l {\ displaystyle l}равна E = ℏ ν ∼ ℏ c / l {\ displaystyle E = \ hbar \ nu \ sim \ hbar c / l}(где c / l {\ displaystyle c / l}- порядок частоты колебаний). гравитационный потенциал, создаваемый массой m {\ displaystyle m}, на этой длине φ = G m / l {\ displaystyle \ varphi = Gm / l}, где G {\ displaystyle G}- постоянная всемирной гравитации. Вместо m {\ displaystyle m}мы должны подставить массу, которая, согласно формуле Эйнштейна, соответствует энергии E {\ displaystyle E}(где m = E / c 2 {\ displaystyle m = E / c ^ {2}}). Получаем φ = GE / lc 2 = G ℏ / l 2 c {\ displaystyle \ varphi = GE / l \, c ^ {2} = G \ hbar / l ^ {2} c}. Разделив это выражение на c 2 {\ displaystyle c ^ {2}}, мы получим значение отклонения ζ = G ℏ / c 3 l 2 = ℓ P 2 / l 2 {\ displaystyle \ zeta = G \ hbar / c ^ {3} l ^ {2} = \ ell _ {P} ^ {2} / l ^ {2}}. Приравнивая ζ = 1 {\ displaystyle \ zeta = 1}, мы находим длину, при которой евклидова геометрия полностью искажается. Она равна планковской длине ℓ P = G ℏ / c 3 ≈ 10 — 35 м {\ textstyle \ ell _ {P} = {\ sqrt {G \ hbar / c ^ {3}}} \ приблизительно 10 ^ {- 35} \ mathrm {m}}.

Как отмечалось в Редже (1958) «для области пространства-времени с размерами l {\ displaystyle l}неопределенность символы Кристоффеля Δ Γ {\ displaystyle \ Delta \ Gamma}иметь порядок ℓ P 2 / l 3 {\ displaystyle \ ell _ {P} ^ {2} / l ^ {3}}, а неопределенность метрического тензора Δ g {\ displaystyle \ Delta g}составляет порядок ℓ P 2 / l 2 {\ displaystyle \ ell _ {P} ^ {2} / l ^ {2}}. Если l {\ displaystyle l}- макроскопическая длина, квантовые ограничения фантастически малы, и ими можно пренебречь даже в атомных масштабах. Если значение l {\ displaystyle l}сравнимо с ℓ P {\ displaystyle \ ell _ {P}}, тогда сохранение прежнего (обычного) представления о пространстве становится все более и более трудным, и влияние микрокривизны становится очевидно «. Предположительно, это может означать, что пространство-время становится квантовой пеной в масштабе Планка.

Новое значение константы G

Зависимость константы Gот первичных суперконстант указывает на то, что эту важнейшую постоянную можно получить посредством математических расчетов. Как известно, сама форма закона всемирного тяготения Ньютона – прямая пропорциональность силы массам и обратная пропорциональность квадрату расстояния, проверена с гораздо большей точностью, чем точность определения гравитационной постоянной G. Поэтому, основное ограничение на точное определение гравитационных сил накладывает константа G. Кроме того, со времен Ньютона остается открытым вопрос о природе гравитации и о сущности самой гравитационной постоянной G. Эта константа определена экспериментально. Науке пока неизвестно существует ли аналитическое соотношение для определения гравитационной константы. Науке также не была известна связь между постоянной Gи другими фундаментальными физическими константами. В теоретической физике эту важнейшую постоянную пытаются использовать совместно с постоянной Планка и скоростью света для создания квантовой теории гравитации и для разработки единых теорий. Поэтому, вопросы о первичности и независимости константы G, а также необходимость знать ее точное значение, выходят на первый план.

Численное значение G было определено впервые английским физиком Г. Кавендишем в 1798 г. на крутильных весах путем измерения силы притяжения между двумя шарами.

Современное значение константы G, рекомендуемое CODATA 1998 :

G = 6,673(10)·10–11 м3кг–1с–2.

Из всех универсальных физических постоянных точность в определении G является самой низкой. Среднеквадратическая погрешность для G на несколько порядков превышает погрешность других констант.

Совершенно неожиданным оказалось то, что G может быть выражена посредством электромагнитных констант. Это становится важным, так как точность констант электромагнетизма намного больше точности постоянной G.

Открытая группа универсальных суперконстант, имеющих первичный статус, и выявленная глобальная связь фундаментальных констант позволили получить математические формулы для вычисления гравитационной постоянной G . Таких формул оказалось несколько. В качестве подтверждения этому, ниже приведены 9 эквивалентных формул:

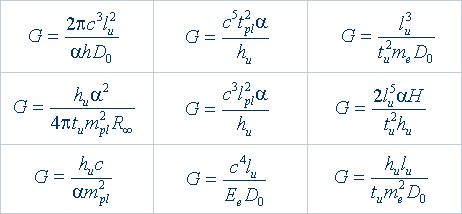
Из приведенных формул видно, что константа G выражается с помощью других фундаментальных констант очень компактными и красивыми соотношениями. При этом, все формулы для гравитационной константы сохраняют когерентность. В числе физических постоянных, с помощью которых представлена гравитационная константа, находятся такие константы как фундаментальный квант h_u, скорость света c, постоянная тонкой структуры α, постоянная Планка h, число π, фундаментальная метрика пространства-времени (l_u, t_u), элементарная масса m_e, элементарный заряд e, большое число Дирака D, энергия покоя электрона E_e, планковскиеединицы длины l_pl, массы m_pl, времени t_pl, постоянная Хаббла H, константа Ридберга R_∞. Это указывает на единую сущность электромагнетизма и гравитации и на наличие фундаментального единства у всех физических констант. Из приведенных формул видно, что связь между электромагнетизмом и гравитацией действительно существует и проявляется даже на уровне гравитационной константы G.

Теперь, по прошествии 200 лет после первого измерения G, появилась возможность на основе полученных формул вычислить ее точное значение, используя константы электромагнетизма. Поскольку точность в определении констант электромагнетизма высокая, то точность гравитационной постоянной можно приблизить к точности электромагнитных констант. Все приведенные выше формулы дают новое значение G, которое по точности почти на пять порядков (!) выше известного на сегодня значения. Новое значение G вместо четырех цифр содержит 9 цифр :

G = 6,67286742(94)·10–11 м3кг–1с–2.

С помощью универсальных суперконстант удалось получить новые формулы для планковских констант :

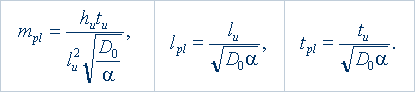
На основе этих формул получены новые значения планковских констант:

m_pl = 2,17666772(25)·10–8 кг.

l_pl = 1,616081388(51)·10–35 м.

t_pl = 5,39066726(17)·10–44 с.

Эти новые значения планковских констант по точности почти на пять порядков точнее известных на сегодня значений .

Универсальные суперконстанты позволили получить новое точное значение параметра Хаббла:

H = 53,98561(87) (км/с)/Мпс.

История открытия[]

Формула Планка для теплового излучения

Основная статья: Формула Планка

Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения u(ω,T){\displaystyle u(\omega ,T)}. Формула Планка была получена после того, как стало ясно, что формула Рэлея — Джинса удовлетворительно описывает излучение только в области длинных волн. В 1900 году Планк предложил формулу с постоянной (впоследствии названной постоянной Планка), которая хорошо согласовывалась с экспериментальными данными. При этом Планк полагал, что данная формула является всего лишь удачным математическим трюком, но не имеет физического смысла. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения выражением:

ε=ℏω.{\displaystyle \varepsilon =\hbar \omega .}

Коэффициент пропорциональности ℏ{\displaystyle \hbar } впоследствии назвали постоянной Планка, ℏ{\displaystyle \hbar } = 1.054×10−34 Дж·с.

Фотоэффект

Основная статья: Фотоэффект

Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.

Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:

ℏω=Aout+mv22{\displaystyle \hbar \omega =A_{out}+{\frac {mv^{2}}{2}}} В этом случае неправильно определена кинетическая энергия электрона, так как он имеет начальную скорость движения Е = m( V +Δv)^2 / 2, где Δv — величина на которую увеличилась скорость движения электрона под действием n импульсов излучений. Разность кинетических энергий электрона равна ΔЕ = mVΔv + mΔv^2 / 2. Из этого следует, что постоянная Планка по расчётам Эйнштейна не срртветствует действительности.

Вторая ошибка Эйштейна заключается в том, что энергия кванта излучения hυ- есть энергия излучения за 1 сек., так как υ- есть количество волн излучения за 1 сек.. Считать в этом случае квант излучения одной частицей «фотоном» не возможно, так как его масса равномерно распределена на расстоянии 300000000 м. Из формулы разности кинетических энергий электрона видим, что энергия изиеняется по квадратичной зависимости, а по формуле планка энергия излучения определяется по линейной зависимости Е = h υ. Таким образом постоянная Планка определена с ошибкой.

где Aout{\displaystyle A_{out}} — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), mv22{\displaystyle {\frac {mv^{2}}{2}}} — кинетическая энергия вылетающего электрона, ω{\displaystyle \omega } — частота падающего фотона с энергией ℏω{\displaystyle \hbar \omega }, ℏ{\displaystyle \hbar } — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже не достаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества, то есть на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.

Измерение длины

Планковская длина накладывает ограничение на возможность измерения длины. То есть если передвинуть любой объект на одну планковскую длину (или меньше) в сторону, то отследить изменение его положения не предоставляется возможным.

Дело в том, что для определения положения любого тела следует «пустить» в его сторону поток электромагнитного излучения, фотонов, после чего он возвратится на датчики измерительных приборов. Точность такого измерения будет зависеть от длины волны этого излучения. Тогда чтобы отследить изменение положения тела порядка планковской длины, потребуется электромагнитная волна длиной не больше планковской длины. С уменьшением длины волны излучения возрастает энергия фотонов. С упомянутой же длиной волны энергия фотонов была бы настолько велика, что они сколлапсировали бы в маленькие черные дыры, что не позволило бы провести измерение.

То есть, как и некоторые другие планковские величины, планковская длина является нижним пределом расстояния, на котором действуют известные нам физические законы, излагаемые общей теорией относительности и квантовой физикой. Нажмите кнопку СТАРТ и откройте для себя новый, неизведанный мир!